Keywords
|
| ECONOMIC LOAD DISPATCH, PARTICLE SWARM OPTIMIZATION, TRANSMISSION LOSS, UNIT COMMITMENT |
INTRODUCTION
|
| Power System which is capable of feeding a bounded range of electrical load demand, optimizing the operation costs of the generation units is very important from an Economic Dispatch perspective. Hence, usually economic Dispatch(ED) techniques are used to determine a condition with the lowest possible generation costs. The load demand, transmission power losses and generation cost coefficients are the parameters must be taken into account for any ED technique .The modern generation units present non-linear behaviors with multiple local optima in their input-output characteristics. Therefore, the economic dispatch problem formulation shall be discontinues, multi model and extremely non-linear. |
| During the past decade, many efforts have been focused toward solving the Ed problem, incorporating different kinds of constraints through the various mathematical programming and optimization techniques. The conventional methods include lambda iteration method, gradient method, etc. However, these classical dispatch algorithms require the incremental cost curves to be monotonically increasing or piece-wise linear and are highly sensitive in the starting point and frequently converge to local optimum solution or diverge altogether .Newton based algorithms have a problem in handling a large number of inequality constraints. Linear programming methods are fast and reliable, but the main disadvantage is associated with the piecewise linear cost approximation .Nonlinear programming methods have a problem of convergence and algorithm complexity. |
PROBLEM FORMULATION
|
| The Economic Dispatch (ED) is a nonlinear programming problem which is considered as a sub – problem of the unit commitment (UC) problem. In a specific power system with a determined load schedule, ED planning performs the optimal power generation dispatch among the exiting generation units. The solution of ED problem must satisfy the constraints of the generation units, while it optimizes the generation based on the cost factors of the generation units. Equation represents the total fuel cost for a power system which is the equal summation of all generation units fuel cost, in a power |
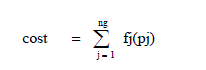 |
| where n g = the number of generation units, P j = the output power of j th generation units. The cost function in approximated to a quadratic function of the power generation, therefore, the total cost function will be changed. |
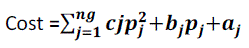 |
| where pj= generation power by jth generation units; aj , bj , cj = fuel cost co efficient of unit j. |
SYSTEM CONSTRAINTS
|
| A. Equality Constraints |
| Normally, in a power system the amount of generated power as to be enough to feed the load demand plus transmission lines losses. Since the transmission lines are located between the generating units and loads, P loss can occur anywhere before the power reaches load (pd). Any shortage in the generated power will cause shortage in feeding the load demand which may cause many problems for the system and loads. |
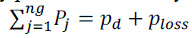 |
| where pd = the load demand; P loss= The Transmission line loss; ng = The number of generation units; pj = The output power of jth generation units |
| Here , the loss co- efficient method which is developed by Kron and Kirchmayer , is used to include the effect of transmission losses .B matrix which is known as the transmission loss co-efficient matrix is a square matrix which a dimension of ng*ng , While ng = the number of generation unit in the system . |
| Applying B matrix gives a solution with generated powers of different units as the variables. Equation (4) shows the function of calculating P loss as the transmission loss through B matrix. |
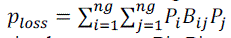 |
| where P loss = total transmission loss in the system; Pi, Pj = the generated power by ith and jth generating unit respectively; Bij= the element of the B matrix between ith and jth generating units. |
| B. In Equality Constraints |
| All generation units have some limitations in output power regardless of the types. In exiting power systems, the thermal units play a very important role .Thermal units can be pose both maximum and minimum constraints on the generating powers so there is always a range of operating work for the generating units .Generating less power than minimum may cause the rotor to over speed whereas at maximum power, it may cause in stability issues for synchronous generators. So as to be considered in all steps of solving the ED problem. |
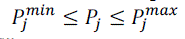 |
| For j = 1, 2…ng .Where Pjmin and Pjmax are the constraints of generation for jth generating unit. |
PARTICLE SWARM OPTIMIZATION
|
| Particle swarm optimization (PSO) is a population based stochastic optimization technique developed by Dr.Ebehart and Dr. Kennedy in 1995, inspired by social behaviour of bird flocking or fish schooling. PSO simulates the behaviors of bird flocking. Suppose the following scenario: a group of birds are randomly searching food in an area. There is only one piece of food in the area being searched. All the birds do not know where the food is. But they know how far the food is in each iteration. So what's the best strategy to find the food? The effective one is to follow the bird, which is nearest to the food. PSO learned from the scenario and used it to solve the optimization problems. In PSO, each single solution is a "bird" in the search space. We call it "particle". |
| All the particles have fitness values, which are evaluated by the fitness function to be optimized, and have velocities, which direct the flying of the particles. The particles fly through the problem space by following the current optimum particles. PSO is initialized with a group of random particles (solutions) and then searches for optima by updating generations. In every iteration, each particle is updated by following two "best" values. The first one is the best solution (fitness) it has achieved so far. (The fitness value is also stored.). This value is called “pbest”. Another "best" value that is tracked by the particle swarm optimizer is the best value, obtained so far by any particle in the population. This best value is a global best and called “gbest”. When a particle takes part of the population as its topological neighbours, the best |
| value is a local best and is called p-best. After finding the two best values, the particle updates its velocity and positions with following. |
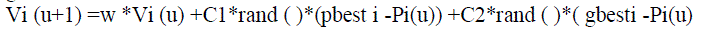 |
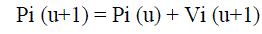 |
| In the above equation, the term rand ( )*(pbest i –Pi (u)) is called particle memory influence. The term rand ( )*( gbesti -Pi(u)) is called swarm influence. Vi (u) which is the velocity of ith particle at iteration ‘u’ must lie in the range Vmin ≤ Vi (u) ≤ Vmax . The parameter Vmax determines the resolution, or fitness, with which regions are to be searched between the present position and the target position. If Vmax is too high, particles may fly past good solutions. If Vmin is too small, particles may not explore sufficiently beyond local solutions. In many experiences with PSO, Vmax was often set at 10-20% of the dynamic range on each dimension. The constants C1and C2 pull each particle towards pbest and gbest positions. Low values allow particles to roam far from the target regions before being tugged back. On the other hand, high values result in abrupt movement towards, or past, target regions. The acceleration constants C1 and C2 are often set to be 2.0 according to past experiences.Suitable selection of inertia weight ‘ω’ provides a balance between global and local explorations, thus requiring less iteration on average to find a sufficiently optimal solution. In general, the inertia weight w is set according to the following equation, |
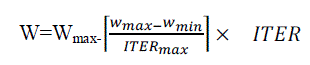 |
| where w -is the inertia weighting factor,Wmax - maximum value of weighting factor,Wmin - minimum value of weighting factor, ITERmax - maximum number of iterations and ITER - current number of iteration |
PROPOSED METHODOLOGY
|
| The current proposed PSO-based algorithm.is developed to obtain an efficient solution for an Economic Dispatch (ED) problem. The optimized solution will give the best amount of power generation for each generation unit in terms of costs. Some definitions are made in the proposed algorithm as follows. |
REPRESENTATION OF SWARM
|
| Swarm is the particles which are moving are moving and giving solutions for solving the problem. The particles move in the domain of the problem space and each of them represents a solution for the problem. Swarm is the particles which are moving and giving solutions for solving the problems .The particles move in the domain of the problem space and each of them represents a solution for the problem .ED problem. If P1, P2and P3 the generation units in a system, then particle (i) flies in the problem area to find the best possible solution. Vector vi is the resultant vector which is obtained from (6).For a system with more than three generation units, we cannot demonstrate them in a 2- D paper because there is no Cartesian space available. However, we can consider systems with more than three dimensions theoretically to solve problems. In the current study, arrays and matrixes are the problem search space. |
| A. Fitness Function |
| To evaluate the proposed solution by particles, we need to define a fitness function. The fitness function has to be able to determine which solution is better and more efficient after considering all the solutions obtained by the particles at every iteration. Normally the fitness function is being set to have the lowest possible value at an optimum point. In the current study, we also need to have the lowest possible value for the cost and transmission lost hence the fitness function is proposed as follows, |
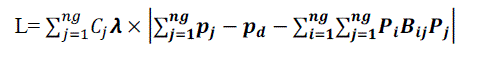 |
| where; L is the value of fitness function;cj is the cost function of generation units j;pd is the power demand by the loads ;λ is the coefficient of error ;Pi and pj is the generated power by ith and jth units respectively .The fitness function is generated by two parts Summation of cost and error in generation which is the difference between desired generation and real generation. The desired generation is the amount that can feed loss demand (Pd) and power transmission loss (4),but the real generation is the summation of units .if Those two numbers are not the same , the system will not work in an ideal situation and there will be a lack of feeding loads . In the best case, the absolute part in (9) will be zero, therefore we set λ to a high value to magnify any error .In this paper, the value of λ is equal to 100 and any small error will be mirrored in the value of the fitness function. |
| B. The Proposed algorithm of PSO |
| Here, an algorithm based on particles swarm optimization is proposed to give a quick solution solves economic dispatch problems. Unlike other PSO algorithm, in this method each single particle gives a solution to solve the main problem .In each generation of movement the best given solution by the particle is collected and that point in the problem space is called the global best .personal best is the point that any particle by itself has experienced so far. Although, these particles have the opportunity to search the full area of the problem space, missing some points in the problem space is inevitable because the vectors determine the direction of movement of each particle .Hence, getting close to global best point might hold the particles around that point. However , the detected global best point is not necessarily the optimum solution to the problem .To overcome this , the acceleration factors of global best and personal best which are known as C1 and C2 have been adapted in a manner that let the particles search the problem space easier and with more efficient . |
| The steps of the proposed algorithm are as shown below: |
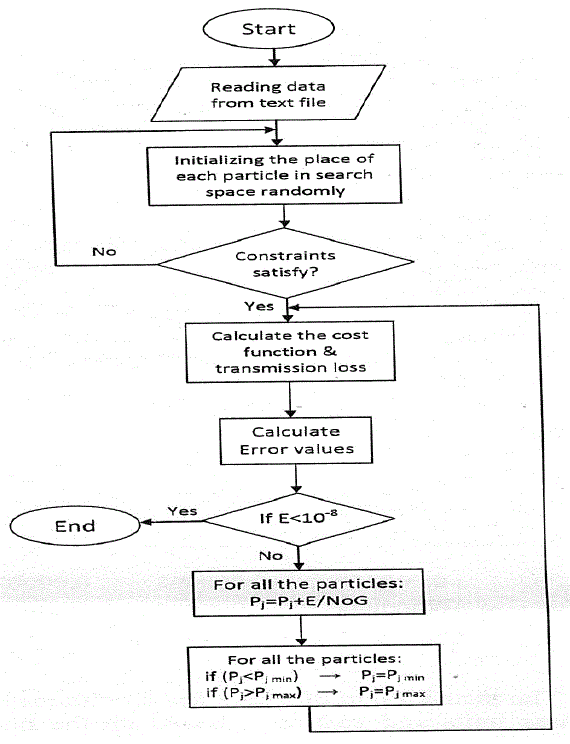
| Step: 1 Receive the data of generation units, characteristics, loss co-efficient matrix B, and load demand from a text file .Initialize the position for all the particles in the problem space randomly while the constraints of generation units are satisfied. X[i] [j] Holds the position of particles in problem space while, i- Indicates the particles, j- generation unit. Step: 2 Calculate the cost function (1) and transmission loss matrix Ploss (4) based on loss co- efficient matrix B for each particle that gives a solution for the problem. Then an error function is defined as a matrix to calculate the difference between the estimated power generation and summation of demand load Pd and Ploss as bellowed[i] = PG[i]-(Pd+Ploss[i]); (10)Then the value of error for each particles is divided among the number of generators to be shared between them .Step 2 is placed in a infinite for loop while the value of error is less than a small number and which has been considered equal to 0.00000001 in the current algorithm. |
| Step: 3 calculate the fitness function (9) based on the obtained the value for generation units from step 2. Note that for each particles one fitness values exceeds hence, we have a matrix with dimension equal to the number of particles called L[i] , Where ,i- Indicates the particles. |
| Step: 4 compare all the values of L [i] matrix to find the lowest value as the global best solution. This solution is saved in a matrix called gbest [j]While its dimension is 1*j and j –Number of generation Units .Since the movement part is not started yet , the personal best value of each particles is set to its current location and saved in a matrix Pbest [i][j]. |
| Step: 5 Movement part Modify the initial velocity of each particle based on (10) |
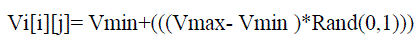 |
| ,i=1,2,………,nop(thenumberofparticles),j=1,2………,nod(numberof dimension)While the number of dimension demonstrates the number of generation units |
| Step: 6 A for loop which determined the number of iteration starts from this steps. The particle starts by renewing the velocity of each particle based on equation (11) |
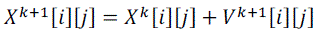 |
| i= 1,2,………, nop (the number of particles ) j- 1,2………, nod (number of dimension)Where i and j have same definition as in step 5 rl and r2 are random numbers between 0 and 1, W is the inertia weight of velocity which is obtained by (8) ,and are specification of particle , i- at iteration k, c1and c2 are the global best acceleration factor and personal best acceleration factor and personal best of freedom in searching the problem space. Calculating the new location of each particle of movement at iteration k+1 is the next aim of this step which is obtained through. |
| Step: 7 Check the values of Xk =1[i][j] matrix to make sure no generation unit violates its constraints. If Xk+1[i][j] is not in range the value will be set to either minimum when X<Pmin or maximum when X> P max . |
| Step: 8 Calculate the cost function (1),Ploss is based on coefficient matrix (4) and value of fitness function matrix (9).Compare all valves of Lk=1[i]as the fitness matrix at iteration K=1 to find the global best and then save the solution in gbest[j].The number of particle which generates gbest[j]is saved as a number called OP means optimum particle. Compare the current fitness value at iteration K through matrix L[i]. If the fitness value of any particle has decreased, the better solution would be replaced with former solution in matrix pbest [i][j]which holds the best solution for each single particle. |
| Step 9: If the number of iteration reaches its maximum, then go to step 10. Otherwise, go to step 6. |
| Step 10: Here gbest [j]is the best solution of the problem while j indicates the number of generation Units. Also the particle which made the best solution has been saved in Op and can be obtained. Then by referring to the cost function which values are registered in cost[i][j]matrix, cost[OP][j]holds the cost of all generation values. |
RESULTS AND DISCUSSION
|
| Here, the results of four different case studies have been brought to verify the feasibility of the proposed PSO algorithm. In these cases, the obtained results are compared to existing PSO based and GA based results .At each case, under the same function of operation and algorithm, we performed 10 trials to make sure that the solution is not stammered in any local optimum point. Considering the transmission lines power losses and the transmission capacity constraints, a reasonable B loss coefficients matrix has been utilized processor, personalcomputerwith4.00GB RAM. The programming was in C language and executed on an AMD. PSO method seems to be sensitive to the variation of weights and factors; hence in the present study different factors and parameters can affect the swarm performance. However, the results presented only belong to the best set of parameters which leads the swarm to the optimum place. |
| A. Case study 1 |
| Example 1 Three –Unit System: this case study has been adapted from which is considering as a small system containing three thermal units .The system has the load demand of 150 MW. Table 1 shows the cost characteristics of three generators while matrix B is the loss coefficient matrix for the considered system. |
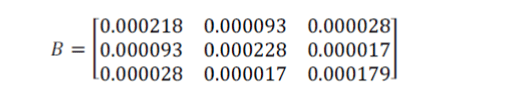 |
| The matrix Pg in their case has 3 column based on three units and 150 rows based on the number of particles which is constant for all four cases. A s it has been described the generation of P1, P2 and P3 are random and the dimension of the swarm is 150 x 3. The number of particles is normally assumed to be 100. But in the current study, the number has been increased to 150 to give the swarm more opportunity to search the problem space easier. However, for small cases we do not need many particles to find the optimum but in large scales, having a larger number of particle makes the swarm more capable to search the problem space faster and more reliable. The best results based on the proposed algorithm and existing results have been listed in Table 2. Figure 4 illustrates the convergence property of the proposed algorithm for example 1. |
| Results of Table 1 show an acceptable improvement in the total cost of the system which demonstrates the ability of the proposed algorithm even in a small problem search space. |
| B. Case Study 2 |
| Example 2 Six unit system: this system includes six thermal generation units with characteristics given in Table 3 (28) The system contains 26 buses and 46 transmission lines while the load demand is 1263 MW. Low coefficients B matrix of the system is as follows. : |
 |
| In this case P1, P2, P3, P4, P5, P6 generate the column of Pg as generation matrix while the number of particles indicates the row number; hence the dimension of pg is 150 x 6. Through the proposed algorithm the best solution of solving this problem are shown in Table 4. The obtained results satisfy the desired generating unit’s constraints. The convergence property of the algorithm is illustrated in Fig. 5. |
| Convergence Profile of Fitness Value shows that the proposed algorithm has more compared to GA based method and also the proposed PSO – base method |
Tables at a glance
|
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
Figures at a glance
|
 |
| Figure 1 |
|
References
|
- Jong-BaePark,Member,IEEE,Yun-Won Jeong,Joog-RinShin,SeniorMember,IEEE,KwangY.Lee,Fellow,IEEE,and Jin-HoKim,Member, “AHybrid Particle Swarm Optimization Employing Crossover Operation for Economic Dispatch Problems with Valve-point Effects ,“ IEEE1996
- Ching-Tzongsu,MemberGwo-Jen Chin,student Member ,“ A Fast-computation Hopfield Method To Economic Dispatch of Power Systems,”IEEE Transactions on Power Systems,Vol 12,NO.4,1997
- Young-Hyun Moon,Jeong-Do Park,Yong-HoonLee,Hyun-Jong Kook,Jong-Gi Lee,” A New Economic Dispatch Algorithm for Thermal UnitGeneration Scheduling in power System,’ ’IEEE o-7803-5935-6/00/$10.00(c)2000
- Jong-BaePark,Member,IEEE,Ki-Song Lee,Joong-RinShin,andKwangY.Lee,fellow,” A particle Swarm Optimization for Economic DispatchwithNonsmooth Cost Function,” IEEE Transaction on Power Systems,Vol.20,No.1,2005
- C.A.Roa-SepuluvedaB.J.Pavez- Lazo ,‘’ASoultion to the optimal power flow Using Simulated Annealing,” PPT 2001 IEEE porto Power Tech
- Zwe-Lee Gaing “Particle Swarm optimization to Solving the Economic Dispatch Considering the Generator Constraints,”IEEE Transaction onpower system,VoL.18,No.3,2003
- M.F.Alhajri and M.E.EL-Hawary,“Pattern Search Optimization Applied to convex and Non convex Economic Dispatch,”1-4244-0991-8/07IEEE2007
- L.L.Lai,Senior Member IEEE,T.Y.Nieh,D.Vujatovic,Y.N.Ma,Y.P.Lu,Y.W.Yang,H.Braun ,”Particle Swarm Optimization for Economic Dispatchof units with Non-smooth Input-Output Characteristic Functions,”1-59975-028-7/05 IEEE 2005
- Masashi Yoshimi,Swarup,K.S.YoshioIzui,” Optimal Economic Power Dispatch Using Genetic Algorithms,”pp 0-7803-1217-1 IEEE 1993
- A.A.EI-Keib, H.Ma,J.L.Hart,”Environmentally Constrained economic Dispatch Using the LaGrangianERelaxationMethod,IEEETransactiomonpower systems, vol.9, 1994
- k.Chandram*,N.subrahmanyam,”Brent method for Economic Load Dispatch with Transmission Losses,”IEEE ,2007.
- Masahiko Tanimoto*1,YoshioIzui*1 koichi Hirose*2 ,Shizuka Nakamura*2,” Advanced Economic Dispatching Control Algorithm usingDynamic unit Model and interior point method,”APSCOM-97,1997.
- Yun-He hou,Li-Juan Lu,Xin-Yin Xiong,Yao-wuwu,” Economic dispatch of power systems Based on the Modified Particle SwarmOptimization Algorithm,’IEEE,2005.
- Rania Hassan *BabakCohanim Olivier de week ,”A comparison of particle swarm optimization and the genetic algorithm,”IEEE,2005.
|