ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
B.R Sharma1, Hemanta Konwar2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The problem of mass distribution in an unsteady two dimensional flow of a viscous, incompressible, thermally and electrically conducting binary fluid mixture between two infinite vertical parallel plates under the influence of chemical reaction, uniform magnetic field and temperature gradient is studied. The magnetic field lines are assumed to be fixed relative to the moving plates. The governing partial differential equations are first transformed into ODEs by the method of separation of variables and then solved numerically by using MATLAB’s built in solver bvp4c. The solution for the concentration of the rarer and lighter component of the binary fluid mixture for different values of Reynolds number, chemical reaction parameter, Schmidt number, thermal diffusion number and Peclet number are presented graphically to analyse their effects on mass distribution of the components of the binary fluid mixture.
KEYWORDS |
| Binary fluid mixture, unsteady, MHD Couette flow, magnetic field, chemical reaction, mass distribution |
I. INTRODUCTION |
| MHD Couette flow between two parallel plates is a classical problem that has important applications in various industrial processing such as power generators and MHD pumps used in chemical energy technology, accelerators, aerodynamics heating, polymer technology, petroleum technology and also in many material processing applications. Heat and mass transfer problems with chemical reaction are of great importance in several processes. The effect of chemical reaction depends upon whether the reaction is homogeneous or heterogeneous. In well-mixed systems, the reaction is heterogeneous if it takes place in the interface and homogeneous if it takes place in solution. In most cases the reaction rates depends upon the concentration of species. A reaction is said to be of first order if the rate of reaction is directly proportional to the species concentration. When fluid moves through a magnetic field then an electric current may be induced and in turn current interacts with the magnetic field to produce a body force on fluid. The influence of a magnetic field in viscous incompressible flow of electrically conducting fluid is used in plastic technology to manufacturing of rayon, nylon etc. |
| In a binary fluid mixture the diffusion of individual species takes place by three mechanisms namely ordinary diffusion, baro-diffusion and thermo-diffusion. The diffusion flux i of rarer and lighter components is given by Landau and Lifshitz [1] as |
| where ρ is the density of the binary fluid mixture, kpD is the baro- diffusion coefficient, kTD is the thermo- diffusion coefficient and c is the concentration of rarer and lighter components of the binary fluid mixture. The ordinary diffusion to the mass flux is seen to depend in a complicated way on the concentration gradients of the components present in the mixture. If there is a pressure gradient imposed on the system then baro-diffusion shows that there may be a net movement of the components in the mixture. Thermal diffusion indicates the tendency for species to diffuse under the influence of a temperature gradient. It was shown by Groot and Mazur [2] that if separation due to thermal diffusion occurs then it might even render an unstable system to stable one. This effect is quite small, but devices can be arranged to produce very steep temperature gradients so that separation of mixtures are affected. Bodosa et al. [3] analysed the heat transfer between two horizontal plates in presence of a uniform magnetic field. Sharma and Singh [4, 5] studied analytically the Soret effect on de-mixing of species in hydro-magnetic flow of a binary mixture of incompressible viscous fluid between two parallel plates, first taking the plates horizontal and second by taking the plates vertical. Attia. H. A. [6] studied the effect of variable properties on the unsteady Couette flow with heat transfer considering the Hall Effect. Sharma et al. [7, 8, 9] investigated analytically the effect of magnetic field on separation of binary fluid mixture for different geometries. Das and Jana [10] investigated heat and mass transfer effects on unsteady MHD free convective flow near a moving vertical plate in porous medium. Sharma et al. [11, 12, 13] studied the effects of axial and radial magnetic field on de-mixing of a binary fluid mixture. Sharma, Singh and Gogoi [14] discussed the effects of magnetic field and temperature gradient on separation of a binary fluid mixture in unsteady Couette flow analytically. They did not consider the effect of chemical reaction in their investigations. |
| The aim of this research paper is to investigate numerically the effect of chemical reaction on mass distribution in unsteady, incompressible, viscous, electrically conducting binary fluid mixture between two infinite vertical parallel plates both of which are moving with equal velocities in opposite directions. |
II. MATHEMATICAL MODELLING |
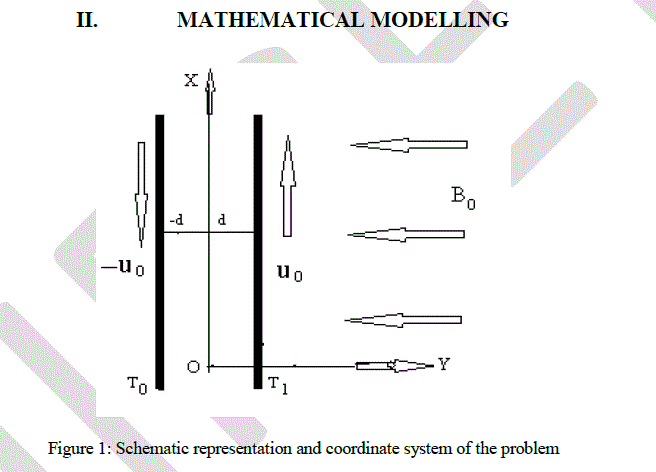 |
| The unsteady MHD flow of an incompressible viscous electrically conducting fluid between two infinite vertical parallel plates at a distance 2d apart is considered under the influence of a uniform transverse magnetic field. The flow is assumed to be along the X-direction, which is in the vertical direction through the central line of the channel and Y-axis is along the horizontal direction [see Fig 1]. The plates of the channel are at y = ± d and that the relative velocity between the two plates is 2u0. A uniform magnetic field of strength B0 is applied perpendicular to the plates. The plate y = - d is maintained at temperature T0, while the temperature of the plate at y = d varies exponentially with time having initial temperature T1 (T1 >T0). Since the plates are considered infinite in X- direction, hence all the physical quantities will be independent of x. Therefore all the physical variables become functions of y and t only. |
| We make the following assumptions: |
| ïÃâ÷ The magnetic field is weak. The magnetic field lines are assumed to be fixed relative to the moving plates. |
| ïÃâ÷ Boussinesq approximation is applied. |
| ïÃâ÷ Plates are non-conducting. |
| ïÃâ÷ No pressure gradient in the flow field. |
| ïÃâ÷ No applied voltage and hence electric field is absent. |
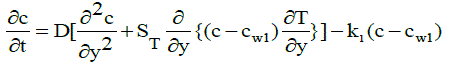 |
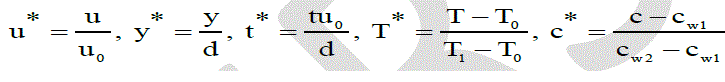 |
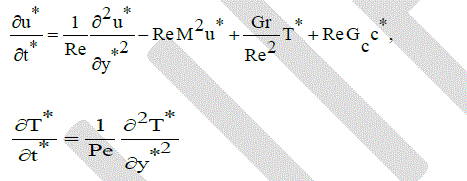 |
| are Reynolds number, Hartmann number, Grashof number, Chemical reaction parameter, Schmidt number, Mass Grashof number, Prandtle number, Peclet number and thermal diffusion number respectively. |
III. SOLUTION OF THE PROBLEM |
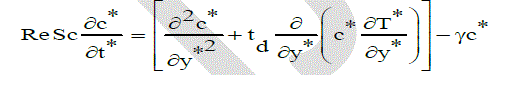 |
IV. RESULTS AND DISCUSSIONS |
| Numerical calculations have been carried out for concentration of the rarer and lighter component of the binary fluid mixture for various values of the parameters Re, Pe, Sc, γ and td |
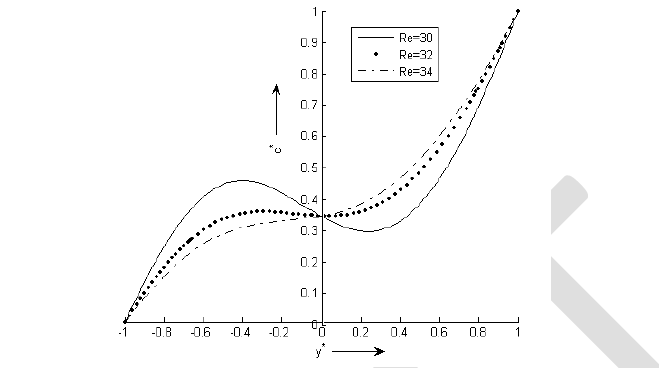 |
| Figures 2 reveals that increase in the value of Reynolds number (Re) decreases the concentration of the rarer and lighter component of the binary fluid mixture at any point in the region [-1, 0] and increases the concentration of the rarer and lighter component of the binary fluid mixture at any point in the region [0, 1]. Thus the concentration of the rarer and lighter component of the binary fluid mixture can be increased by increasing the value of the Reynolds number (Re) i.e. with the increase in the value of density of the mixture, with the increase in the values of the magnitude of velocity of the plates, with the increase in the values of the distances between the plates, and with the decrease in the viscosity of the fluid mixture. |
 |
| Figure 3 signifies that if the value of the chemical reaction parameter γ increases then there is a little increase in the concentration of the rarer and lighter component of the binary fluid mixture in the region -1≤y* ≤ - 0.344 and then decreases in the region -0.344≤y* ≤1. Thus by decreasing the value of chemical reaction parameter γ the concentration of the rarer and lighter component in the binary fluid mixture can be increased. |
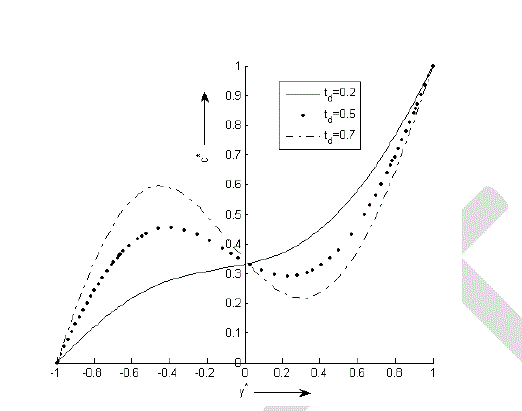 |
| Figure 4 depicts that as the value of the thermal diffusion parameter td increases the concentration of the rarer and lighter component of the binary fluid mixture increases sharply at any point in the region y * ≤ 0 and there is a sharp decrease in the concentration of the rarer and lighter component of the binary fluid mixture at any point in the other half of the channel. Thus by increasing in the value of thermal diffusion parameter td which depends on Soret number and temperature gradient between the two plates can increase the concentration of the rarer and lighter component of the binary fluid mixture at any point in the region [-1, 0] and can decrease the concentration of the rarer and lighter component of the binary fluid mixture in the region [0, 1]. |
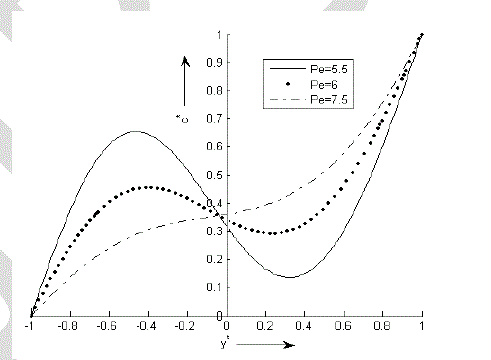 |
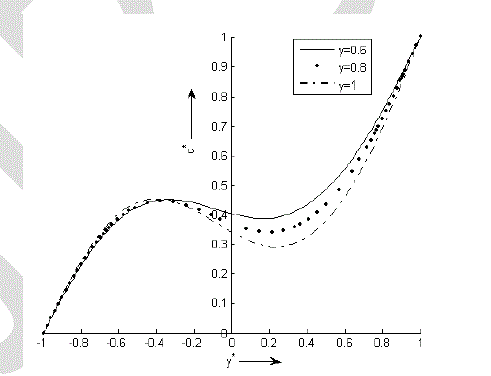
| Figure 5 indicates that if the value of Peclet number (Pe) increases then concentration of the rarer and lighter component of the binary fluid mixture decreases at any point in the region [-1, -0.0505] while reverse effect is observed at any point in the region [-0.0505, 1]. Concentration of the rarer and lighter component of the binary fluid mixture can be increased by increasing the value of Pe. |
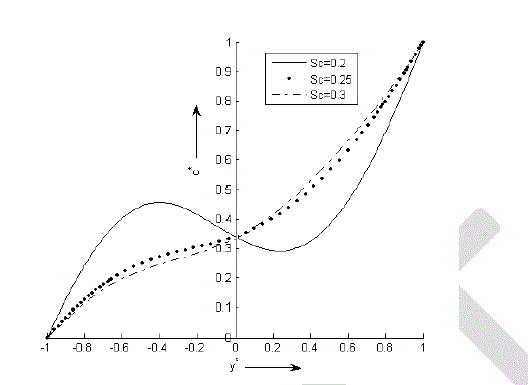 ` ` |
| From the Figure 6 it is clear that the concentration of the rarer and lighter component of the binary fluid mixture decreases gradually in the region y* ≤ 0 and then increases in the other half of the channel as the value of Schmidt number (Sc) increases. Thus by increasing the value of Schmidt number (Sc) which depends on kinematic viscosity and mass diffusion can decrease the concentration of the rarer and lighter component of the binary fluid mixture at any point in the region [-1, 0] and can increase the concentration of the rarer and lighter component of the binary fluid mixture at any point in the region [0, 1]. |
V. CONCLUSION |
| From the observations it is clear that the non dimensionless parameters Re, γ, td, Sc and Pe play important roles in the mass distribution of species of a binary fluid mixture in an unsteady Couette flow between two vertical moving plates. Concentration of the rarer and lighter components of the binary fluid mixture increases as y* increases from -1 to 1 with the increase in the values of Re, Pe and Sc and concentration of the rarer and lighter component of the binary fluid mixture decreases with the increase in the value of td and chemical reaction parameter γ. Thus Re, Pe, Sc enhance the rate of separation and td, γ diminish the rate of separation of the rarer and lighter component of the binary fluid mixture. |
ACKNOLEDGEMENTS |
| The second author is thankful to Nagaland Government for providing financial support and to Dibrugarh University for providing all academic facilities during the preparation of this research paper. |
References |
|