Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Effect of SRS-XPM-FWM-ASE Nonlinearity in Optical Communication System

Yogita Thareja1 , Gurmeet Singh2
  1. M-Tech Scholar, Dept. of ETE, PDM College of Engineering, Bahadurgarh, Haryana, India
  2. Assistant Professor, Dept. of ETE, PDM college of Engineering, Bahadurgarh, Haryana, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In all-optical communication system, the signal remains in optical domain between the transmitter and receiver. As the optical signal propagates from the transmitter towards receiver, due to physical layer impairments of the network, its quality degrades. The factors affecting the physical layer of the optical network are the linear and nonlinear effects of fiber. In this paper analysis the linear and non-linear effects present in optical communication system. The performance of the optical communication system due to collective effect of FWM and SRS and due to combined effect of FWM and XPM has been discussed. Limitations of amplifier and its optimal location have also been discussed. In this paper the performance evaluation based on Q-factor vs transmitted power for FWM-XPM, SRSFWM, SRS-XPM and SRS-XPM-FWM-ASE nonlinearity in optical communication for 8 channels and 16 channels communication system.

Keywords
Stimulated Raman scattering (SRS), Amplified spontaneous emission noise (ASE), Cross phase modulation (XPM), Self phase modulation (SPM), Four wave Mixing (FWM).

INTRODUCTION
The need for large bandwidth in the transport network fabric has led to the acceptance of optical network as the technology of choice for the core transport function. Optical fiber, as a medium in optical network, provides over 40 THz of available bandwidth that can be efficiently utilized using wavelength division multiplexing (WDM) [1, 2]. In WDM, the entire optical bandwidth is divided into a number of channels centred at different wavelengths [3]. The WDM network operates as an optical transport network carrying the traffic from existing network technologies (e.g., SONET/SDH, ATM, IP) and transporting them using light paths. 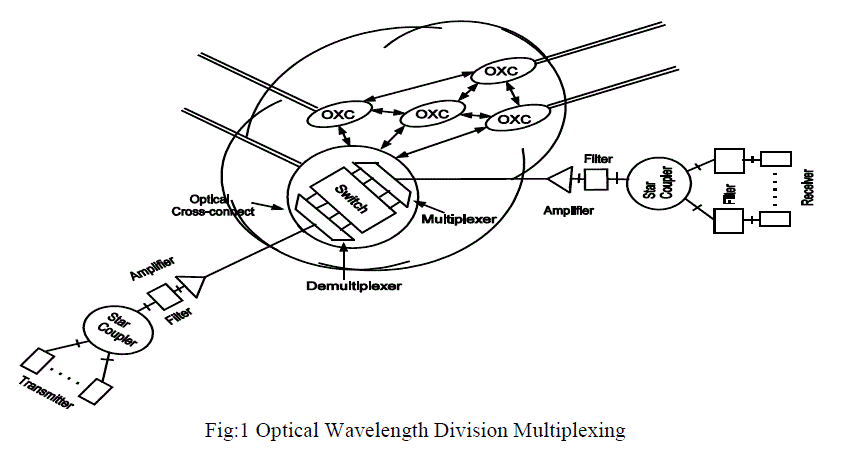Thus the WDM infrastructure consists of access networks connected through WDM rings with the help of optical cross-connects (OXC) to the WDM mesh network [4, 5]. A typical configuration of all optical wavelength division multiplexing network is shown in Fig. 1. The impact of non-linear impairments on quality of transmission (QoT) is strongly dependent on the accumulated power and on the individual power of the other optical channels transported in parallel on the same fiber whereas the impact of linear impairments is independent of the power of each of the optical channels transported on the same fiber. In case of linear impairments, QoT can be evaluated individually for the different optical channels sharing the same fiber.
When nonlinear impairments are considered, QoT of each optical channel transported on the fiber depends on the number and the power of other channels transported simultaneously on the same fiber. The non-linear impairments are self-phase modulation (SPM), cross phase modulation (XPM), four wave mixing (FWM), stimulated Brillouin scattering (SBS) and stimulated Raman scattering (SRS) while the linear impairments are amplified spontaneous emission (ASE) noise generated by EDFAs, polarization mode dispersion (PMD), chromatic dispersion (CD) of fiber and OXC crosstalk. Due to non-linear and linear impairments, quality of the signal at some intermediate node may degrade beyond recognition. In such cases, regenerators have to be placed at intermediate nodes.
The paper is organized as follows. In sections II, non-linear impairments of optical network are discussed. . In sections III, linear impairments of optical network are discussed. In section IV, simulation results for the performance evaluation based on Q-factor vs transmitted power for FWM-XPM, SRS-FWM, SRS-XPM and SRS-XPM-FWM-ASE nonlinearity in optical communication for 8 channels and 16 channels communication system are discussed. We conclude the article in Section V and discuss several outstanding research issues.

NON-LINEAR IMPAIRMENTS
These impairments are due to non-linear effects in the optical fiber and can arise either due to change in the refractive index of the medium with optical intensity (power) or due to inelastic-scattering phenomenon. The non-linear effects are briefly explained below.

A. SELF PHASE MODULATION (SPM)
SPM occurs due to the non-linear phase modulation of an optical pulse caused by its own intensity in an optical medium. As an optical pulse travels down the fiber, the leading edge of the pulse causes the refractive index of the fiber to increase causing a blue shift while the falling edge of the pulse decreases the refractive index causing a red shift. These shifts introduce a frequency chirp on each edge and the signal is broadened in the frequency domain by an amount given as
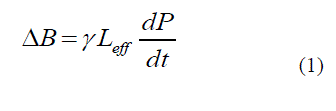image
where dp/dt is the time derivative of the pulse power, γ is the non-linear coefficient and L eff is the effective length. The primary effect of SPM is to broaden the pulse in the frequency domain, keeping the temporal shape unaltered, while dispersion causes broadening of the pulse in time domain keeping the spectral contents unaltered. Hence, broadening of the pulse occurs only when the shifts introduced by the frequency chirp interact with fiber dispersion. The effects produced by SPM and dispersion are opposite in nature and by choosing proper pulse shape and input power, one effect will compensate for another, leading to undistorted pulse in both time and frequency domains. SPM is the strongest among the Kerr effects for DWDM systems working at 100 GHz spacing and the chirp depends on the input pulse shape.

CROSS PHASE MODULATION (XPM)
XPM originates from the intensity dependence of the refractive index, which results in intensity dependent phase-shift as signal propagates through the fiber. When there is more than one optical signal propagating through the fiber as in multichannel WDM, the non-linear phase shift of a signal not only depends upon its own power but also on the power of other signals [23]. For example, if there are four signals, the non-linear phase shift of the first signal [22] is given by where Pi i =1 to 4 are the powers of the four signals and Leff the effective length of the fiber. The first term in above equation is due to SPM while other terms are due to XPM that represents the phase-modulation (PM) process. In presence of group velocity dispersion (GVD), this PM is converted into IM (intensity modulation), which degrades the quality of the signal. The XPM-induced phase shift can occur only when two pulses overlap in time due to which the intensity-dependent phase shift and consequent chirping is enhanced, leading to asymmetric spectral broadening and distortion of the pulse shape.
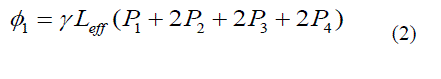image
where Pi i =1 to 4 are the powers of the four signals and Leff the effective length of the fiber. The first term in above equation is due to SPM while other terms are due to XPM that represents the phase-modulation (PM) process. In presence of group velocity dispersion (GVD), this PM is converted into IM (intensity modulation), which degrades the quality of the signal. The XPM-induced phase shift can occur only when two pulses overlap in time due to which the intensity-dependent phase shift and consequent chirping is enhanced, leading to asymmetric spectral broadening and distortion of the pulse shape.

FOUR WAVE MIXING (FWM)
In a WDM system, due to the non-linear nature of the refractive index, when signals of frequencies fi, fj, fk propagate in the fiber, non-linear interaction will generate new components [23] at frequencies (fi ± fj ± fk) . Thus,
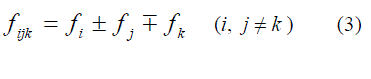image
For example, if i=1, j=2 and k=3, FWM components that are generated (excluding the case i=k and j=k) are f 321f 231 , f 312 , f 213 , f 332 , f 331 , f 223 , f 221 , f 113 and f 112 . Some of these generated FWM components lie on the transmitted carrier causing interference [24]. The generated signal power is expressed as
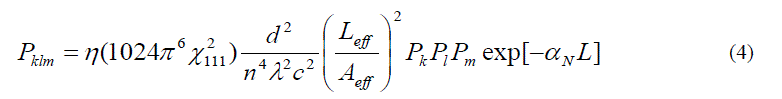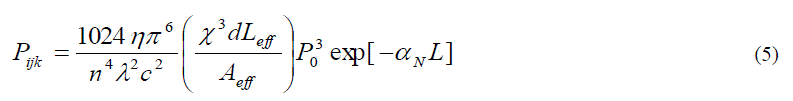image
image
image
The total FWM power generated at frequency f x is given by [37]
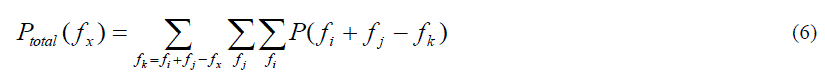image
The crosstalk due to FWM is the dominant non-linear effect in long-haul DSF based WDM systems. If the channels are equally spaced (known as equally spaced channel allocation scheme (ESCA)) the number of FWM components generated grows rapidly as the number of channels is increased.

STIMULATED RAMAN SCATTERING (SRS)
SRS is due to interaction of incident light wave with vibrational modes of silica molecule i.e., if two or more optical signals at different wavelengths are injected into a fiber, SRS causes energy from lower wavelength channels to be transferred to the higher wavelength channels. This in turn reduces the signal-to-noise ratio of the lower wavelength channels and introduces crosstalk on higher wavelength channels which can lower the information carrying capacity of the system. The threshold power in case of SRS can be estimated as [22]
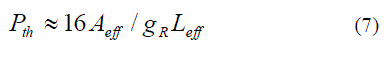image
where gR is the Raman gain and Leff the effective length of the fiber. If the fiber is sufficiently long, then Leff ≈ 1/α. In that case
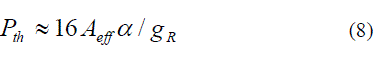image
The value of gR is 1 x 10-13 m/W for silica at λ =1550 nm. The value of α as 0.2 dB/km and Aeff as 55 2 μm, results in Pth equal to 570 mW. Hence, the effect of SRS is insignificant in case of single channel.

LINEAR IMPAIRMENTS

A. CHROMATIC DISPERSION (CD)
A light source generates signal with closely spaced wavelengths. As the refractive index of fiber is a function of wavelengths, these wavelengths travel through the fiber at different speed. It gives rise to pulse broadening at the receiver which results in inter symbol interference (ISI). CD is a measure of change of refractive index with wavelength and is expressed as ps/nm.km.

B. AMPLIFIED SPONTANEOUS EMISSION (ASE) NOISE
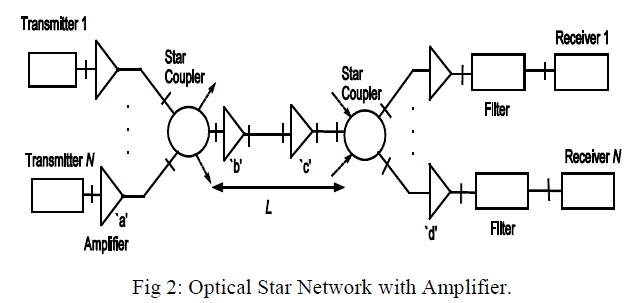
Optical amplifiers play an important role in the design of long haul optical communication networks. EDFA is the commonly used optical amplifier in a long-haul WDM network. It has the capability of amplifying multiple wavelengths simultaneously. The amplifier can either be placed at position ‘a’ (as booster amplifier), or at position ‘b’ and ‘c’ (as in-line amplifier), or at position‘d’ (as pre-amplifier) as shown in Fig. 3.
image
Amplifier produces amplified spontaneous emission (ASE) noise. The average total power of amplified spontaneous emission (PASE) is given by
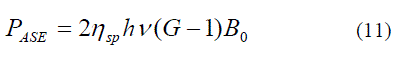image
where hv is the photon energy, G the amplifier gain, B0 the optical bandwidth of the fiber. In the above equation, the parameter nsp represents the population inversion factor and is equal to N2/(N2 –N1) where N2 and N1 are population at the excited levels and lower level respectively. The typical value of nsp ranges from 1.4 to 4. While designing optical WDM networks, it becomes important to find the optimal locations of optical amplifiers as it not only increases the cost of network, but also results in accumulation of ASE noise resulting in a reduction in the SNR/degradation in performance.

RESULT AND DISCUSSION
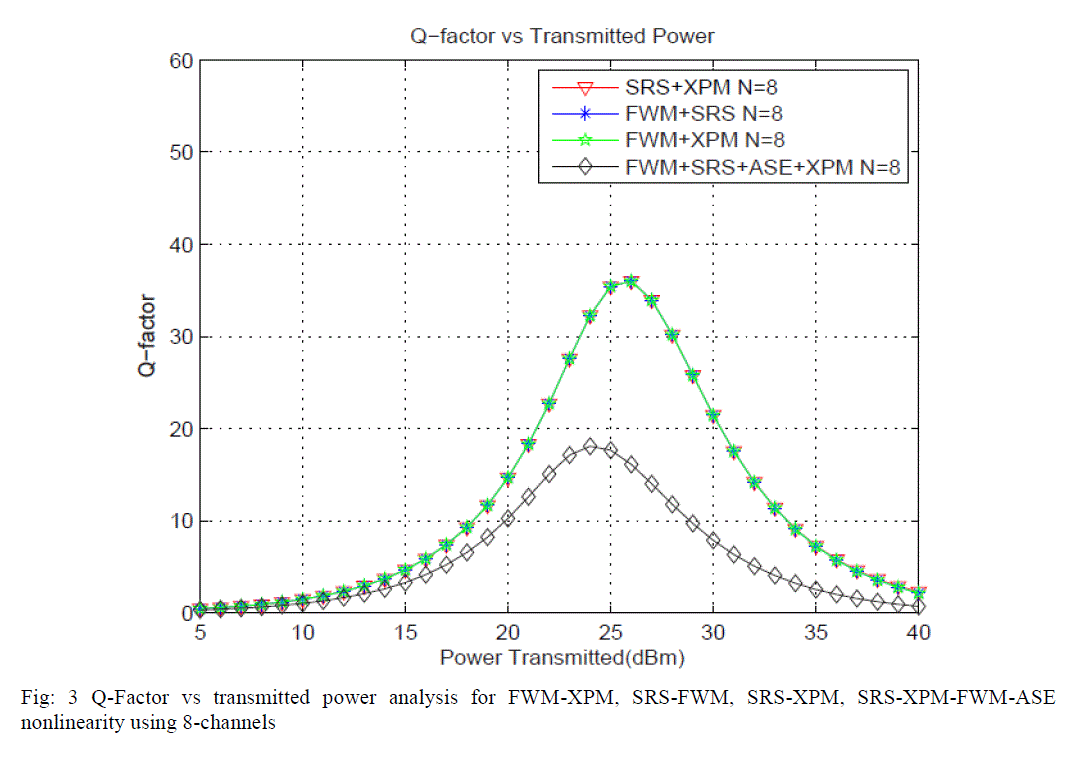
Simulation result analysis the linear and non-linear effects present in optical fiber emphasizing those that result in degradation of performance in optical communication system. The performance of the optical communication due to collective effect of FWM and SRS and due to combined effect of FWM and XPM has been discussed. Result shows that the analysis based on Q-factor vs transmitted power due to combined effect of FWM-XPM, SRS-FWM, SRSXPM, SRS-XPM-FWM-ASE nonlinearity, in optical communication for 8 channels and 16 channels communication system. . 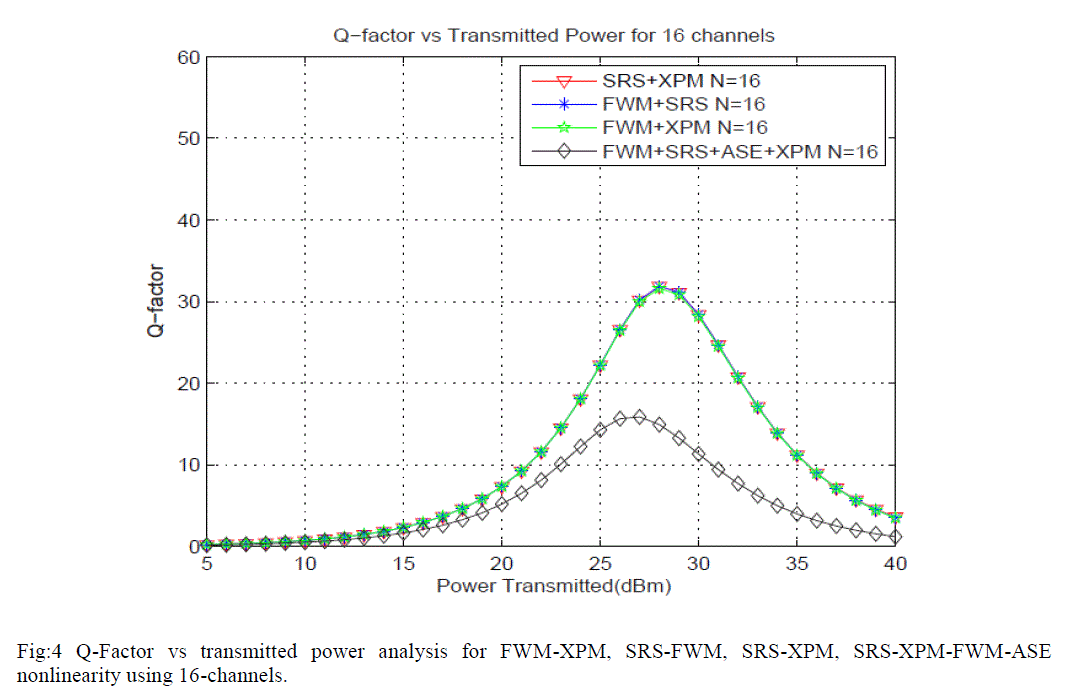Result also shows that the analysis of Q-factor due to combined effect of FWM-XPM, SRS-FWM, SRSXPM, SRS-XPM-FWM-ASE nonlinearity, in optical communication for 8 channels and 16 channels communication system. Fig: 3 shows the Q-Factor vs transmitted power analysis for FWM-XPM, SRS-FWM, SRS-XPM, SRS-XPMFWM- ASE nonlinearity using 8-channels. Fig: 4 shows the Q-Factor vs transmitted power analysis for FWM-XPM, SRS-FWM, SRS-XPM, SRS-XPM-FWM-ASE nonlinearity using 16-channels.
image
image

CONCLUSION
In this paper, non-linear and linear impairments present in fiber that degrade the performance of optical communication system have been reviewed. As the noise generated by optical amplifier degrades the performance of optical communication system, placement of amplifier is an important issue in designing all-optical optical communication system. In this paper result show that the combine effect of the FWM-XPM, SRS-FWM, SRS-XPM, SRS-XPM-FWMASE nonlinearity based on Q-factor with different number of channels.

References