International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

EFFECTS OF MACHINE PARAMETERS ON PERFORMANCE OF SELF-EXCITED INDUCTION GENERATOR UNDER UNBALANCED OPERATION

Yatender Chaturvedi1 , Kanwarjit Singh Sandhu2
  1. Research Scholar, Dept. of Electrical Engineering, National Institute of Technology, Kurukshetra, India
  2. Professor, Dept. of Electrical Engineering, National Institute of Technology, Kurukshetra, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The unbalanced loading on SEIG is the common phenomenon which generally occurs due to singlephase load(domestic load) and may deteriorate the performance of such machines. This paper presents a new model which has been used to analyze the effects of machine leakage reactance on performance analysis of SEIGs under the unbalanced operations. From simulation results it is found that degree of unbalance is strongly affected by the machine parameters as compared to its resistances. The simulation study as performed on 15kw machine may be useful to design the machine for such operations.

Keywords
Self-excited induction generator (SEIG), unbalanced operation , degree of unbalance, wind energy.

NOMENCLATURE
a e j(2 π / 3)
F per-unit frequency
ν per-unit speed
Ca, Cb, Cc shunt excitation capacitances of respective phases
Ral, Rbl, Rcl load Resistance of respective phases
Xal,Xbl,Xcl load reactance of respective phases
R1 ,R2 stator and rotor resistance per phase
X1 ,X2 stator and rotor leakage reactance per phase
Vgp , Vgn per phase air gap voltages of positive and negative sequence networks
Vp , Vn per phase positive and negative sequence voltages
Ip, In per phase stator currents of positive and negative sequence networks
YP, Yn per phase equivalent admittance seen from open load terminals of positive and negative sequence networks respectively.
Zlp, Zln per phase positive and negative sequence load impedance
Xmp, Xmn per phase magnetizing reactance of positive and negative sequence networks
K Degree of unbalance ( vn/vp)

INTRODUCTION
The self-excited induction generator (SEIG) seems to be suitable for the conversion of wind energy in to the electrical energy for remote & windy locations. These machines may be used to fulfil the local demands of these areas. Selfexcited induction generator has many advantages such as brushless rotor construction, absence of separate d.c source, easy to maintenance, reduced size etc. Such generators are being given more attention since last two decades for standalone application.
Self-excitation phenomenon in an induction generator occurs when its rotor is driven by a prime mover and an appropriate capacitor bank is connected across the stator terminals. The performance analysis of three-phase selfexcited induction generator under balanced operation needs the proper electrical circuit representation and the appropriate mathematical modeling. The conventional equivalent circuit of an SEIG has been used [1] for performance evaluation which is based on the loop impedance method. [2] adopted the nodal admittance approach for analyzing the performance of SEIG. [3] shows the importance of excitation requirements where as [4] discussed their limits for successful operation. In order to reduce the computational efforts, an iterative technique has been proposed in [5]. [6] Proposed a new equivalent model that includes the active power source which also makes the analysis simple. However, the analysis of such generators under unbalanced operations has been given considerable less attention. The unbalanced mode of operations of SEIG generally arises due to single-phase loading (domestic load) or due to use as distributed generator where balanced operation is difficult to achieve. Very few literatures has been reported for the performance evaluation of such generators under unbalanced conditions. In contrast to balanced operation [7] proposed a simplified circuit for the analysis of SEIG under unbalanced mode of operations. A new model for various generatorload combinations was proposed by [8]. [9] carried out the study of SEIG for unbalanced conditions using line current injection method. [10] derived the new mathematical expressions using symmetrical component approach where as [11] continues the same using two port model for unbalanced operations of SEIG. A study of unbalanced operation of SEIG was given by [12] in which core losses was also taken in to consideration. [13] continues the study of unbalanced operation and proposed a new model based upon load decoupling across the machine terminals and incorporates the shunt magnetizing branch in the negative sequence network. This paper presents a new model that has been used to analyze the effects of machine parameters on performance estimation of SEIG under unbalanced load and excitation as well.

MODELLING
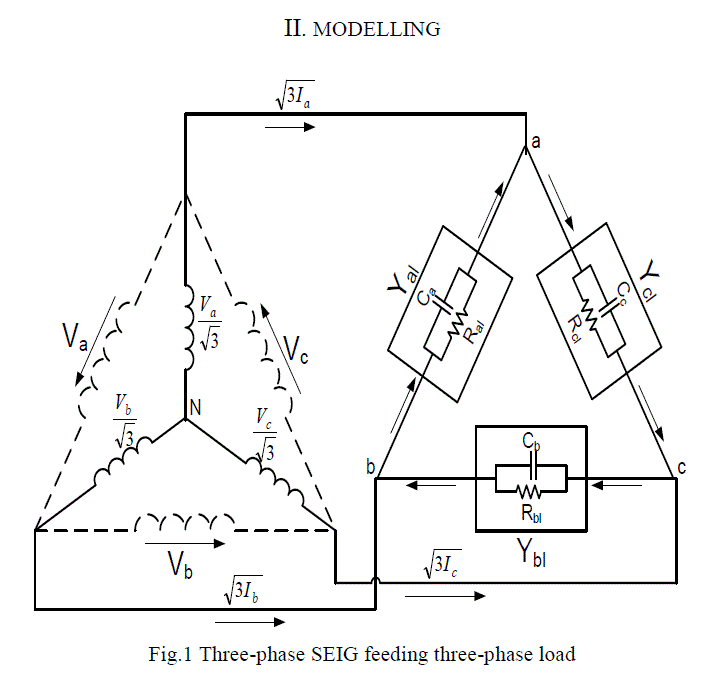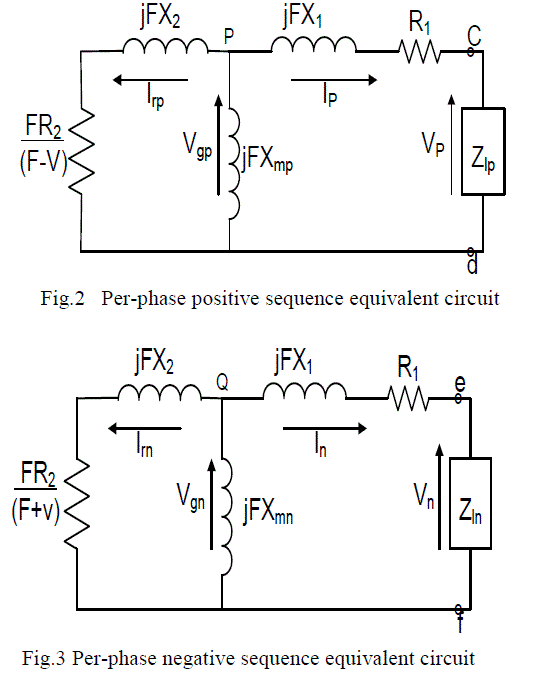
image
Fig.1 represents the three phase self-excited induction generator feeding a three phase unbalanced load, where as Fig.2 & Fig.3 represents the per-phase positive & negative sequence equivalents circuits.
image
By applying Kirchhoff‟s current law at nodes a,b,c of Fig.1, the nodal admittance matrix may be formed as:
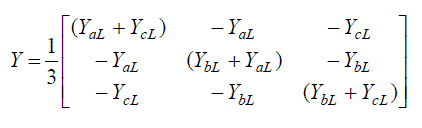image (1)
Where, Yal, Ybl, Ycl are the phase admittance which can be yields from the addition of admittances offered by the load & excitation capacitance of the respective phases. From the symmetrical component theory
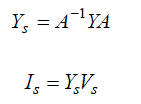image (2) &(3)
Where;
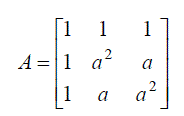image
Then from equation (2)
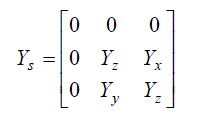image (4)
Where Yx, Yy and Yz may be obtained from the following matrix:-
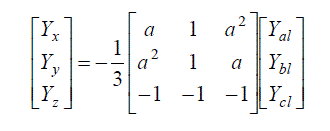image (5)
From equations (3) & (4);
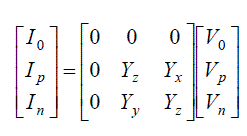image (6)
For a delta connected system, the sequence component of currents form equation (6) may be obtained as:
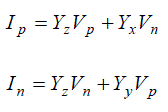image (7a) & (7b)
Now from the per-phase positive and negative sequence equivalent circuits of SEIG as shown in Fig.2 & Fig.3, following matrix in terms of positive and negative sequence component of currents may be obtained as:
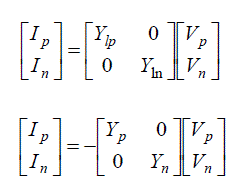image(8a) & (8b)
Few mathematical calculations from equations (7) & (8) results in to the following expressions of degree of unbalance and the load impedance of positive and negative sequence networks as :
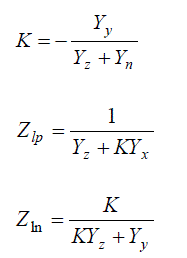image (9),(10),(11)

SOLUTION FOR GENERATED FREQUENCY AND MAGNETIZING REACTANCES
The generated frequency and magnetizing reactance off SEIG gets changes in any change in load, excitation and operating speed etc. These parameters are unknown and functioned in the equations formed by application of Kirchhoff‟s current law at nodes P & Q of the per-phase positive and negative sequence circuits of SEIG respectively. These equations are given as:
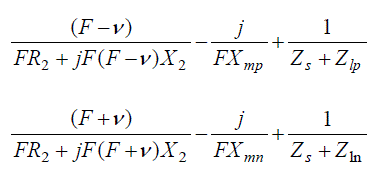image (12), (13)
Where;
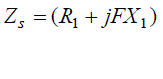image
The equations (12-13) may be solved for unknown parameters i.e. generated frequency & magnetizing reactance of positive and negative sequence networks using any optimization technique that gives the feasible solution for the unknown parameters.

PERFORMANCE EQUATIONS
After obtaining the unknown parameters i.e. generated frequency & magnetizing reactance of positive and negative sequence networks, the air gap voltage Vgp for positive sequence network may be obtained from the saturation curve of machine as in Appendix-I.
The positive & negative sequence components of voltages & currents may be obtained as:
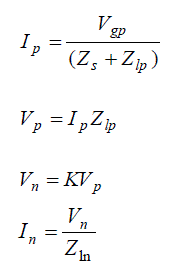image
From equations (14-17), The phase voltages & currents may be obtained as:
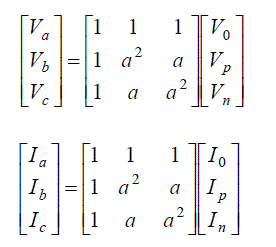image
Further the load currents in respective phases can be computed from the following matrix;
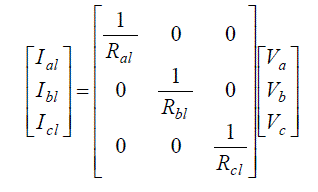image
Power output from the SEIG would be:
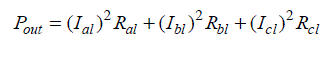image

RESULTS & DISCUSSION
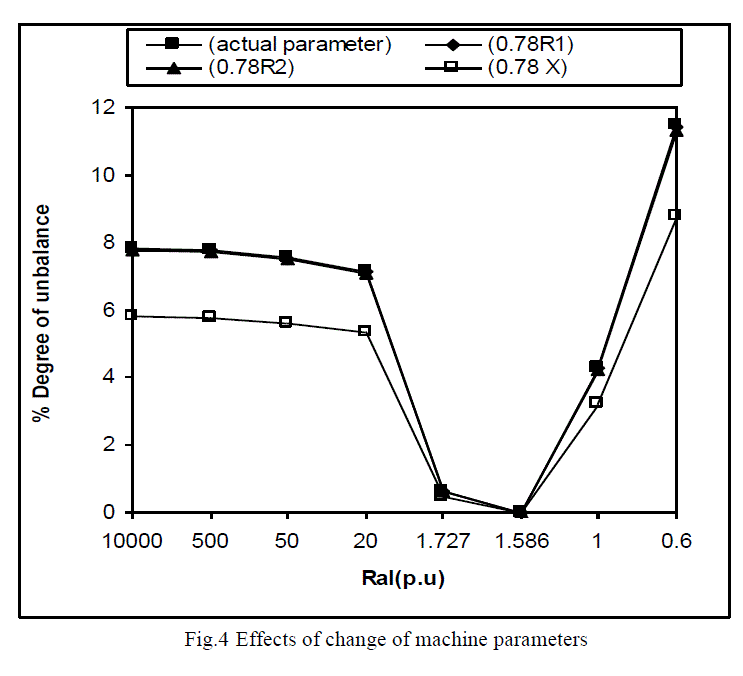
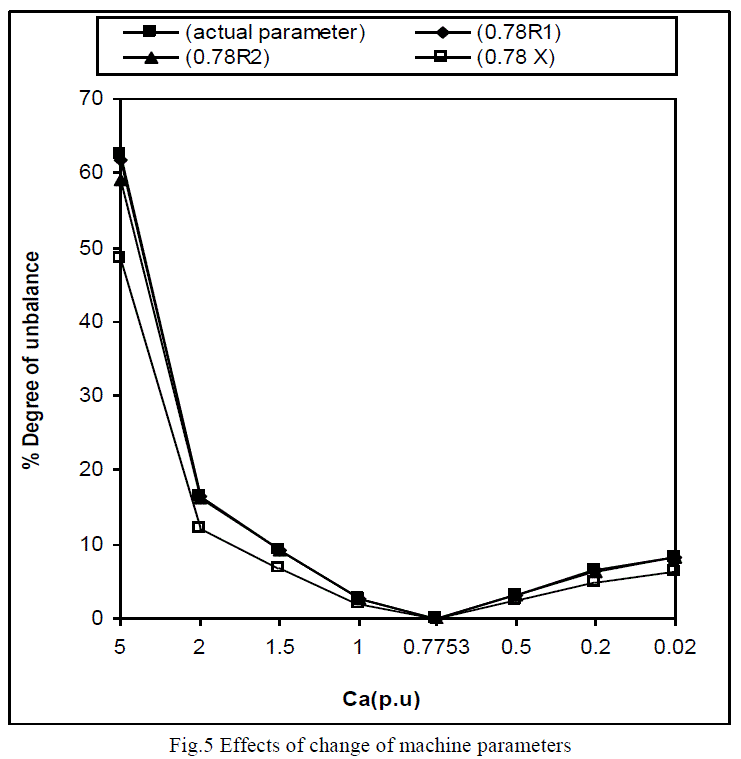
Proposed modeling of SEIG as explained in the previous section is used here to estimate the steady state performance of machine [Appendix1] under unbalanced operating conditions. From figure4 and figure5 it has been observed that there is a very little effect of resistances of stator and rotor on the degree of unbalance while it is strongly affected by the stator and rotor reactance (X1=X2=X). Therefore, focus of this study is to investigate the performance of SEIG due to „change in leakage reactance‟, under unbalanced operations.
image
image
(A) Effects due to unbalanced loading
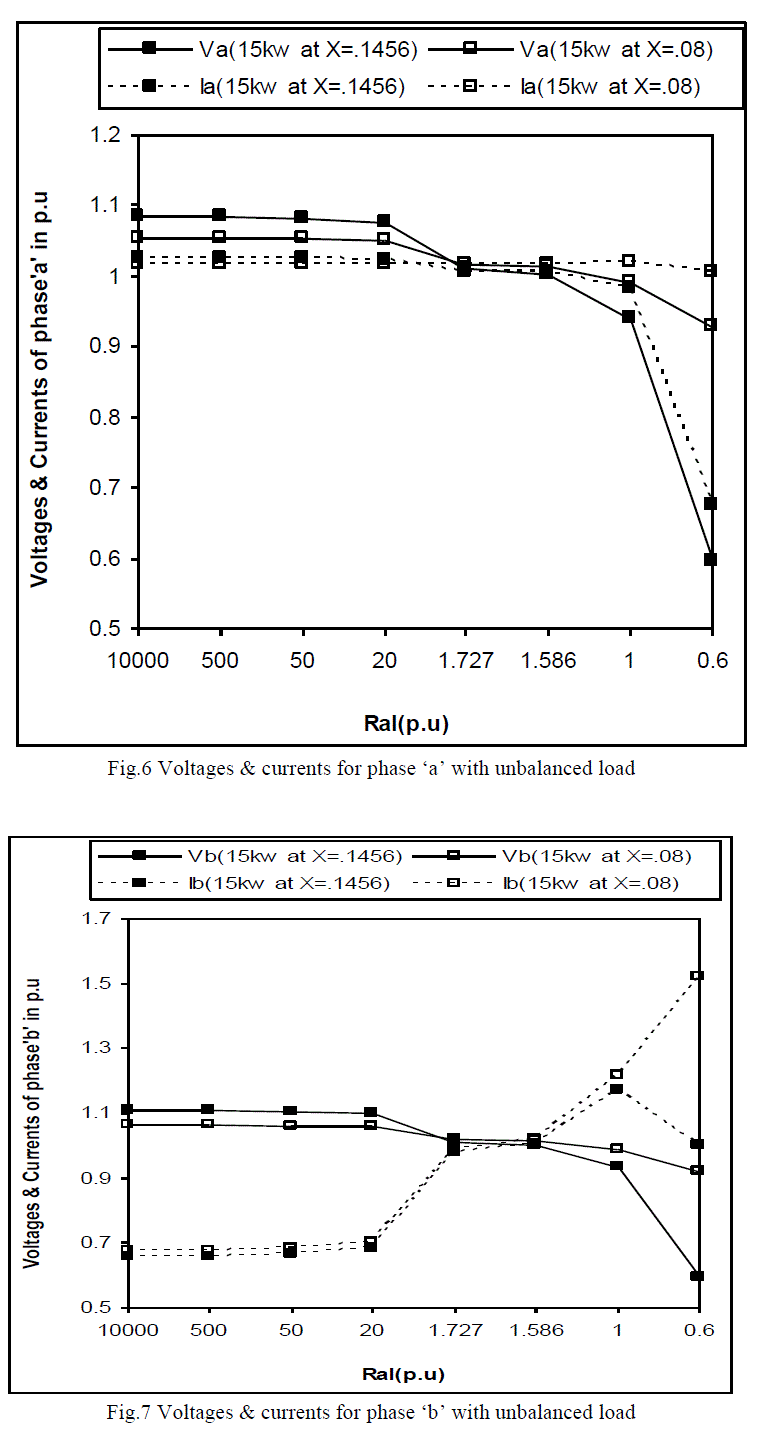
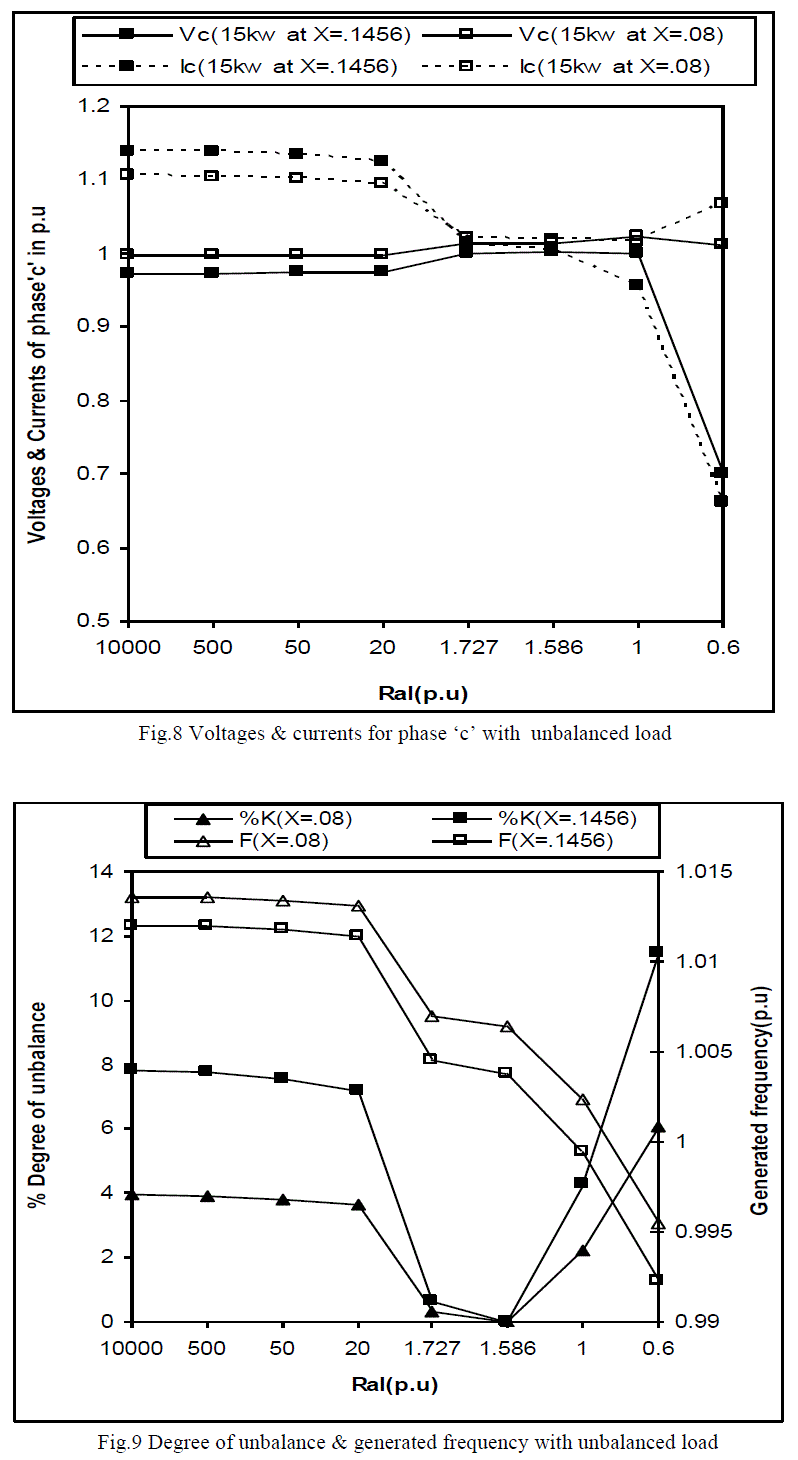
Fig.6 to Fig.9, shows the simulated results for voltages and currents of respective phases, degree of unbalance & generated frequency with different values of leakage reactance at a speed of 1.0288p.u when the unbalanced is achieved by varying the load resistance of one phase i.e. Ral. Large and small values of load resistance are corresponding to open and short circuit of that phase respectively. From Fig.6 to Fig.8 following observations was made:
• Open circuit of phase‟a‟ at actual stator & rotor reactance (X1=X2=0.1456p.u) leads the over voltage of any phase which may be limited to nominal operating limits by reducing stator and rotor reactance (X1=X2=0.08p.u)
• When approaching towards short circuit, generator tends to fail after excessive loading. However same machine with reduced value leakage reactance is capable to feed the load for short durations.
From Fig.9 it has been observed that with a low value of stator and rotor reactance results in to lower degree of unbalance and secondly it also improves the generated frequency.
image
image

(B) Effects due to unbalanced Excitation
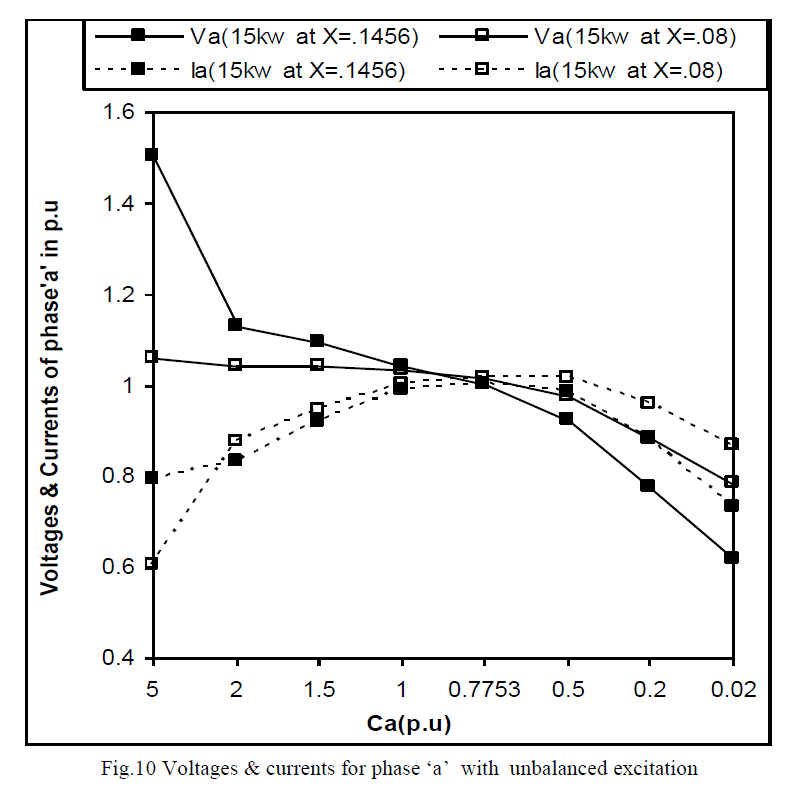
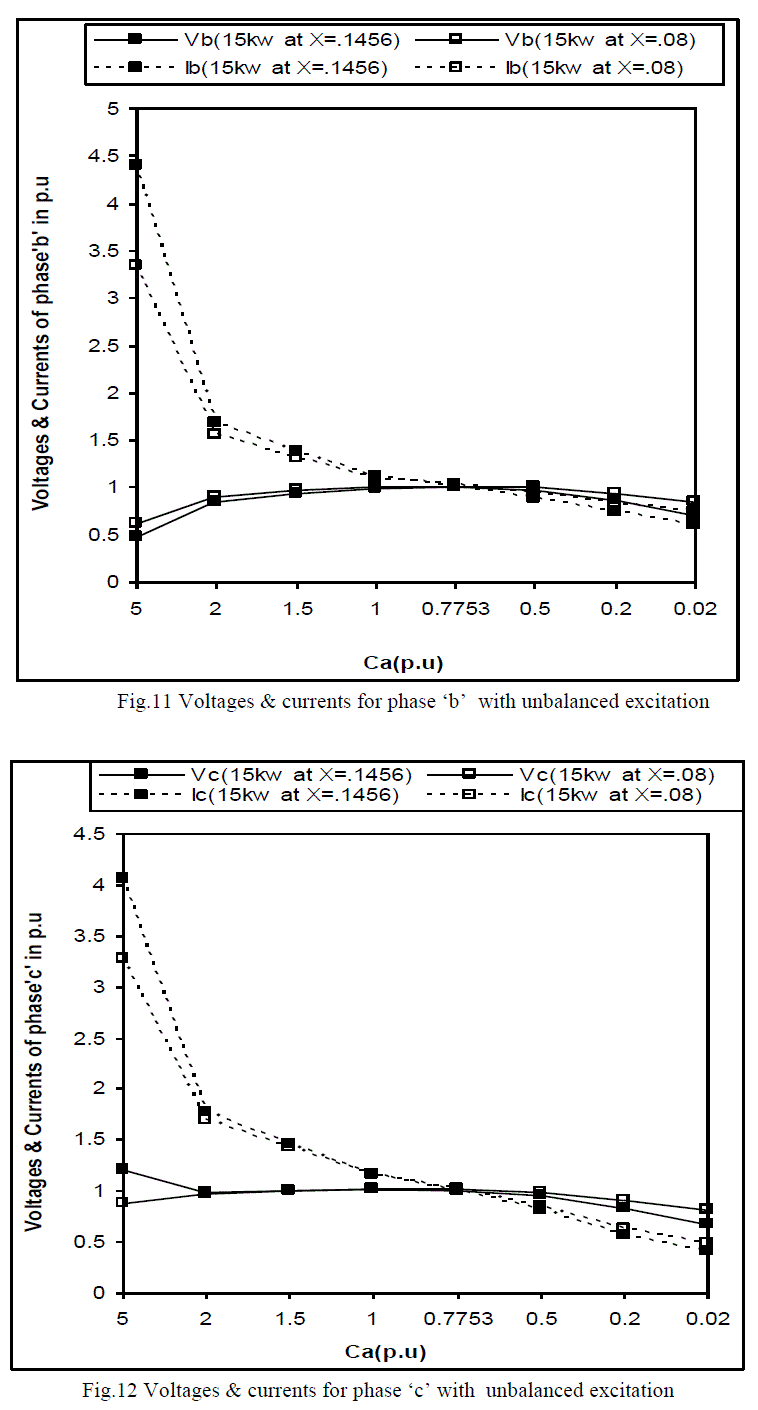
Fig.10 to Fig.13 shows the simulated results for voltages and currents of respective phases, degree of unbalance & generated frequency for actual and reduced stator and rotor reactance when the unbalanced is achieved by changing the capacitance of phase‟a‟. Large and small values of Ca are corresponding to short and open circuit operation respectively . Fig.10 to Fig.12 following observations was made:
• Change in excitation capacitor of phase‟a‟ results in to excessive over voltages & currents in some phases of the machine. This over voltages & over currents are several times as compared to the same change in the load resistance which is highly undesirable.
• The reduction of stator and rotor reactance, the undesirable over voltages & over currents may be limited to some extent.
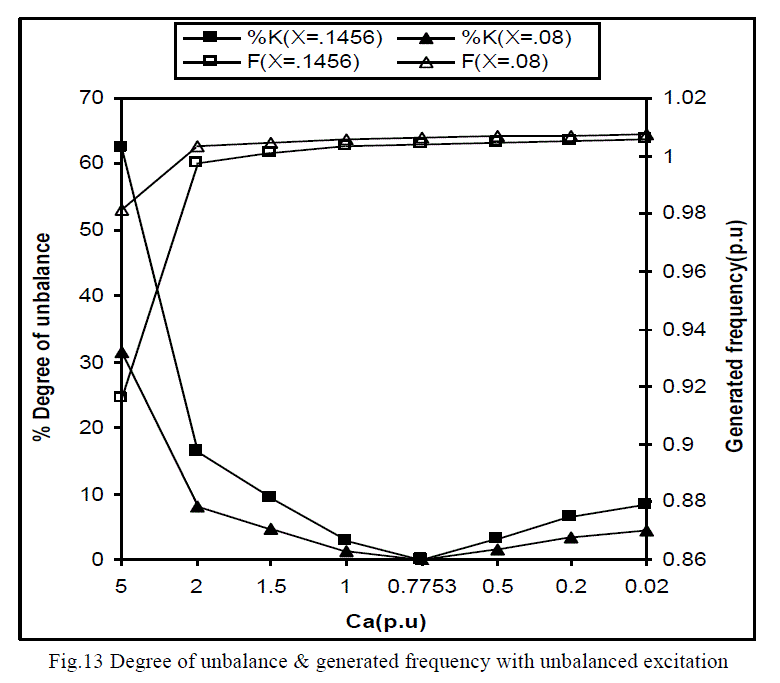
From Fig.13 it has been observed that change in excitation from both the sides (opened to short circuit) results in to a larger degree of unbalance as compared to the change across the load. Furthermore by reducing the value of reactance of stator & rotor side, results in to lower degree of unbalance and higher will be the generated frequency.
image
image
image

CONCLUSION
In this paper a new model based upon load decoupling across machine terminals has been proposed to study the effects of machine parameters on its performance during unbalanced operations. The model incorporates the magnetizing branch in negative sequence network and has been analyzed using symmetrical component approach. Simulated results as obtained shows the importance of machine leakage reactance to limit the voltages & currents during unbalance. Study may be used to design the parameters of machine, to be operated under safe operations.

References













APPENDIX-I
Machine-1:
3-phase, 15KW, 4-pole, 50 Hz, 415V, 30A, Delta connected squirrel cage induction machine with per-phase equivalent circuit parameters in per unit are as:
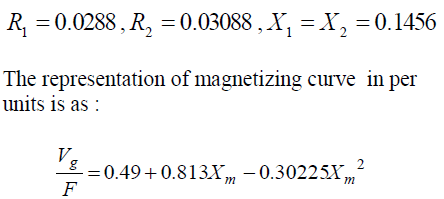image