International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Efficient Hashing Algorithm for Midsquare

Nitisha Rajgure1 and Dr Vilas Thakare2
  1. Assistant Professor, Dept. of Computer Science, Sipna COET, SGBAU, Amravati University, Maharastra, India
  2. Professor & Head, Dept. of Computer Science, SGBAU, Amravati University, Maharashtra, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Hashing function is the One of the most frequent way for finding the nearest match in the large data sets. From the last decades number of researcher has been work on the hashing and focusing on the better approach than the existing one with respective their performance. In this paper presents a survey on different type of hash functions, different type of hashing method, hashing strategies and structural weakness of them or the limitation of them that in which kind of problem they are suitable and what they can’t be used., also we are investigating the alternative approach for the mid- square hashing approach. The necessary data structures and algorithms are described, the expected performance is analyzed mathematically, and actual execution times are obtained and compared with alternative techniques. It shows that it provides the faster response time. Finally our method is intuitive and easy to implement.

Keywords
Hashing, algorithmic, access methods, data structures.

INTRODUCTION
The address computation can be implemented in several ways in the hash table , here we discuss its basic operations and typical hash function operations and the problem for which hash table are suitable and for which hash table are not suitable. Focus on the some common hashing methods, folding methods and other hashing method Mid square, Digit Addition, Analysis which are used in different application of Hashing. The necessary data structures and algorithms are described, the expected performance is analyzed mathematically, and actual execution times are obtained and compared with alternative techniques.
Hash defines “to hash” as “to chop up, as of potatoes”. This is exactly what hash functions usually do. A good hash function creates disorder and, in this way, avoids collisions.

OBJECTIVES
Finding the address of element from the hash table is one of the important task for performance of any algorithm. This function can be done by Hash-fictions.
The some existing algorithms is complicated to implement and the constant of the space bound is large. With focus of time and space bound ,We also study our opportunistic data structure in a dynamic setting and devise a variant achieving effective search and update time bounds. The focus objective of this study is to reduce the computational time of the Hashing function. Here we propose new algorithm as NKRSQR Hashing function with the following objectives.
NKRSQR Algorithm should be easy to implement and easy to Understand.
NKRSQR Algorithm Must Return the result with minimum time complexity.

RELATED WORK
Schmidt and Siegel [1] proposed the first algorithm for constructing a MPHF with constant evaluation time and description size O(n + log log u) bits..From a practical point of view, the algorithm of Schmidt and Siegel is not attractive.
The scheme is complicated to implement and the constant of the space bound is large. Ji, Jianqiu;Li, Jianmin et al [2] introduce an effective method, i.e. the min-max hash method, which significantly reduces the hashing time by half, yet it has a provably slightly smaller variance in estimating pair wise Jaccard similarity. In addition, the estimator of minmax hash only contains pair wise equality checking, thus it is especially suitable for approximate nearest neighbor search. Experiments show that with the same length of hash code, min-max has reduces the hashing time to half as much as that of min-wise hash. The divide-and-concatenate technique cannot speed up software implementations but can only improve the collision probability beyond that provided by the processor architecture. This is because, if a processor supports w-bit additions and multiplications in one or two cycles, then w/2-bit operations will also consume the same number of cycles as w-bit operations.[2].Abutaha, M.Hamamreh, R.[3] Introduce The new one way hash algorithm designed by using two steps. Firstly, convert the input data into matrix system by using all necessary conversions to generate the initial hash value. Secondly, use the output of the first step to make a digest for these data and finally generate the secure hash value. Joseph Gil and Yossi Matias implements the simple fast parallel hashing by oblivious Execution. This algorithm was design with bucket approach in data structures . Experimental result presents a simple fast and efficient parallel algorithm for the hashing problem Using n processors and the running time of the algorithm is O(lg lg n). More recently, Hagerup and Tholey [4] have come up with the best theoretical result we know of. The MPHF obtained can be evaluated in O(1) time and stored in n log e + log log u + O(n(log log n)2/ log n + log log log u) bits. The construction time is O(n+log log u) using O(n) words of space. Again, the terms involving u are negligible. In spite of its theoretical importance, the Hagerup and Tholey [4] algorithm is also not practical, as it emphasizes asymptotic space complexity only. (It is also very complicated to implement. Hashingbased approximate nearest neighbor (ANN) search in huge databases has become popular due to its computational and memory efficiency[5].

PROPOSED ALGORITHM
From the literature review we can conclude that the well deep knowledge of different data structure allows us to implement and design new algorithm which can fallow the basic principal of root data structure. The two principal criteria use in selecting a hash function;
- It should be very easy and quick to compute.
- Function should, return value with minimum number of collisions.
and the next section also describes how address can be computed from the keys using the hash function. Several variation on the basic theme are presented and analyzed; Focused line is that hashing is extremely effective and practical technique. Question is that How easy is it to design a hash function? It is quite easy , as a little number theory will help us prove.
A. Working Principal :
NKRSQR is based on the Divide and merge technique. This technique consist of decomposing the instance and merge as individual element for problem solving.
Two questions that naturally spring to mind are:
1.Why would any one want to do this?
2.How should we solve ?
First we partition the number ‘n’ in ‘Two’ slots by taking the remainder of ‘n’. That is the first step is computing as –
V1(n)= n mod 10--------------------eq(1)
V2(n)= n / 10--------------------------eq(2)
In second step apply the quadratic equation to find the square of number. Next Step can be done by extracting k bits from the middle of the square of the key.
H(n)= (v1+v2)2 >>(w-n)----------------eq(3)
NKRSQR follows nature of recursive algorithm. This Algorithm does a pretty good job as compare to middle –square method when the integer valued keys are equi-probable.
B. Address Space for Result Number:
The middle of square (or Mid- Square for short) function , fm is computed by squaring the identifiers and then using an appropriate number of bits from middle of the square to obtain the bucket address.Since the middle bit of the square will usually depend upon all of the characters’ in the identifier, it is expected that different identifiers would result in different hash addresses with high probability even when some of the characters in the identifiers are the same.
The number of bits to be used to obtain the bucket address depend on the table size . if n bits are used to compute hash address, the range of value is 2n , so the size of hash table is chosen to be a power of 2 when this kind of scheme is used .
MSHA(A)= n number of middle digits of (A2)
Where,
MSHA=Mid Square Hash Address

NKRSQR ADVANTAGES AND DISADVANTAGES
As earlier we note the phrase of universe , now we will discusses the some advantages and disadvantages of NKRSQR Hash function, This algorithm run faster than the existing one. However this is limited upto number 99 only.

NKRSQR RESULTS
The proposed energy efficient algorithm is implemented with basic programming of Algorithm. We tested output result with numbers from 1 to 99 for different size and required time . Proposed algorithm is compared with the basic traditional Mid-square hash function for address mapping . We considered the time and memory space , and processor execution time is calculated through the CPUTIME function of the program . proposed algorithm provides better complexity with respective time and space which is a need of computer era for speedup the process and maximum storage.
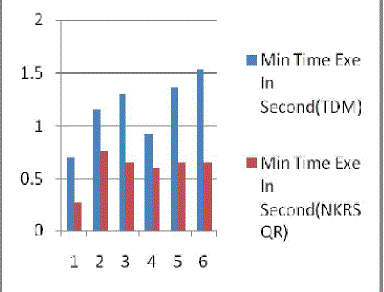
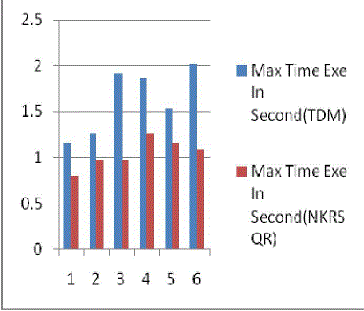
The result Fig. 1 shows the Traditional Vs New(NKRSQR) approach for min time. In the same way Fig 2 shows Traditional Vs New(NKRSQR) approach for Max time. Table 1. shows the Result Using Traditional Method of Time and memory usage while Table 2 shows Result Using (NKRSQR) Method , which defines the better execution time.
The results shows in Fig 1 of Traditional Vs New(NKRSQR) approach for min time ,that the proposed algorithm performs better with the minimum running time of this implementation is much less than the the traditional Midsquare hash function.
The results shows in Fig 2 of Traditional Vs New(NKRSQR) approach for Max time ,that the proposed algorithm performs better with the Maximum running time of this implementation is much less than the the traditional Midsquare hash function.
The Table 1 shows the Minimum and maximum time required time for Traditional approach of hash squring method .
The Table 2 shows the Minimum and maximum time required time for NKRSQR approach of hash squring method .

CONCLUSION AND FUTURE WORK
The results showed that the proposed algorithm performs better with the running time of this implementation is much less than the the traditional Mid- square hash function. The proposed algorithm provides better complexity with respective time and space which is a need of computer era for speedup the process and maximum storage. As the performance of the proposed algorithm is analyzed with only traditional Mid- square approach in hashing functions in future with some modifications in design considerations the performance of the proposed algorithm can be compared with other efficient algorithm. NKRSQR is the simplest hash function which is obtain by combination of two different method that is Division hash function and squaring hash function.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1 Figure 2
Figure 1 Figure 2
 

References