International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Efficient Path Finding Algorithm for Mobile Data-Gathering in Wireless Sensor Networks

M.Tamilarasi1, G.Yogarajan2 and T.Revathi2
  1. PG Scholar, Department of Information Technology,Mepco Schlenk Engineering College, Tamilnadu, India.
  2. Senior Professor and Head, Department of Information Technology, Mepco Schlenk Engineering College, Tamilnadu, India.
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

A new mobile data-gathering mechanisms for wireless sensor networks proposed in this paper. The mobile collector, called MobCar in this paper, directly visits all sensors and collects data by single hop from it. Since data packets are directly gathered without relays and collisions, the energy consumption on data gathering reduces. But data gathering latency is high. To overcome this problem a greedy approach based new mobile data gathering mechanisms are being proposed. Here, Path finding algorithm is used to find the polling points which directly collects the data from its neighbors. A MobCar visits each polling point and collects the data from them then forwards it to the sink node thus reducing the data gathering latency and energy consumption on data gathering and hence lifetime of the network gets increased. For the large scale applications, we consider utilizing multiple MobCars and propose a path finding algorithm where multiple MobCars traverse through several shorter subtours concurrently to satisfy the distance/time constraints. We carry out extensive simulations and the results demonstrate that our proposed algorithms can greatly shorten the moving distance of the MobCars compared with the travelling salesman problem.

Keywords
Wireless sensor networks (WSNs), data gathering, mobile data collector, MobCar, movement planning, spanning tree, travelling salesman problem (TSP).

INTRODUCTION
RAPID advances in the technology of wireless sensor networks (WSN) have led to its incorporation in a variety of applications, such as environment monitoring, event detection and target tracking. [1], [2]. WSNs consist of a large number of sensor nodes, which are battery powered tiny devices. These sensors perform three basic tasks: sense a physical quantity from the surrounding environment, process the acquired data and transfer them through wireless links to a data collection point called sink node or base station. The energy of a sensor is consumed on two major tasks: Sensing the environment and uploading data to the base station. In homogeneous network, Sensors sense the data and then forwards it to the sink node in one hop communication. If the distance between the sensor and sink is larger, it consumes large amount of energy for data transmission, since the data will be transmitted through several relay nodes, which has to relay many packets from sensors far away from the data collector. As a result, after these sensors fail, other sensors cannot reach the data collector and the network becomes disconnected, although most of the nodes can still survive for a long period. Therefore we introduced mobility into the network for data gathering such that MobCar is perfectly suitable for such applications.
A MobCar starts a data gathering tour from the data sink, travels an entire network, collects sensing data from nearby nodes while moving and uploads data to the data sink. It significantly reduces energy consumption at sensor nodes compared to commonly used multi-hop forwarding approach, thus prolonging network lifetime. However, a fatal drawback due to the use of a MobCar is increasing the latency of data gathering in WSN. In order to decrease the latency of data as gathering, the traveling path length of a MobCar must be shortened. Use of a Mobcar for collecting data in the wireless sensor network involves creating a path along which the MobCar can retrieve all data from all sensors while minimizing overall travel costs. In this paper we propose a path finding algorithm for planning the shortest moving path of Mobcar such that the data can be gathered from all sensors in that network with minimum length. For large scale sensor networks we use multiple MobCars for data gathering in that network.

RELATED WORKS
Here, we briefly outline some related works on the data-gathering schemes in WSNs. Data gathering schemes in WSNs can be roughly classified into three categories. Efficient relay routing, Hierarchical infrastructure and mobile data gathering. In the following, we briefly discuss some typical schemes in each category.
In the first category, the data packets are forwarded by sensors to the base station by using relay nodes. Scagline and Servetto [3] and Macro et al. [4] described joint data compression and routing in a WSN. It reduces the amount of raw data by utilizing the fact that data compression and forward to the sink by relays. Therefore relay nodes need to relay many packets from sensors far away from the data collector. As a result, the relay nodes get failed faster than other nodes, such that the data cannot be able to reach data sink.
In the second category, a WSN was organized into a hierarchical infrastructure for better scalability in which sensors are organized into clusters which is lower layer of the network and cluster head is higher layer of the network. Cluster head gather sensing data from sensors in corresponding clusters and forward data to the outside data sink [5], [6]. However, in such network cluster heads consume much more energy than other sensors. Therefore sensors can become cluster heads rotationally to avoid ―hot spots‖ [4]. Since every sensor node may possibly become a cluster head, each of them has to be ―powerful‖ enough to handle incoming and outgoing traffic which increases the overall cost of the sensor network. Furthermore, it may incur high overhead due to frequent exchange of information among sensors.
In the third category, the mobile data gathering schemes have been proposed in [7], [8], [9], [10], [11] to overcome these problems in static hierarchical networks. In such schemes a special type of mobile collector introduced in network for data gathering. Based on the mobility pattern, we can be further divided mobile data gathering schemes into two subclasses. Uncontrollable mobility and controlled mobility. In the following, we briefly discuss some typical schemes in each subclass. In the first subclass, the mobile collector either moves randomly or along a fixed track. [7] Described a type of mobile collectors, called data mules with random mobility in sparsely distributed sensor network. Data mules moves random path, gather data from nearby sensors, buffer the data and then drop them off to a sink. This scheme substantially reduces the amount of energy consumption at sensors, but its random moving path is difficult to manage and packet delay cannot be controlled. In the second subclass, the mobile collectors can freely move to any location in the network and its path can be planned. In [9] and [10], public transportation vehicles were adopted as mobile collectors. It describes sensor networks deployed in an urban area, public transportation vehicles such as buses and trains, which always move along fixed routes, can be attached with transceivers to act as mobile base stations. Compared with randomly moving data mules, the moving path and timing predictable in this case. However, data gathering routes and schedules of public transportation is very restrictive. To obtain more flexible data collecting paths for mobile collectors, Ma and Yang [11] proposed a moving path planning algorithm for mobile collector by a divide and conquer method. It recursively determines the turning point for load balancing and organizes each part of the network into a cluster. Ma, Zhao and Yang [12] presented a mobile data gathering scheme with SDMA technique, where mobile collector called SenCar equipped with two antennas. During data gathering tour, it collects data from two sensors when it comes close to the transmission range of sensors. It reduces the data uploading time but increases the moving time of the SenCar. Therefore data gathering latency increases. Ma and Yang [13] proposed mobile data gathering in wireless sensor networks with bounded relay hop. It selects subset of sensors will be as polling points that buffer locally aggregated data with bounded relay hop and upload the data to the mobile collector when it arrives. The advantage of this method is it reduces data gathering latency at the cost of buffer overflow due to more number of relay nodes. From the preceding discussions, we can see that various data gathering schemes in WSNs. In this paper we propose new mobile data gathering mechanisms which reduce both energy consumption and data gathering latency.

PRELIMINARIES
In this paper, we consider the mobile data gathering in wireless sensor networks. A MobCar can visit the transmission range of every static sensor, such that sensing data can be gathered by single hop communication without any relays and collisions. Before we describe the data gathering schemes, we first define some terms that will be used in the rest of this paper.
A. Candidate polling points
The transmission range of omnidirectional antenna was disk shaped area around the transceiver. Based on this assumption, the neighbor set of sensor consists of all sensors within the disk shaped around this sensor. If we know the one-hop neighbors of every sensor in the network, the position of each sensor can be a candidate polling point. If we don’t know the one hop neighbors of sensors in the network, the candidate polling points can be obtained by after sensors are deployed one or more MobCars need to explore the entire sensing field. While exploring, each MobCar can broadcast ―Hello‖ messages periodically with the same transmission power as sensors.
Each sensor decode the ―Hello‖ messages correctly sends with an ―ACK‖ message to notify the MobCar where it is. After receiving the ―ACK‖ message from the sensor, the Mobcar marks its current location as a candidate polling point and adds the ID of the sensor into the neighbor set of this candidate polling point. Additionally, during the neighbor discovering phase, each sensor can also discover its one-hop neighbors by broadcasting the ―Hello‖ messages. The sensor reports the IDs of its one-hop neighbors to the Mobcar by including the information into the ―ACK‖ message, after that the position of the sensor can also become a candidate polling point in the network.
Fig. 1, an example of neighbor discovery is illustrated. In the figure, the neighbors of MobCar finding by passing ―Hello‖ and ―ACK‖ between MobCar and sensor.
Image
In summary, a candidate polling point set can contain two types of points in the network: the positions where sensors are deployed and the points where the MobCar has tested the wireless links between it and its one-hop neighbors. After the discovering phase, each sensor has knowledge of all its one-hop neighbors and the Mobcar acquires the information about the neighbor set of each polling point in the network.
B. Polling points
Here, we consider the problem of finding the polling points from the candidate polling points. A MobCar polls nearby sensors one by one to gather data during data gathering phase. Upon receiving the polling message, a sensor simply uploads the data to the MobCar directly without relays and collisions. We define the positions where the MobCar polls sensors as polling points.
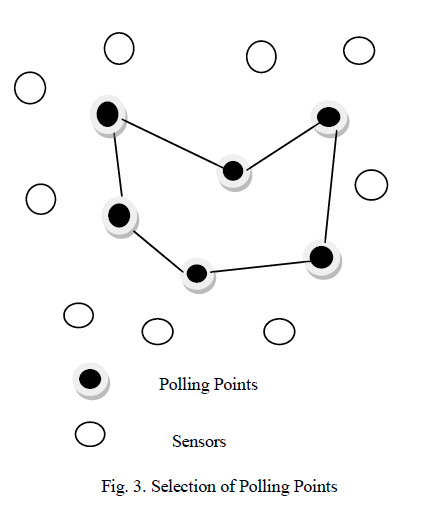Image
When a MobCar moves to a polling point, it polls nearby sensors with the same transmission power as sensors, such that sensors that receive the polling messages can upload packets to the MobCar in one hop. After gathering data from sensors around the polling point, the MobCar moves directly to the next polling point in the tour. Thus, each data gathering tour of a MobCar consists of a number of polling points and the straight line segments connecting them. For example, let PT= {pt1, pt2 . . . ptn} denote a set of polling points and DS be the data sink. Then, the moving tour of the MobCar can be represented by DS → pt1 → pt2 →・ ・ ・→ptn→ DS. Thus, the problem of determining the optimal tour can be considered as the problem of finding the locations of polling points and the order to visit them. Before a MobCar starts a data-gathering tour, it needs to determine the positions of all polling points and which sensors it can poll at each polling point.
In Fig. 3, illustrates an example of polling point selection problem. In the figure polling points selected from the network then MobCar collected data from polling points without any relays and collisions which covers all sensors.

DATA GATHERING WITH SINGLE MobCar
In small scale wireless sensor networks, the data can be collected by single MobCar. A MobCar could be a mobile robot or a vehicle equipped with a powerful transceiver, battery and large memory. The MobCar starts a data gathering tour from the data sink, traverse an entire network, and collects the sensed data from polling points
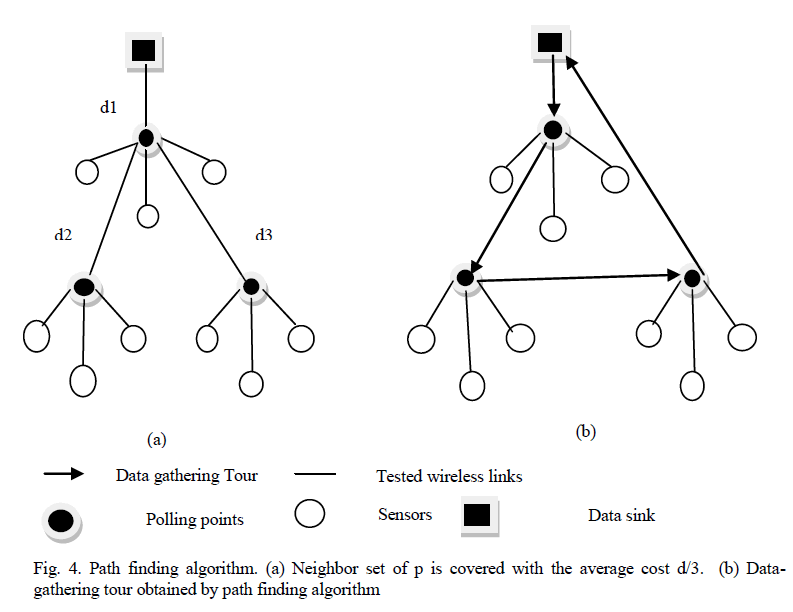Image
While moving and uploads data to the sink node. Path finding algorithm is used to find the polling points from the candidate polling points and then plan the datagathering tour of a single MobCar.
The data gathering tour starts from the sink node followed by the selection of polling point from the candidate polling points by using α value which is described by (1).
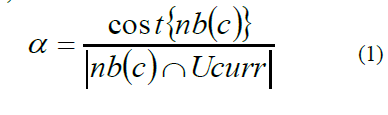Image
The value of α is the ratio of cost which is nothing but distance cost{nb(c)} between source and candidate polling points to the number of neighbors covered by candidate polling points nb(c). Finally, the candidate polling points with minimum α value will be selected as polling point.
The basic idea of proposed path finding algorithm with single Mobcar is to find a polling point from the candidate polling points and its corresponding neighbor set of sensors can be covered in the data-gathering tour at each stage. The algorithm will terminate after all sensors are covered. The algorithm tries to cover each uncovered neighbor set of sensors with the minimum average cost at each stage. It can be described as follows. Let PL curr be the set of all polling points, C contain set of all candidate polling points, and UC curr be the set of remaining uncovered sensors at each stage of the algorithm. Calculate the x and y coordinate of each sensor in the network and stored into the set of x [], y [].The neighbor set of each candidate polling point stored into the set of nb(c). The number of neighbors of each candidate polling point is stored into the set of non(c). Let α=cost {nb(c)}/|nb(c) ∩UCcurr|, which denotes the average cost to over all uncovered sensors in nb(c). The polling point is chosen from candidate polling points with minimum α value. Remove the polling points from UCcurr and added into PLcurr. Remove neighbor set of polling points nb(c) from UCcurr. The algorithm terminates when all sensor nodes are covered in the network. After finding the polling points, the minimum data gathering tour can be obtained by using Travelling Sales man Problem.
In Fig. 4, MobCar chooses p1 as the first polling point, since it can cover its neighbor nodes which is uncovered with minimum average cost d1/3. After that, p2 and p3 will be selected as the second and third polling points with the average cost d2/3 and d3/3, respectively. Finally, the shortest tour can be approximated on all chosen polling points and the data sink by using TSP [14].

Path finding Algorithm with Single MobCar
Image
Image
Image
Image

DATA GATHERING WITH MULTIPLE MobCars
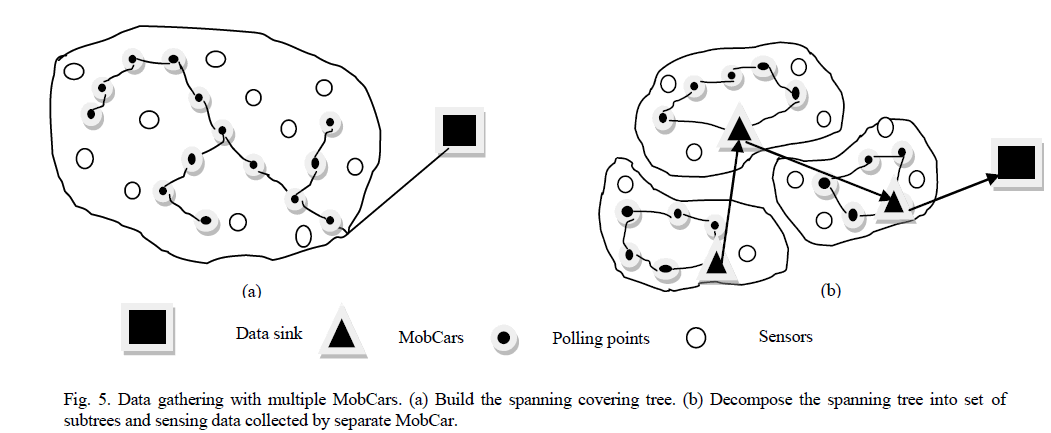
We have considered how to find the data-gathering tour of a single MobCar for small-scale applications. However, for some large-scale applications, a single MobCar cannot be able to visit the transmission ranges of all sensors in the network before their buffers overflow, such that each data-gathering tour may take a long time. A possible solution to this problem is to allow some sensors to relay packets from other nodes to the Mobcar. Thus, the MobCar need not to visit the transmission range of every single sensor in the network, and the length of each data gathering tour can be reduced. However, the drawback of using relay sensor nodes is that it may fail faster than other sensor nodes. To avoid unbalanced network lifetime, we will use one-hop data-gathering scheme with multiple MobCars.
In large scale applications, an entire network is divided into subnetwork. Separate Mobcar is assigned for each subnetwork and it is responsible for collecting data from that network. Once in a while, the MobCar forwards the gathering data to one of the other nearby MobCar, when two MobCars move closes enough. Finally, data can be forwarded to the MobCar that will visit the data sink via relays of other MobCars. Path finding algorithm with multiple MobCars is used to plan the subtours of multiple MobCars to minimize the data gathering length. It can be described as follows. First, select the polling points from candidate polling points by running the path finding algorithm. Let PL curr be the set of all polling points that found by using path finding algorithm with single MobCar. Then, find the minimum spanning tree TR (V, E) on polling points [15]. Let Dmax be the upper bound on the length of any subtour, which guarantees the data to be gathered before sensors run out of storage.
Note that Dmax could depend on a lot of factors, such as the data acquisition rate of sensors, the buffer size and the moving speed of MobCars. Let tr(v) denotes the subtree of TR, which is rooted at vertex v and consists of all child vertices of v and edges connecting them in TR. Let Parent {v} is the parent vertex of v in TR.
Let Weight {v} represents the sum of all link costs in the subtree tr(v) rooted at v. Then, calculate the weight values of all vertices in TR. Repeatedly remove subtrees from TR until no vertex is left in TR. To build a subtree tr in each stage, start from the deepest leaf vertex of the remaining TR, and let it be the root Root(tr) of the subtree tr. Check the weight of Parent(Root(tr)), and let Root(tr) = Parent(Root(tr)) if Weight(Parent(Root(tr))) ≤ Dmax/2. Otherwise, add all child vertices of Root (tr) and edges connecting them in TR into tr and remove tr from TR. Here, Weight (Parent (Root (tr))) also denotes the total edge length of subtree tr. After removing the subtree, upgrade the weight value of each vertex in the remaining TR. The algorithm terminates when TR is empty. Then TR is decomposed into a set of subtrees. The total length of any subtree tr, which is denoted by Dtr, is no more than Dmax/2. Finally, the subtour on polling points of each subtree can be determined by using the TSP.

Path finding Algorithm with Multiple MobCars
Step 1: Find the Polling point set PL.
Image
B. Results and Discussions
Extensive simulations were conducted to evaluate the performance of the proposed algorithms. In this section, the simulation results presented as below. We first compare the tour length of a single MobCar obtained by running the path finding algorithm with the tsp.
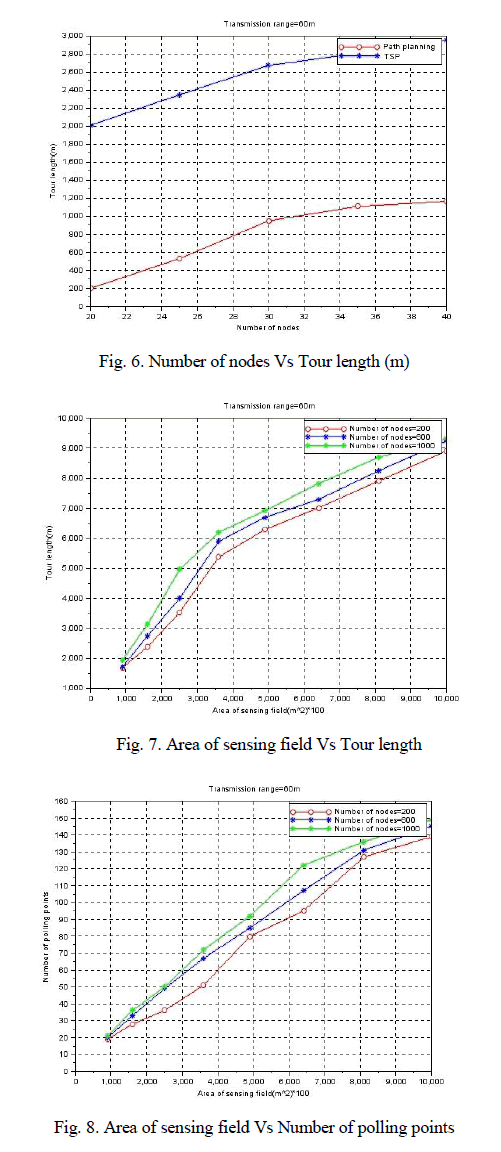
Fig.6 plots the average tour length for transmission range equal to 60 m and the number of sensors equal to 20, 30, and 40. Fig. 6 shows that the tour length of the proposed algorithm is lesser than the tsp. Fig. 7 and 8 plots the performance of path finding algorithm for all combinations of Number of nodes equal to 200, 600, and 1000 and the area of sensing field equal to 300 m * 300m to 1000 m * 1000 m. Fig. 7 shows that the tour length increases with increase in the area of sensing field.
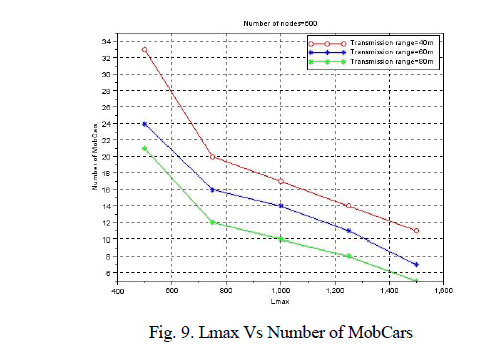Image
Image
Fig. 8 shows that the Number of polling points increases with the increase in the area of sensing field. Fig. 9 plots the performance of path finding algorithm with multiple MobCars for all combinations of transmission range equal to 40, 60, 80 m and the Lmax equal to 500 to 1500. Fig. 9 shows that the Number of MobCars decreases with the increases in the Lmax.

CONCLUSION AND FUTURE WORK
In this paper, we proposed a mobile data-gathering mechanism for wireless sensor networks. We introduced a mobile collector, called MobCar, which works like a mobile base station in the network. Here we proposed a path finding algorithm is used to find polling points. A MobCar starts the data-gathering tour periodically from sink node visits each polling point and collects the data from them which covers all sensors and then forwards it to the sink thus reducing the data gathering latency and energy consumption and hence lifetime of the network gets increased. For large scale sensor networks, we introduced multiple MobCars by letting each of them move through a shorter subtour than an entire tour. The simulation results demonstrate that our proposed datagathering mechanisms can greatly shorten the moving distance compared with the Travelling salesman problem. In addition, it can prolong the network lifetime compared with the static data collector and mobile data collector that can only move along a straight lines. As a possible direction for future research, we planned to find the minimum tour length by employing evolutionary computing techniques like Genetic Algorithm (GA), Ant Colony Optimization (ACO) to improve the performance than the proposed path finding algorithm.

References
  1. A. Mainwaring, J. Polastre, R. Szewczyk, D. Culler, and J. Anderson, ―Wireless sensor networks for habitat monitoring,‖ in Proc. ACM IntWorkshop Wireless Sens. Netw. Appl., Atlanta, GA, Sep. 2002, pp. 88–97.
  2. L. Schwiebert, S. K. S. Gupta, and J. Weinmann, ―Research challenges in wireless networks of biomedical sensors,‖ in Proc. ACM MobiCom, 2001, pp. 151–165.
  3. Scaglione and S.D. Servetto, ―On the Interdependence of Routing and Data Compression in Multi-Hop Sensor Networks,‖Proc. MobiCom, 2002.
  4. D. Marco, E.J. Duarte-Melo, M. Liu, and D. Neuhoff, ―On the Many-to-One Transport Capacity of a Dense Wireless Sensor Network and the Compressibility of its Data,‖ Proc. Int’l conf. Information Processing in Sensor Networks (IPSN), Apr. 2003.
  5. W.R. Heinzelman, A. Chandrakasan, and H. Balakrishnan, ―Energy- Efficient Communication Protocol for Wireless Micro sensor Networks,‖ Proc. Hawaii Int’l Conf. System Sciences (HICCS), Jan. 2000.
  6. X. Liu, J. Cao, S. Lai, C. Yang, H. Wu, and Y. Xu, ―Energy efficient clustering for WSN-based structural health monitoring,‖ in Proc. IEEE INFOCOM, Apr. 2011, pp. 2768–2776.
  7. R. Shah, S. Roy, S. Jain, and W. Brunette, ―Data MULEs: Modeling a Three-Tier Architecture for Sparse Sensor Networks,‖ Elsevier AdHoc Networks J., vol. 1, pp. 215-233, Sept. 2003.
  8. P. Juang, H. Oki, Y. Wang, M. Martonosi, L. Peh, and D. Rubenstein, ―Energy-efficient computing for wildlife tracking: Design tradeoffs and early experiences with Zebra Net,‖ in Proc. ASPLOS, 2002, pp. 96–107.
  9. Chakrabarty, A. Sabharwal, and B. Aazhang, ―Using predictable observer mobility for power efficient design of a sensor network,‖ in Proc.2nd Int. Workshop IPSN, Apr. 2003, pp. 129–145.
  10. Pentland, R. Fletcher, and A. Hasson, ―Daknet: Rethinking connectivity in developing nations,‖ Computer, vol. 37, no. 1, pp. 78–83, Jan. 2004.
  11. M. Ma and Y. Yang, ―SenCar: An Energy-Efficient Data Gathering Mechanism for Large-Scale Multihop Sensor Networks,‖ IEEE Trans. Parallel and Distributed Systems, vol. 18, no. 10, pp. 1476-1488, Oct. 2007.
  12. M. Zhao, M. Ma, and Y. Yang, ―Mobile Data Gathering with Space-Division Multiple Access in Wireless Sensor Networks,‖ Proc. IEEE INFOCOM ’08, Apr. 2008.
  13. M. Zhao and Y. Yang, ―Bounded relay hop mobile data gathering in wireless sensor networks,‖ IEEE Trans. Comput., vol. 61, no. 2, pp. 265–277, Feb. 2012.
  14. S. S. Skiena, ―Traveling salesman problem,‖ in The Algorithm Design Manual. New York: Springer-Verlag, 1997, pp. 319–322.
  15. M. Ma, Y. Yang and M.Zhao, ―Tour Planning for Mobile Data – Gathering Mechanisms in Wireless Sensor Networks,‖ IEEE Trans. Vehicular tech., vol. 62, no. 4, pp. 1472–1483, May. 2013.
  16. The Network Simulator NS-2. [Online]. Available: http://www.isi.edu/nsnam/ns.