International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Electromagnetic Fields in Tissue- Equivalent Liquids for Different Frequencies by Means of Flux Density

Khitam Y. El wasife1, Amal Y. Al Batniji2
 Department of Physics, Islamic University Of Gaza, P.O. Box 108, Gaza, Palestinian Authority1, 2
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

It is possible to use the dielectric parameters (effective permittivity and equivalent conductivity) of tissue equivalent liquids to evaluate electric and magnetic field for different electromagnetic wave frequencies . The electric and magnetic field in tissue equivalent liquids has been evaluated by means of flux density. Electromagnetic waves with different frequencies has been simulated used the finite difference time domain method . Found that the electric field amplitude decrease by increasing the frequency. The results reveal many interesting properties for measuring specific absorption rate.

Keywords
electromagnetic waves- Tissue equivalent liquid-FDTD-flux density

INTRODUCTION
The daily exposure of hundreds of thousands of people to electromagnetic fields of electromagnetic waves intensity is without precedent, much concern and interest has been expressed in the possibility, that there could be associated health risks. Biological effects due to radio wave exposure are dependent on frequency [1-2]. Excitation was provided in the model by assuming a electromagnetic waves modal structure or static field distribution. The structure under test was taken to be a homogeneous cube with permittivity and conductivity equal to that of muscle tissue. Additional work on an engineering design approach of the electromagnetic waves cell using the finite-element method was reported in [3]. The dielectric properties of tissue are determined by a number of dispersion phenomena which are described[4]. Additional, lower frequency, dispersions are known to exist but have little bearing at microwave frequencies, however, excellent reviews have been provided by Pethig [5-6]. Specific absorption rate is generally obtained by measuring the electric field in a phantom made of a shell filled with a tissue-equivalent liquid.Based on the dielectric characteristics of the human body, such as the permittivities and conductivities of various tissues, and further investigations [7]. Tissue equivalent materials have a variety of uses, including routine quality assurance and quality control in both diagnostic and therapeutic physics. They are frequently used in a research capacity to measure doses delivered to patients undergoing various therapeutic procedures. However, very few tissue equivalent materials have been developed for research use at the low frequencies . Derived limits in terms of power flux density or in terms of electric field strength E (V/m) and magnetic field strength H (A/m) has been derived [8]. At operating frequencies of mobile communications base stations in far-field conditions, the measurement of the electric field strength is sufficient. A simple equation described the correlation to power flux density. K. Fukunaga et al evalued the time dependence of dielectric properties of tissue-equivalent liquids recommended in the standard documents, and found that the permittivity and the conductivity decrease with time due to the evaporation of water [9]. Development of a Liquid-Type Human-Body Equivalent Antenna Using NaCl Solution has been investigated . NaCl solution for tissue-equivalent liquid filled in the humanequivalent antenna because NaCl solution is easy to prepare and is often used for tissue-equivalent liquid. The relative permittivities and conductivities of NaCl solution were measured with a coaxial cell (National Physical Laboratory, UK). The applicable frequency of the coaxial cell is from 15MHz to 1GHz . Different substances have been used as tissue-simulating materials [10-14]. Of these, the sugar-based liquids described in [10] are common because they have low toxicity and are easy to obtain. For these liquids, sugar (sucrose) is used to lower the permittivity of water and sodium chloride is added to increase the conductivity. In this study, common granulated cane sugar, salt (NaCl), and deionized water were used In this paper, the form of flux density useied to evaluate the electric and magnetic field simulated in a tissue equivalent liquids as diethylen glycol monobuthyl . FDTD method has been used to determine electric and magnetic field for different frequencies .

II. THEORY AND MODEL
Figure 1 shows source of electromagnetic waves as sinusoidal waves with determine frequency. The source is at distance 30 cm from the boundary of The mixture of de-ionized water diethylene glycol monobuthyl ether (DGBE) [9]. Diethylene glycol monomethyl ether (DGME) is a colorless liquid at room temperature with a mild, ether-like odor. It is highly soluble (miscible) in water. This product is manufactured by the reaction of methanol and ethylene oxide. Its Applications is a good solvent for many classes of dyes including basic chrome, naphthol, and stabilized reduced vat dyes.
in this study. Tables 1 show the target values and the recipes recommended in the standard [15], for 900, 1450, 1950, and 2450 MHz
We use the form of flux density into the simulation. Its importunacy is apparent in problem of frequency dependent materials. Maxwell's equation in firm of flux density are
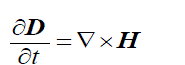image      (1)
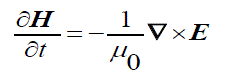image      (2)
where J=σ.E is the current density, and
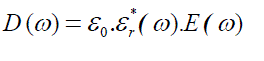image      (3)
We assume the dielectric properties of tissue are donated with the complex permittivity ε*r
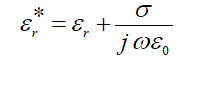image    (4)
where ε*r is the real relative part of the permittivity, σ is the conductivity and ω is the radial frequency of the signal[ 16 ].
Substituting equatiin (4) in (3) ,then
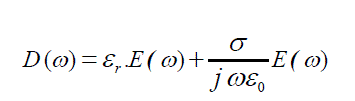image    (5)
Taking the first term into the time domain is not problem, because it is simple multiplication. In the second term. Fourier theory tells us that 1/jω in the frequency domain is integration in the time domain ,so equation (5) becomes[16].
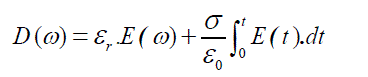image    (6)
The integral approximated as a summation over the time steps Δt are
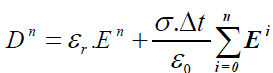image    (7)
we solve for En given the value of Dn , so separating the En term from the result of summation
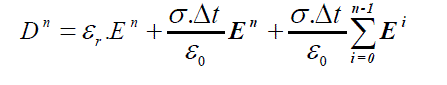image    (8)
The electric field En can be written as
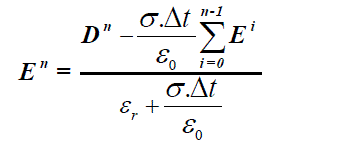image    (9)
Choose the new parameter as
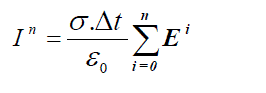image    (10)
Substituting in equation (9) we have
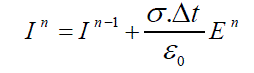image    (11)
At every time steps n , simply adds the value En times the constant term to the previous values of the summation n-1. The dielectric properties for four frequencies are illustrated in table (1)

III. RESULTS AND DISCUSSION
The electric and magnetic fields have been calculated numerically. The finite-difference time-domain (FDTD) method is used to evaluates the electric and magnetic field for different value of permativity and conductivity of tissue equivalent liquid. It is methods of numerical analysis. The mixture of deionized water diethylene glycol monobuthyl ether (DGBE)has been used . We have been change the formulation slightly and introduce the use of flux density into the simulation.

IV. CONCLUSION
For different electromagnetic wave frequencies . The electric and magnetic field in tissue equivalent liquids has been evaluated by means of flux density. It has been simulated useing the finite difference time domain method (FDTD) . Found that the electric field amplitude decrease by increasing the frequency. The results of this research reveal many interesting properties for measuring specific absorption rate.
The Benefits of DGME has low odor and high solvency and can fill a wide range of solvent requirements.

ACKNOWLEDGMENT
This research is supported partially by the Islamic university Research Program of Gaza. I would like to thank Professor Dr. mohammed shabat (Department of Physics. Islamic university of Gaza is gratefully discussed for the using FDTD method in this research

Tables at a glance
Table icon Table icon Table icon Table icon Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
 

References
  1. O. P. Gandhi, "Use of the Finite-Difference Time-Domain Method for Calculating EM absorption in Man Model, "IEEE Trans. on Biomed. Vol. 35, No. 3, pp.179-186, 1998.
  2. O. P. Gandhi, J.-Y. Chen and A. Riazi, "Currents Induced in a Human Being for Plane-Wave Exposure Conditions 0-50 MHz and for RF Sealers, "IEEE Trans. Biomed. Eng.Vol.33, No. 8, pp.757- 767, 1986.
  3. Cai-XD and Costache-GI, “An engineering design approach of a triple- TEM cell using finiteelement method,” IEEE Trans. Electromag. Compat., vol. 16, no. 4, pp. 189–195. 1974.
  4. RAICU, V, KITUGAWA, N and IRIMAJIRI, A.: „A quantitative approach to thedielectric properties of skin, Physics in medicine and biology,Vol. 45, No. 2, pp. 1-4. 2000 .
  5. PETHIG, R.: „Dielectric properties of body tissues, Clinical physics and physiological measurements, Vol. 8, pp. 5 – 12,1987 .
  6. PETHIG, R.: „Dielectric properties of biological materials: biophysical and medical applications, IEEE trans. Electrical Insulation, Vol.19,No. 5, pp 474-435 . 1984.
  7. A. Drossos, V. Santomaa and N. Kuster: "The dependence of electromagnetic energy absorption upon human head tissue composition in the frequency range of 300-3000 MHz", IEEE Trans. Microwave Theory Tech., Vol. 48, No. 11 pp. 1988 - 1995. 2000.
  8. Wolfgang Müllner, Georg Neubauer, and Harald Haider "Guidelines for Limiting Exposure to Time-Varying Electric, Magnetic, and Electromagnetic Fields (up to 300 GHz)," Health Physics Vol. 74, No. 4 pp. 494522. 1998.
  9. K. Fukunaga, S. Watanabe, Y. Yamanaka,"Optimisation of tissue-equivalent liquids for SAR measurements", Progress in Electromagnetic Research Symposium Pisa, Italy,Vol.65, pp. 28– 31,2004.
  10. G. Hartsgrove, A. Kraszewski, and A. Surowiec, “Simulated biological materials for electromagnetic radiation absorption studies,” Bioelectromagnetics. Vol. 8, pp. 29–36, 1987.
  11. C.-K. Chou, G. W. Chen, A. W. Guy, and K. H. Luk, “Formulas for preparing phantom muscle tissue at various radiofrequencies,” Bioelectromagnetics, Vol. 5, pp. 435–441, 1984.
  12. M. Kanda, M. Ballen, and C.-K. Chou, “Formulation and characterization of tissue simulating liquids used for SAR measurement (500–2000 MHz),” in Asia–Pacific Radio Science Conf., Tokyo, Japan, p. 274,2001.
  13. A. Peyman and C. Gabriel, “Tissue equivalent liquids for SAR measurement at microwave frequencies,” presented at the Bioelectromagnetics Society 24th Annual Meeting, Quebec, QC, Canada, P-53, 2002.
  14. V. Vigneras, “Elaboration and characterization of biological tissues equivalent liquids in the frequency range 0.9–3 GHz, final report,” PIOM Lab., Univ. Bordeaux, Bordeaux, France. 2001.
  15. IEC 106/24/CD "Methods for the assessment of electric, magnetic and elecromagnetic fields associated with human exposure". 2001 .
  16. Khitam El Wasife," Power density and SAR in multi-layered life tissue at Global system mobile (GSM) frequencies" Journal of Electromagnetic Analysis and Applications, Vol. 3, pp. 328-332, 2011.