ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
San San Tint1 , Htet Htet Win2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Cryptography provides a powerful means of verifying the authenticity of data and identifying the culprit. It plays vital role in many electronic applications. Information confidentially, authentication and integrity are desirable features for electronic transactions and these features are achieved by using a proper combination of symmetric and asymmetric cryptographic techniques. In order to ensure information authenticity, digital signatures are the equivalent part for normal signatures. Forgery of digital information can be identified with the help of digital signature. This paper intends to design secure electronic certificate and to control fake certificate for electronic learning system
Keywords |
| Asymmetric Cryptographic, Elliptic Curve, Digital Signatures, Electronic Certificate, Public Key Cryptography |
INTRODUCTION |
| As technology is advancing, creation of fake electronic certificates becomes easier. To identify these certificates, a method is proposed that utilizes the combination of hashing and signing techniques. As the objective is strong signatures that occupy minimal space on the certificate, Elliptic curve Digital signatures are considered for the proposed scheme. So public key cryptography, Elliptic curve Digital signature scheme and hash techniques are applied to the system. |
| ECDSA is a cryptographic scheme based on ECC. The Elliptic Curve Digital Signature Algorithm (ECDSA) is the elliptic curve analogue of the DSA. ECDSA was first proposed in 1992 by Scott Vanstone in response to NIST’s (National Institute of Standards and Technology) request for public comments on their first proposal for DSS. It was accepted in 1998 as an ISO (International Standards Organization) standard (ISO 14888-3), accepted in 1999 as an ANSI (American National Standards Institute) standard (ANSI X9.62), and accepted in 2000 as an IEEE (Institute of Electrical and Electronics Engineers) standard (IEEE 1363-2000) and a FIPS standard (FIPS 186-2). It is also under consideration for inclusion in some other ISO standards. In this paper, we describe the ANSI X9.62 ECDSA, present rationale for some of the design decisions, and discuss related security, implementation, and interoperability issues. Digital Signature Algorithm (DSA) is based on discrete logarithms. |
| The main objectives of this paper are (1) to create the signature and verification on issuing certificate (2) to control fake electronic certificate with the combination of hashing and signing technique (3) to enter the e-learning center only the person with the electronic certificate produced by administrator [1, 2]. |
BACKGROUND THEORY |
| The proposed scheme is based on public key cryptography, hash function and signature techniques. |
| 1. Public key crypto systems have a key pair called public and private keys used for encryption and decryption process. Information encrypted with a private key can be decrypted with corresponding inverse key called public key. This concept raised information authentication with digital signatures. A digital code can be attached to an electronically transmitted message that uniquely identifies the sender and ensures that the document has not been altered in any way, since the sender has signed it [3]. |
| 2. A digital signature is a term used for marking or signing an electronic document by a process meant to be analogous to paper signatures, but which makes use of a technology known as public-key cryptography. In other words, it's a digital code that can be attached to an electronically transmitted message that uniquely identifies the sender and ensures that the document has not been altered in any way, since the sender has signed it [4]. |
| 3. Hash functions take an arbitrarily long piece of plaintext and compute a fixed length hash value. Computing a message digest from a piece of plain text is much faster than encryption of same text, with the asymmetric crypto algorithms. By using message digest, speed of the signature generation and verification process is increased [5]. Hashing techniques are frequently used for message integrity and for the creation and verification of digital signatures. MD5 (Message Digest Algorithm) and SHA (Secure Hashing Algorithm) are two popular hashing algorithms used in security applications. In this Paper SHA-I algorithm is considered as; it generates 160 bits hash value [6]. |
| 4. The Elliptic Curve Digital Signature Algorithm (ECDSA) is the elliptic curve analogue of the Digital Signature Algorithm (DSA). It was accepted in 1999 as an ANSI standard, and was accepted in 2000 as IEEE and NIST standards. It was also accepted in 1998 as an ISO standard, and is under consideration for inclusion in some other ISO standards. Unlike the ordinary discrete logarithm problem and the integer factorization problem, no sub exponential-time algorithm is known for the elliptic curve discrete logarithm problem. For this reason, the strength-perkey- bit is substantially greater in an algorithm that uses elliptic curves. This paper describes the ANSI X9.62 ECDSA, and discusses related security, implementation, and interoperability issues [1-5]. |
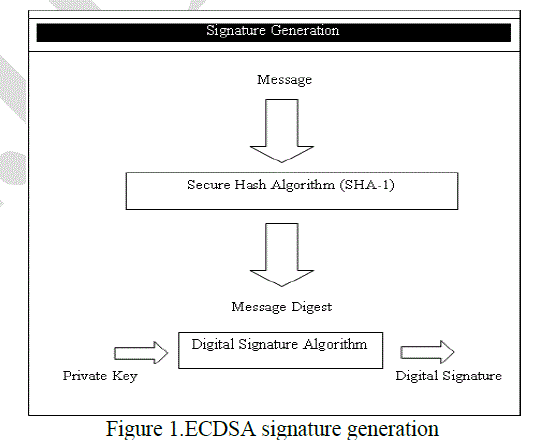
| 5. ECDSA Signature Generation |
| To sign an information m, an entity A with the domain parameters D = (q, a, b, G, n) and associated key pair (Q, d) [4]. Where d and Q represents public and private keys and a, b represents the coefficients of the elliptic curve. G is a point on the curve. n is the order of the elliptic curve (y2 = x3 + ax + b mod (n)). |
| 1 . Select a random integer k, where 1 <= k <= n-1. |
| 2. Compute kG = (x1, y1) and convert x1 to an integer x1bar. |
| 3. Compute r = x1 mod n, if r = 0 go to step 1. |
| 4. Compute k-1 mod n. |
| 5. Compute SHA-1(m) and convert this bit string to an integer e. |
| 6. Compute s= k-1(e + dr) mod n. if s=0 then go to |
| step 1. |
| 7. A’s signature to the message m is (r, s) |
| In figure 1, the proposed system digest the message using secure hash algorithm SHA-1 and digested message will be a digital signature using digital signature algorithm and a public key. |
 |
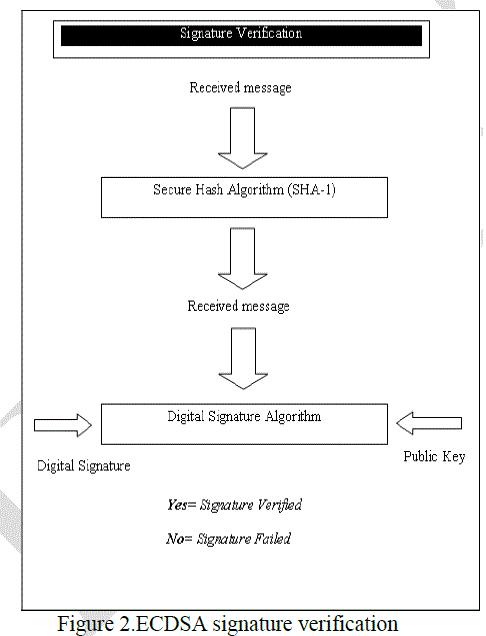
| 6. ECDSA Signature Verification |
| To verify A’s signature (r, s) on m, B obtains a required copy of A’s domain parameters D = (q, a, b, G, n) and associated public key Q. |
| 1. Verify that r and s are integers in the interval [1,n-1]. |
| 2. Compute SHA-1 (m) and convert this bit string to an integer e. |
| 3. Compute w = s-1 mod n. |
| 4 . Compute u1 = ew mod n and u2 = rw mod n. |
| 5. Compute X = u1G + u2Q. |
| 6. If X = 0, then reject the signature. Otherwise convert the x-co-ordinate x1 of X to an integer x1bar, and compute v = x1bar mod n. |
| In figure 2, detail flow for ECDSA signature verification is described. In this paper, secure hash algorithm SHA-1 an digital signature algorithm are used to have more secured the proposed system. |
 |
PROPOSED SYSTEM |
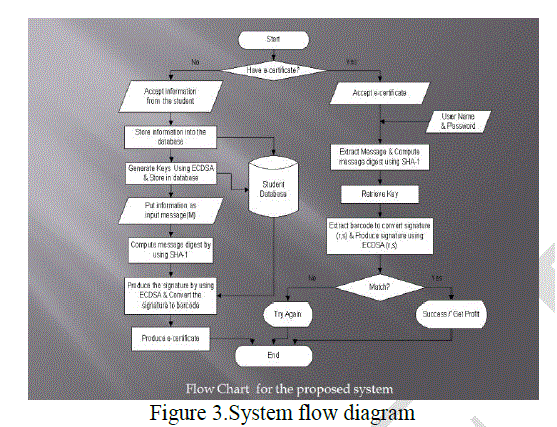
| In this section a method is described to generate/verify the signature pertaining to the information. It is assumed that the certificate issuing authority, obtained digital certificates from proper channel, and the public key of the issuing authority is available to all concerned. The proposed system aims not only to be secure electronic learning system but also to prevent from unauthorized users’ access and fate certificate. |
 |
| Notations |
| The following notations are used throughout the paper. |
| • Msg denotes the user input. |
| • H denotes the hash algorithm (SHA-1). |
| • Sign denotes the signature algorithm (ECDSA). |
| • BC denotes the barcode of certificate. |
| •MD1 denotes user message digest within certificate. |
| •MD2 denotes message digest to compare with MD1. |
| • ASC denotes the ASCII code. |
| •Verify denotes the verification process using public key. |
| 1. Creation of Signature on the Issuing Certificate |
| The variable unique information pertaining to the candidate, to whom certificate is issued, (first name, middle name, last name, Father’s name, year of university and role) has to be considered as an input m. |
| 1. Input message is hashed with the Secure Hashing algorithm (SHA-I) to create a hash value. |
| 2. Hash value is signed using the private key of the issuing authority to create digital signature. |
| 3. The signature value is converted into a barcode BC and printed along with the information required on the certificate. |
| The following equation explains the creation of signature on certificate. |
| BC(Sign[H(Msg)])+Msg=Certificate |
| 2. Verification of the Certificate |
| 1. Msg and BC are split from Certificate to make verification process. |
| 2. Msg is hashed with the secure hashing algorithm (SHA-1) to create hash value MD1. |
| 3. BC is converted into ASCII code and it is verified with the public key of the issuing authority, which gives a value MD2. |
| 4. Compare the values MD1 and MD2. Certificate is treated fake if MD1 does not match with MD2 otherwise it is original. |
| MD1=H(Msg) |
| MD2= Verify (ASC (BC (Sign [H(Msg)])) ) |
EXPERIMENTAL RESULTS |
| This system intends to be secure electronic learning system and to prevent the unauthorized access using fate certificate. This scheme consists of three processes (1) user registration (2) certificate generation and (2) certificate verification at login process. |
| 1. User Registration |
| If a user is a new user, he/she must register firstly. This user needs to input his/her information and generate public/private key pair. This user information and private key will be used to create electronic certificate. The user registration process is displayed in Figure 4. Web structure mining discovers useful knowledge from hyperlinks (or links for short), which represent the structure of the Web. For example, from the links, discovering important Web pages, which, incidentally, is a key technology used in search engines. Communities of users who share common interests can also be discovered. Traditional data mining does not perform such tasks because there is usually no link structure in a relational table. |
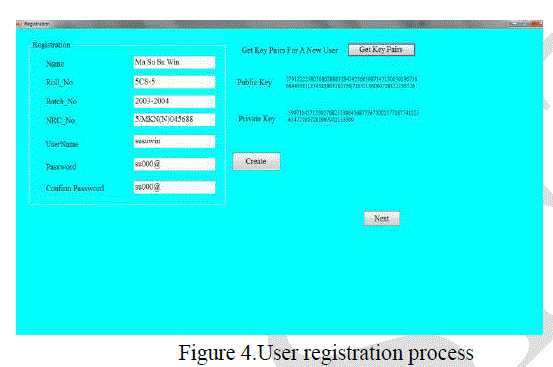 |
| In figure 4, The user needs to fill his or her information such as name, roll number, academic year, National identity card and so on. |
| 2. Certificate Generation |
| The generation of certificate using ECDSA algorithm is shown in Figure 5. |
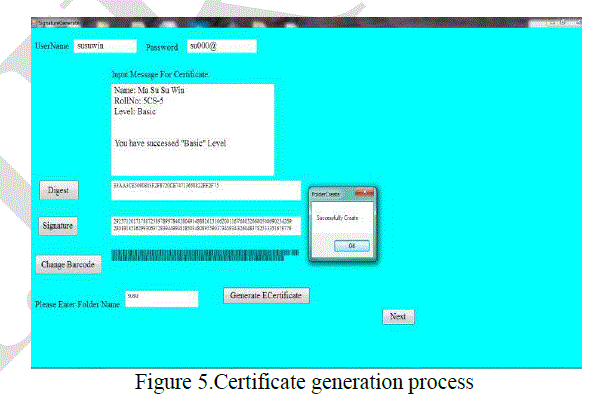 |
| In this process, the input message from user is hashed into message digest. This digest code is encrypted into signature value using ECDSA algorithm. The signature value is converted into barcode. The user input message and barcode are combined into electronic certificate. |
| 3. Certificate Verification |
| If user is already a member, this user must put an electronic certificate. When the certificate is received, the verification process is performed as shown in Figure 6. |
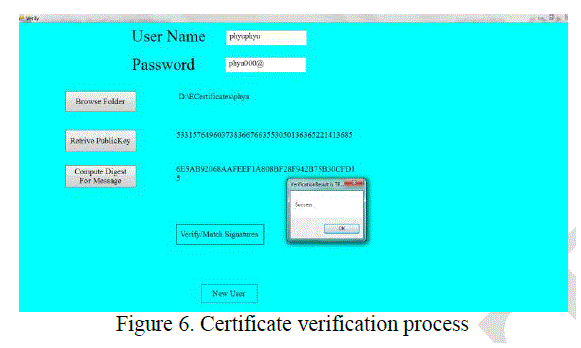 |
| If the verification process success, user will be allowed to enter to electronic learning center. Otherwise, the user fails in login request. |
CONCLUSION |
| In order to control fake certificates, a method is proposed by utilizing digital signatures. As RSA related signatures demand more space, Elliptic curve based signatures are considered for this method. The combination of Elliptic curve (ECDSA) and SHA-1 algorithm provides strong cryptographic strength and optimizes the computational speed as well as space. In future work, the certification authority (CA) will be designed between user and server for the purpose of trusted third party system and to get more secure client-server authentication system. |
References |
|