ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Rene Thomas1 and Sushitha Susan Joseph2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Security is a state of being free from danger or threat. When someone finds the vulnerabilities and loopholes in a system without permission means the system lacks its security. Wherever a secure data sharing occurs between multiparty there would be the possibility for undesirable attacks. In a variety of application domains such as patient medical records, military applications, social networking, electronic voting, business and personal applications there is a great significance of anonymity. Using this system we can store our data as groups and also encrypt it with encryption key. Only the privileged person can see the data. The secure computation function widely used is secure sum that allows parties to compute the sum of their individual inputs without mentioning the inputs to one another. This function helps to characterize the complexities of the secure multiparty computation. Another algorithm for sharing simple integer data on top of secure sum is built. The sharing algorithm will be used at each iteration of this algorithm for anonymous ID assignment (AIDA). By this algorithm and certain security measures it is possible to have a system which is free from undesirable attacks.
Keywords |
| Vulnerability, anonymity, encryption key, secure multiparty computation, AIDA |
INTRODUCTION |
| Nowadays security in multiparty data sharing is one of the most inevitable element. The emendation of undesirable attacks with AIDA algorithm and privacy preserving communications etc. are based on an assumption that each party is semi-honest. Internet involves and enables sharing of data but identity of the shared data owner is to be preserved. This is called maintaining anonymity that is quite difficult with increasing server storages like cloud, a problem area. Researchers have also investigated the relevance of anonymity and/or privacy in various application domains: patient medical records [1], electronic voting [2], e-mail [3], social networking [4], etc. |
| Defining privacy-preserving data access turns out to be harder than you might expect, because many superficially attractive definitions break down. Some definitions work if the analyst can ask only one question, but get into trouble if the analyst can ask multiple questions the analyst might be able to ask two harmless questions whose answers, taken together, reveal everything about an individual. Some definitions break down if the analyst has any access to outside information about the world, even basic information like the fact that the average human is less than ten feet tall. Some definitions turn out to be impossible to achieve in this universe. Differential privacy avoids all of these pitfalls. |
| The core of the definition is simple but subtle. Imagine two data sets, A and B, which are exactly identical except that A includes information about one additional person who is not included in B. Now we ask: If we let the analyst get answers to questions about our data set, can the analyst tell whether we are using data set A or data set B? If the analyst canâÃâ¬ÃŸt tell the difference and this result holds no matter which data set A we started with and no matter which person we excluded from B, then we have succeeded in preserving privacy. Why? Because any inference the analyst makes about you will have to be the same inference he would have made even if your information were not in the data set at all. To put it another way, including your information in the data set did nothing to harm your privacy. So whatever may be the things security is essential without the any default. |
| The main algorithm is based on a method for anonymously sharing simple data and results in methods for efficient sharing of complex data. a. There are many applications that require dynamic unique IDs for network nodes [5]. The IDs are needed in networks for security or for administrative tasks requiring reliability, such as configuration and monitoring of individual nodes, and download of binary code or data aggregation descriptions to these nodes. It further explores the connection between sharing secrets in an anonymous manner, distributed secure computation and random ID assignment. The network is not anonymous and the participants are identifiable in that they are known to and can be addressed by the others. This paper builds an algorithm for sharing simple integer data on top of secure sum. |
RELATED WORK |
| The existing system has many advantages and disadvantages. Existing and new algorithms for assigning anonymous IDs are examined with respect to trade-offs between communication and computational requirements. Also, suppose that access to the database is strictly controlled, because data are used for certain experiments that need to be maintained confidential. Clearly, allowing one person to directly read the contents of the tuple breaks the privacy of another; on the other hand, the confidentiality of the database managed by first is violated once second has access to the contents of the database. Thus, the problem is to check whether the database inserted with the tuple is still kanonymous, without letting oneâÃâ¬ÃŸs and second know the contents of the tuple and the database respectively. The current system has certain algorithms the secure sum allows us to share simple data anonymously even if it does not have enough security measures we are adding the anonymous data sharing power sums algorithm and finally we got a system which can send complex data but as it names signifies itself it is difficult to find the ways in which how it is arranged and further modification are also not possible. For the convenience of the system we are adding AIDA algorithm it is easy to send complex data but the data are not all secure and even a hacker can easily read the data and a cracker can easily change the contents. |
| Consider, group of hospitals (or any system which you want to share details) desire to share the average of data items by means of individual databases. Nodes contain data items and workout and allocate only the total value. Along with some assurances of anonymity, a secure sum algorithm permits the sum to be collected. To allocate the nodes identifiers, numbers ranging from 1 to N, was applied in the technique and the identities received are unidentified to the other members of the group and in that this assignment is anonymous. The semi-honest model of privacy preserving data mining was assumed, in which each node will go after the rules of the protocol, however may possibly use the information it spots during the implementation of the protocol to compromise security.To solve this problem, we use the secure um algorithm which is as follows: |
 |
 |
| Each algorithm compared can be reasonably implemented and each has its advantages. Our use of the Newton identities greatly decreases communication overhead.This can enable the use of a larger number of “slots” with a consequent reduction in the number of rounds required. The solution of a polynomial can be avoided at some expense byusing SturmâÃâ¬ÃŸs theorem. All of the non-cryptographic algorithms have been extensively simulated, and we can say that the present work does offer a basis upon which implementations can be constructed. The communications requirements of the algorithms depend heavily on the underlying implementation of the chosen secure sum algorithm. In some cases, merging the two layers could result in reduced overhead. |
EXPERIMENTAL RESULTS |
| The system using AIDA algorithm, it is easy to transfer complex data anonymously without any interference. For this we are having an admin or someone who can add the members and those want to participate in the data sharing. The system mainly deals with the efficient algorithms for assigning identifiers (IDs) [6] to the nodes of a network in such a way that the IDs are anonymous using a distributed computation with no central authority. |
| The Fig 1 of ideal system builds an algorithm for sharing simple integer data on top of secure sum. The sharing algorithm will be used at each iteration of the algorithm for anonymous ID assignment (AIDA). This AIDA algorithm, and the variants that we discuss, can require a variable and unbounded number of iterations. With the help of this system explores the connection between sharing secrets in an anonymous manner, distributed secure multiparty computation and anonymous ID assignment. |
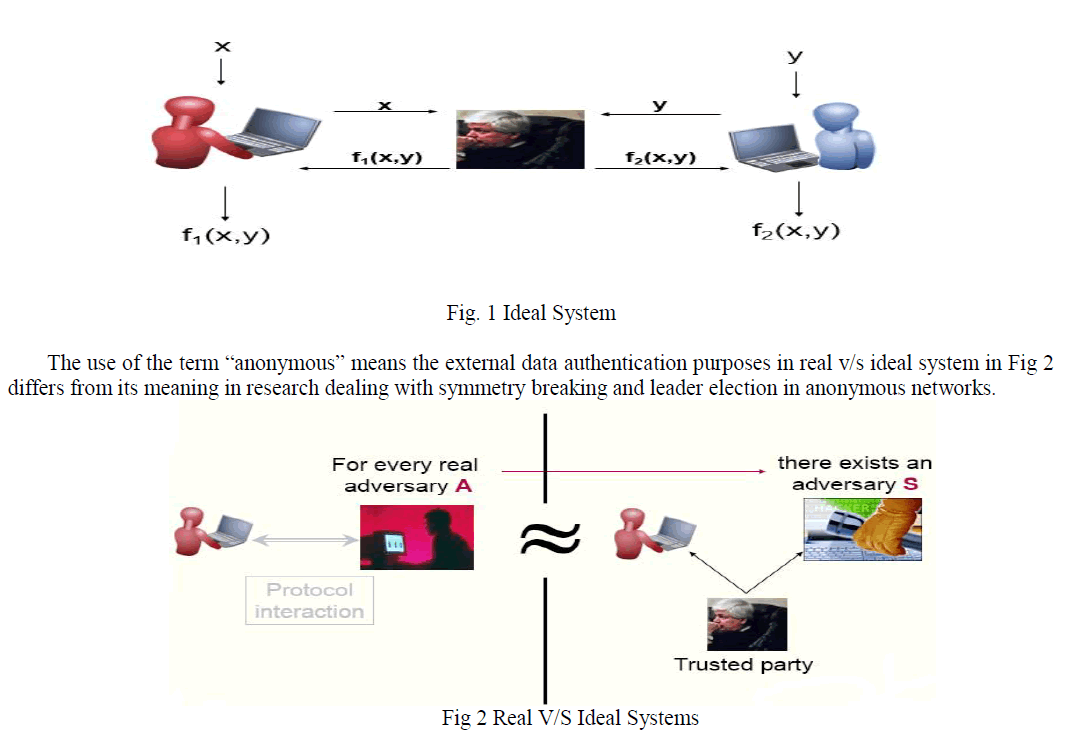 |
| Our network is not anonymous and the participants are identifiable in that they are known to and can be addressed by the others. Methods for assigning and using sets of pseudonyms have been developed for anonymous communication in mobile networks. The methods developed in these works generally require a trusted administrator, as written, and their end products generally differ from ours in form and/or in statistical properties. |
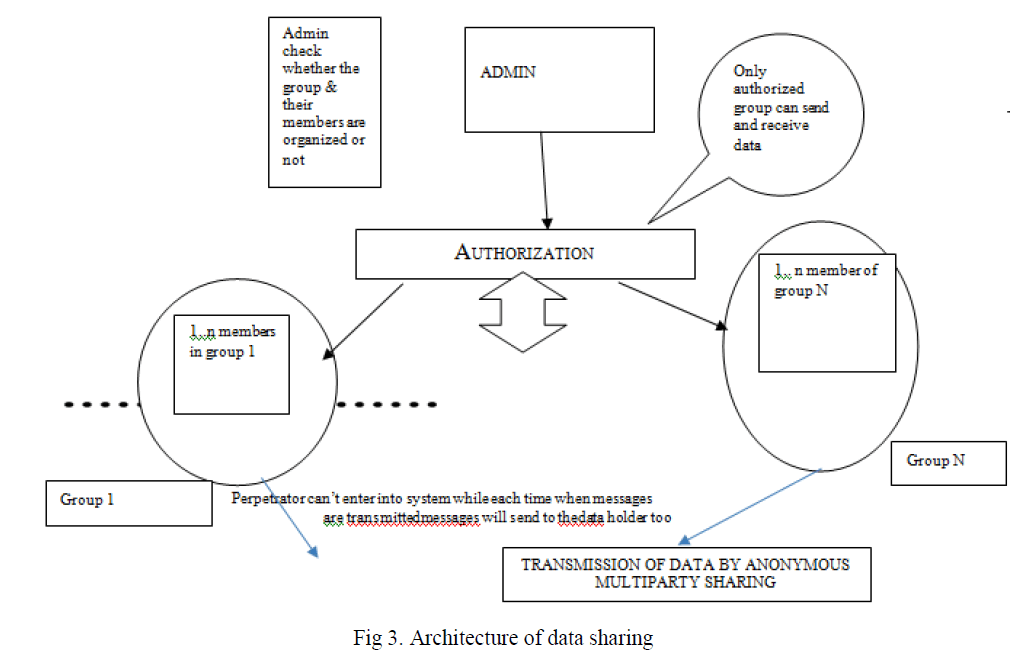 |
| Fig 3 explains that increasing a parameter in the algorithm will reduce the number of expected rounds.Every members have anonymous id and they are known to the trusted third party. Suppose trusted third party say T, and admin say Main (M). If the group A need to send information to some members in „iâÃâ¬ÃŸ groups. Each group have separate authentication, where the admin whether the groupâÃâ¬ÃŸs authorized or not. Just like an authorization module for checking the password invalid or not. If it is an authorized group the One Time Password (OTP) will be generated and that generate did will be given to the group which we need to send, if these groups are also authorized. Then they were able to send information between them.After accessing the group id using OTP the message code will be generated. Then these message code will reached their appropriate destination. So that the message received by each member will be transferring required data as far as possible. Since each of the group can be send message only if they are authorized and for receiving message also it would be an authorized group. This is how the proposed system improves its security. Simultaneously the messages will received by multiple members. Even though every members in the group does not need the entire information the id will provide the appropriate message if those idâÃâ¬ÃŸs are matching. This is how the anonymous id generated and adding some additional security measures and all the undesirable attacks in the multiparty data sharing with AIDA algorithm will be possible. |
CONCLUSION |
| The proposed system AIDA rule is the main thing in allocating ID to users and therefore the anonymous identity is maintained within the user and therefore the information owner isn't compromised below any circumstances therefore providing ample proof for the sets of users in multiparty environments. The anonymous identity is maintained in the user. The data owner is not compromised under any circumstances. Even under difficult situations the communications and bandwidth is not affected in any manner. AIDA proves to be secure for distributed architecture keeping the user safe from prying persons under attack in different segments. In future the scheme may be extended as a web service so that any interconnected user of the network can utilize it to the maximum without the need to implement the code. It is sure that an intruder can never enter into the system unless or until with help of centralized authority and then the message will send to all of the users who participating in this data sharing. Also mobile web services are an area of interest for future extensions to AIDA.Using this system we can ensure high security in all its aspects and many future enhancements can be done with the help of it. |
References |
|