Keywords
|
| privacy preservation, data anonymization, data publishing, data security. |
INTRODUCTION
|
| Government agencies and other organizations often need to publish microdata, e.g., medical data or census data, for research and other purposes. Typically, such data is stored in a table, and each record (row) corresponds to one individual. Each record has a number of attributes, which can be divided into the following three categories. (1) Attributes that clearly identify individuals. These are known as explicit identifiers and include, e.g.,Social Security Number. (2) Attributes whose values when taken together can potentially identify an individual. These are known as quasi-identifiers, and may include, e.g., Zip-code, Birth-date, and Gender. (3) Attributes that are considered sensitive, such as Disease and Salary. |
| When releasing microdata, it is necessary to prevent the sensitive information of the individuals from being disclosed. Two types of information disclosure have been identified in the literature [8], [15]: identity disclosure and attribute disclosure. Identity disclosure occurs when an individual is linked to a particular record in the released table. Attribute disclosure occurs when new information about some individuals is revealed, i.e., the released data makes it possible to infer the characteristics of an individual more accurately than it would be possible before the data release. Identity disclosure often leads to attribute disclosure. include both explicit identifiers and quasiidentifiers. |
FROM k-ANONYMITY TO l-DIVERSITY
|
| The protection k-anonymity provides is simple and easy to understand. If a table satisfies k -anonymity for some value k, then anyone who knows only the quasi-identifier values of one individual cannot identify the record corresponding to that individual with confidence greater than 1/k. |
| While k-anonymity protects against identity disclosure, it does not provide sufficient protection against attribute disclosure. This has been recognized by several authors, e.g., [23], [33], [40]. Two attacks were identified in [23]: the homogeneity attack and the background knowledge attack. |
| Example 1: Table 1 is the original data table, and Table 2 is an anonymized version of it satisfying 3-anonymity. The Disease attribute is sensitive. Suppose Alice knows that Bob is a 27-year old man living in ZIP 47678 and Bob’s record is in the table. From Table 2, Alice can conclude that Bob corresponds to one of the first three records, and thus must have heart disease. This is the homogeneity attack. For an example of the background knowledge attack, suppose that, by knowing Carl’s age and zip code, Alice can conclude that Carl corresponds to a record in the last equivalence class in Table 2. Furthermore, suppose that Alice knows that Carl has a very low risk for heart disease. This background knowledge enables Alice to conclude that Carl most likely has cancer. |
| 1) Distinct l-diversity. The simplest understanding of “well represented” would be to ensure there are at least l distinct values for the sensitive attribute in each equivalence class. Distinct l -diversity does not prevent probabilistic inference attacks. An equivalence class may have one value appear much more frequently than other values, enabling an adversary to conclude that an entity in the equivalence class is very likely to have that value. This motivated the development of the following stronger notions of l -diversity. |
| 2) Probabilistic l-diversity. An anonymized table satisfies probabilistic l -diversity if the frequency of a sensitive value in each group is at most 1/l this guarantees that an observer cannot infer the sensitive value of an individual with probability greater than 1/l |
| 3) Entropy l-diversity. The entropy of an equivalence class E is defined to be |
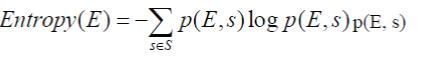 |
| in which S is the domain of the sensitive attribute, and p(E, s) is the fraction of records in E that have sensitive value s. |
| A table is said to have entropy `-diversity if for every equivalence class E, Entropy(E) ? log l `. Entropy l `- diversity is stronger than distinct `-diversity. As pointed out in [23], in order to have entropy ` l -diversity for each equivalence class, the entropy of the entire table must be at least log(l). Sometimes this may too restrictive, as the entropy of the entire table may be low if a few values are very common. This leads to the following less conservative notion of ` l -diversity. |
| 4) Recursive (c, l `)-diversity. Recursive (c, l )-diversity (c is a float number and l is an integer) makes sure that the most frequent value does not appear too frequently, and the less frequent values do not appear too rarely. Let m be the number of values in an equivalence class, and ri,,1 _ ? i ? m be the number of times that the ith most frequent sensitive value appears in an equivalence class E. Then E is said to have recursive (c, l `)-diversity if r1 < c(rl + rl+1 + ... + rm). A table is said to have recursive (c, l)-diversity if all of its equivalence classes have recursive (c, l)-diversity. |
LIMITATIONS OF ` l –DIVERSITY
|
| While the `-diversity principle represents an important step beyond k-anonymity in protecting against attribute disclosure, it has several shortcomings.l-diversity may be difficult to achieve and may not provide sufficient privacy protection. |
| Example 2: Suppose that the original data has only one sensitive attribute: the test result for a particular virus. It takestwo values: positive and negative. Further suppose that thereare 10000 records, with 99% of them being negative, and only1% being positive. Then the two values have very different degrees of sensitivity. One would not mind being known to betested negative, because then one is the same as 99% of the population, but one would not want to be known/considered to be tested positive. In this case, 2-diversity does not provide sufficient privacy protection for an equivalence class that contains only records that are negative. In order to have a distinct 2-diverse table, there can be at most 10000×1% = 100equivalence classes and the information loss would be large.Also observe that because the entropy of the sensitive attribute in the overall table is very small, if one uses entropy l - diversity, l must be set to a small value. l -diversity is insufficient to prevent attribute disclosure. |
| Below we present two attacks on l -diversity. Skewness Attack: When the overall distribution is skewed,satisfying `-diversity does not prevent attribute disclosure. |
ALGORITHM
|
| Step 1: Let P be a set of tuples is partitioned into r partitions {P1, P2, ..., Pr} |
| Step 2: If Pi (1 <= i <= r) contains at least n records, then Pi satisfies the (n, t)-closeness requirement. |
| Step 3: If Pi (1 <= i <=r) contains less than n records, the algorithm computes the distance between Pi and each partition in Parent (P). |
| Step 4: If there exists at least one large partition (containing at least n records) in Parent (P) whose distance to Pi (D [Pi,Q]) is at most t |
| Step 5: Pi satisfies the (n, t)-closeness requirement. |
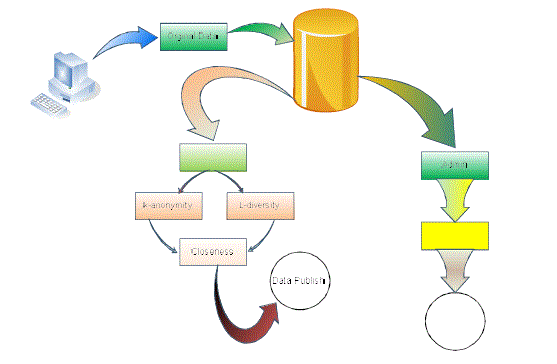
ARCHITECTURE OF THE PROPOSED SYSTEM
|
METHOD DESCRIPTION
|
| Admin |
| • While the released table gives useful information to researchers, it presents disclosure risk to the individuals whose data are in the table. |
| • Therefore, our objective is to limit the disclosure risk to an acceptable level while maximizing the benefit. |
| • This is achieved by anonym zing the data before release. |
| • The first step of anonymization is to remove explicit identifiers. |
| • However, this is not enough, as an adversary may already know the quasi-identifier values of some individuals in the table. This knowledge can be either from personal knowledge (e.g., knowing a particular individual in person), or from other publicly available databases (e.g., a voter registration list) that include both explicit identifiers and quasi-identifiers. |
| Survey |
| • GOVERNMENT agencies and other organizations often need to publish microdata, e.g., medical data or census data, for research and other purposes. |
| • Typically, such data are stored in a table, and each record (row) corresponds to one individual. |
| • Each record has a number of attributes, Which can be divided into the following three categories: |
| • 1) Attributes that clearly identify individuals. These are known as explicit identifiers and include, e.g., Social Security Number. |
| • 2) Attributes whose values when taken together can potentially identify an individual. These are known as quasi-identifiers, and may include, e.g., Zip code, Birth-date, and Gender. |
| • 3) Attributes that are considered sensitive, such as Disease and Salary. When releasing micro data, it is necessary to prevent the sensitive information of the individuals from being disclosed. |
| • Two types of information disclosure have been identified in the literature: identity disclosure and attribute disclosure. |
| • Identity disclosure occurs when an individual is linked to a particular record in the released table. Security |
| • The protection k-anonymity provides is simple and easy to understand. |
| • If a table satisfies k-anonymity for some value k, then anyone who knows only the quasi-identifier values of one individual cannot identify the record corresponding to that individual with confidence greater than 1=k. |
| • While k-anonymity protects against identity disclosure, it does not provide sufficient protection against attribute disclosure. |
| Privacy measure |
| • In this paper, we propose a novel privacy notion called “closeness.” |
| • We first formalize the idea of global background knowledge and propose the base model t-closeness which requires that the distribution of a sensitive attribute in any equivalence class to be close to the distribution of the attribute in the overall table. |
| • This effectively limits the amount of individual-specific information an observer can learn. However, an analysis on data utility shows that t-closeness substantially limits the amount of useful information that can be extracted from the released data. |
| • This limits the amount of sensitive information about individuals while preserves features and patterns about large groups. |
| • To incorporate distances between values of sensitive attributes, we use the Earth Mover Distance metric to measure the distance between the two distributions. |
| • We also show that EMD has its limitations and describe our desiderata for designing the distance measure. |
| Data publishing |
| • Privacy-preserving data publishing has been extensively studied in several other aspects. |
| • First, background knowledge presents additional challenges in defining privacy requirements. |
| • Second, several work considered continual data publishing, i.e., republication of the data after it has been updated. |
| • Presence to prevent membership disclosure, which is different from identity/attribute disclosure. Showed that knowledge of the anonymization algorithm for data publishing can leak extra sensitive |
CONCLUSION AND FUTURE WORK
|
| While k-anonymity protects against identity disclosure, it does not provide sufficient protection against attribute disclosure The notion of l`-diversity attempts to solve this problem. We have shown that l`-diversity has a number of limitations and especially presented two attacks on l-diversity. Thus we have proposed a novel privacy notion called “closeness” and a more flexible privacy model called (n, t)-closeness. We explain the rationale of the (n, t)- closeness model and show that it achieves a better balance between privacy and utility. To incorporate semantic distance, we choose to use the Earth Mover Distance measure. We also point out the limitations of EMD, present the desiderata for designing the distance measure, and propose a new distance measure that meets all the requirements. Finally, through experiments on real data, we show that similarity attacks are a real concern and the (n, t)- closeness model better protects the data while improving the utility of the released data. |
Tables at a glance
|
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
References
|
- C. Aggarwal, “On k-Anonymity and the Curse of Dimensionality,” Proc. of the Int’l Conf. on Very Large Data Bases (VLDB), pp. 901909,2005.
- G. Aggarwal, T. Feder, K. Kenthapadi, S. Khuller, R. Panigrahy, D. Thomas, and A. Zhu, “Achieving Anonymity via Clustering,” Proc. Of the ACM Symp. on Principles of Database Systems (PODS), pp. 153- 162, 2006.
- R. K. Ahuja, T. L. Magnanti, and J. B. Orlin, Network flows: theory, algorithms, and applications, Prentice-Hall, Inc., 1993.
- R. J. Bayardo and R. Agrawal, “Data Privacy through Optimal k- Anonymization,” Proc. Int’l Conf. Data Engineering (ICDE), pp. 217- 228,2005.
- F. Bacchus, A. Grove, J. Y. Halpern, and D. Koller, “From Statistics to Beliefs”, Proc. of National Conference on Artificial Intelligence (AAAI), pp. 602-608, 1992.
- J.-W. Byun, Y. Sohn, E. Bertino, and N. Li, “Secure Anonymization for Incremental Datasets,” Secure Data Management (SDM), pp. 4863,2006.
- B.-C. Chen, K. LeFevre, and R. Ramakrishnan, “Privacy Skyline: Privacy with Multidimensional Adversarial Knowledge,” Proc. of the Int’l Conf. on Very Large Data Bases (VLDB), pp. 770–781, 2007.
- G. T. Duncan and D. Lambert, “Disclosure-Limited Data Dissemination,” Journal of The American Statistical Association, vol. 81, pp. 10-28,1986.
- B. C. M. Fung, K. Wang, and P. S. Yu, “Top-down Specialization for Information and Privacy Preservation,” Proc. Int’l Conf. Data Engineering (ICDE), pp. 205216, 2005.
- C. R. Givens and R. M. Shortt, “A class of Wasserstein metrics for probability distributions,” Michigan Math Journal, vol. 31, pp. 231-240,1984.
|