Enhancement of Speech Signal by Adaptation of
Scales and Thresholds of Bionic Wavelet Transform Coefficients

Rupali Sharma; Preety D Swami

Enhancement of Speech Signal by Adaptation of Scales and Thresholds of Bionic Wavelet Transform Coefficients

Rupali Sharma¹, Preety D Swami²

Department of Electronics & Communication, Samrat Ashok Technological Institute, Vidisha,India
Department of Electronics & Instrumentation, Samrat Ashok Technological Institute, Vidisha,India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper proposes a speech signal enhancement method in which the wavelet transform scales and thresholds both are adaptive depending on the input noisy signal affected by Additive White Gaussian Noise (AWGN). The proposed Estimated Noise and Adaptive Threshold Bionic Wavelet Transform (ENAT-BWT) method analyses the incoming noisy speech signal at 22 scales, from 7 to 28, of the BWT for negative SNR levels and at 28 scales, from 6 to 33, of the BWT for positive SNR levels. Initially, the thresholds for various noise levels are determined manually that provide the best signal to noise ratios (SNR). Then, using curve fitting approach a generalized model is obtained that provides the best threshold parameter for input noisy signal of any noise standard deviation. Thus the algorithm selects the threshold value from the generalized model and soft thresholding is applied to the BWT coefficients. Finally, inverse bionic wavelet transform (IBWT) of thresholded BWT coefficients is computed which provides the enhanced speech signal. Results are measured using signal-to-noise ratio (SNR) and segmental signal-to-noise ratio (SSNR) for additive white Gaussian noise at various input SNR levels. Results are compared with variety of speech enhancement techniques, including BWT, PWT and Ephraim Malah filtering. Overall results indicate that SNR and SSNR improvements for the proposed approach are far superior than those of the techniques under comparison.

Keywords

Adaptive thresholding, Additive White Gaussian Noise, Bionic Wavelet Transform, Continuous Wavelet Transform, Speech enhancement.

INTRODUCTION

Speech is a common mode of communication. Using speech, we can communicate with each other. In many speech processing applications such as mobile communication, speech recognition, hearing aids etc, the degradation of the quality of speech signals due to addition of background noise is a common problem. Because of this we need to enhance the quality of speech signal to obtain a noise free signal. Speech enhancement is basically a speech denoising technique in which the goal is to remove the noise components present in the signal. There has been a lot of research in speech denoising so far, but, there always remains room for improvements. Different methods of speech enhancement are Spectral Subtraction [1], Wiener filtering [2], [3], Ephraim Malah filtering [4], [5], Wavelet transform [6], [7], [8], [9], etc. Wavelet transform techniques reduce computational complexity and achieve better noise reduction performance. Wavelet denoising techniques [10], perform noise reduction using thresholding. Basically, it can be divided into three steps. The first step is computing the coefficients of the wavelet transform (WT) which is a linear operation. The second step is thresholding of these coefficients which is a nonlinear operation. In the last step, inverse of thresholded coefficients is taken by applying inverse wavelet transform, which leads to the denoised signal. Wavelet coefficient thresholding technique is very simple and efficient.

In this paper, Estimated Noise and Adaptive Threshold Bionic Wavelet Transform (ENAT-BWT) technique is proposed as a denoising algorithm. In this technique, the noise standard-deviation (σˆ ) of the incoming noisy signal is to be estimated first. For this, the DWT of noisy speech signal is computed. Then, σˆ is computed as the median absolute deviation/.6745 of the wavelet coefficients belonging to the diagonal sub band coefficients. For negative SNR levels the BWT of noisy signal at 22 scales, from 7 to 28, is computed and for positive SNR levels the BWT of noisy signal at 28 scales, from 6 to 33, is computed. The thresholds for various noise levels are determined manually, that provide the best signal to noise ratios (SNR). Then, using curve fitting approach a generalized model is obtained that provides the best threshold parameter for input noisy signal of any noise standard deviation. Thus the algorithm selects the threshold value from the model and soft thresholding is applied to the BWT coefficients. Finally, inverse bionic wavelet transform (IBWT) of thresholded BWT coefficients is computed. This provides the enhanced speech signal. Results are compared with Bionic wavelet transform (BWT) [11], Packet wavelet transform (PWT) [9], and Ephraim Malah filtering technique [5].

The paper is organized as follows. Section II gives an overview of speech enhancement domains and various wavelet transforms. Section III introduces the proposed approach and outlines the experimental method. Section IV includes the criterion of evaluation and results of these experiments, followed by overall conclusions in Section V.

BACKGROUND

There are basically two domains of speech enhancement. First one is time domain approach and second one is transform domain approach. In time domain approach, filtering is performed directly on the time sequence. This includes techniques such as LPC based digital filtering, Hidden markov model (HMM), and Kalman filtering. In the transform domain techniques, signals are first transformed into a new domain and then noise attenuation is performed on the transformed coefficients. Such techniques are Fourier Transform (FT), Discrete Fourier Transform (DFT), Discrete Cosine Transform (DCT), Wavelet Transform (WT) etc. The time domain filtering of corrupted signal is simple methods and is beneficial only when removing high frequency noise from low frequency signals. However they do not provide satisfactory results under real world conditions.

Advantage of wavelet transform is that, wavelet analysis allows the use of long time intervals for low frequency information and shorter regions for high frequency information. In time domain we represent a function as a sum of weighted delta functions, whereas in frequency domain a function is represented as a sum of weighted sinusoids. In wavelet domain a function is represented as a sum of time-shifted (translated) and scaled (dilated) representation of some arbitrary function, which is called a wavelet. Broad categorization of wavelet transform comprise of the Continuous Wavelet Transform & the Discrete Wavelet Transform.

A. Continuous Wavelet Transform (CWT)

The continuous wavelet transform [6], is the sum for the overall time of the signal multiplied by scaled and shifted versions of the wavelet. The wavelet coefficients obtained are a function of scale and position. The CWT of signal x(t) is given by

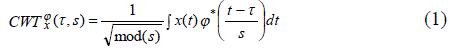Where τ and s are the translation and scale parameters respectively, and φ(t) is the mother wavelet chosen for the transform. The inverse transform also exists.

B. Discrete Wavelet Transform (DWT)

In discrete wavelet transform [7], scale and translation axis are based on powers of two so called dyadic scale and translation. The main advantage of DWT over CWT is that it is comparatively faster, easier to implement and avoids redundancy.

C. Wavelet Packet Transform (WPT)

Wavelet packet transform [8], [9], is generalization of the DWT and is also based on filter bank decomposition approach. In WPT the filtering of both low and high frequency components are performed, whereas in DWT the filtering of only low frequency components is performed.

D. Bionic Wavelet Transform (BWT)

The BWT is an asdaptive wavelet transform and is based on a model of the active auditory system [11], [12], [13], [14]. The word ‘Bionic’ means that the BWT is directed by an active biological mechanism. The decomposition of BWT is perceptually scaled and adaptive. Properties of BWT includes 1) BWT is a nonlinear transform technique and it has high sensitivity and frequency selectivity. 2) BWT shows a signal with a concentrated energy distribution. 3) The original signal from its time-frequency representation can be reconstructed by inverse BWT. The resolution of BWT in time-frequency domain can be adaptively adjusted not only by the signal frequency but also by the signal’s instantaneous amplitude and its first order differential. This is the most important distinguishing property of BWT.

PROPOSED WORK

This paper proposes Estimated Noise and Adaptive Threshold Bionic Wavelet Transform (ENAT-BWT) speech enhancement technique. This technique is based on Bionic wavelet transform (BWT). A block diagram of the overall approach is shown in Fig. 1.

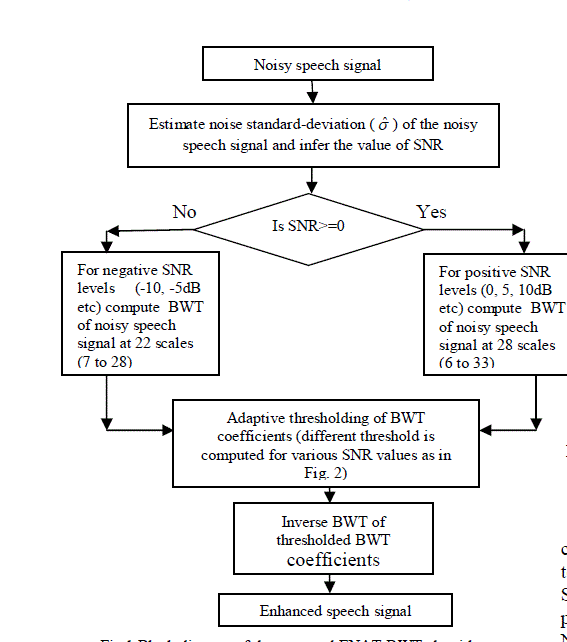Fig.1 Block diagram of the proposed ENAT-BWT algorithm.

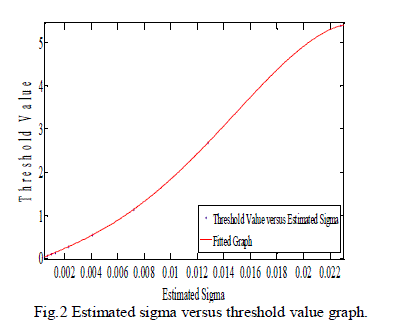
The noise standard-deviation (σˆ ) of the incoming noisy signal is to be calculated first. For this Discrete wavelet transform (DWT) of noisy speech signal is computed using Daubechies wavelet of order 5. Then, standard-deviation (σˆ ) is computed as the median absolute deviation/.6745 of the wavelet coefficients belonging to the diagonal sub band. For negative SNR levels such as -10, -5 dB etc, the bionic wavelet transform (BWT) of the noisy speech signal at 22 scales, from 7 to 28, is taken. At SNR levels of 0, 5 and 10 dB i.e. for positive SNR levels, the bionic wavelet transform (BWT) of noisy speech signal at 28 scales, from 6 to 33, is taken. Initially the thresholds for various noise levels are determined manually that provide the best signal to noise ratios (SNR). Then, using curve fitting approach a generalized model is obtained that provides the best threshold parameter for input noisy signal of any noise standard deviation. The graph obtained after curve fitting is given in Fig. 2. Thus the algorithm selects the threshold value from the graph and soft thresholding is applied to the BWT coefficients. Finally inverse bionic wavelet transform (IBWT) of thresholded BWT coefficients is computed. This provides the enhanced speech signal.

EXPERIMENTAL RESULTS OF THE PROPOSED (ENAT-BWT) ALGORITHM AND COMPARISON WITH OTHER METHODS

A. Criterion of evaluation

For evaluation of the proposed technique, the results are compared to the BWT, PWT and Ephraim Malah filtering techniques. The Signal to Noise Ratio (SNR) and Segmental Signal to Noise Ratio (SSNR) are the performance comparison parameters in this paper. Signal to Noise Ratio is given as

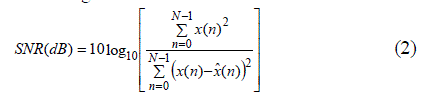where x(n) and xˆ(n) are the original and enhanced speech signals respectively and N is the number of samples in the speech signal.

Segmental Signal to Noise Ratio is given as

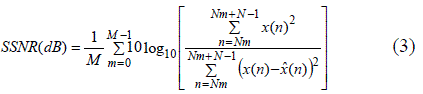where M is the number of frames, N is the size of frame and Nm is the beginning of the m-th frame.

B. Experimental Results

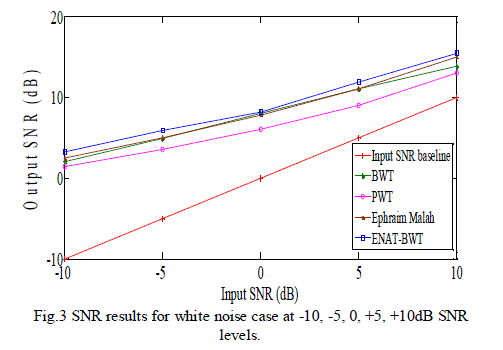
This section presents the experimental results of the proposed algorithm at SNR levels of -10, -5, 0, 5 and 10dB, and compares its performance with the Ephraim Malah filtering, Wavelet Packet Transform (WPT) and the Bionic Wavelet Transform (BWT) algorithm. Five speech signals taken from the TIMIT Acoustic-Phonetic Continuous Speech Corpus [15], were used to evaluate the proposed algorithm. Results are averaged across the 5 utterances used as examples, giving a single evaluation metric for each method. Implementation was done using the Matlab Wavelet toolbox (The MathWorks Inc., 2011). SNR and SSNR results for white noise conditions are shown in Fig. 3 & Fig. 4.

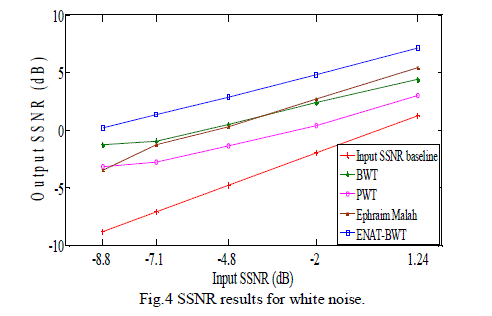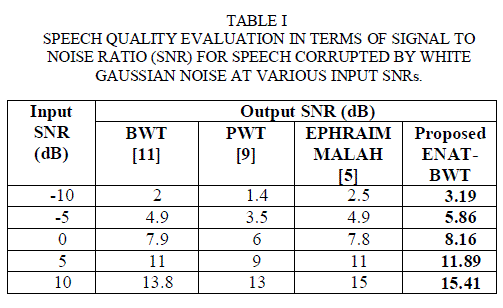
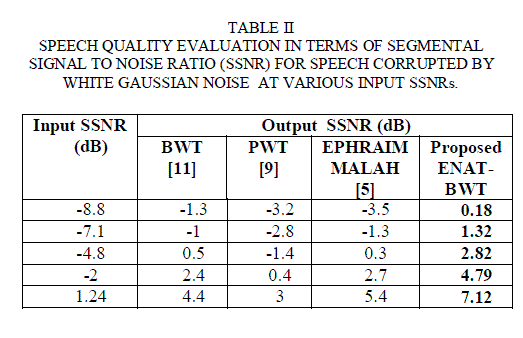
Clearly from these figures, the proposed method shows the best performance for additive white Gaussian noise conditions. The proposed algorithm shows the best SNR improvements at -10, -5, and also at +5 dB noise case as can be seen from Table 1. For SSNR calculation, number of frames taken is 250 and the starting frame’s sample number is 5000. The proposed method shows the best SSNR improvements at -8.8, -7.1, -4.8, -2 and 1.24 dB input SSNR levels. The SSNR results obtained for white Gaussian noise conditions are presented in Table 2.

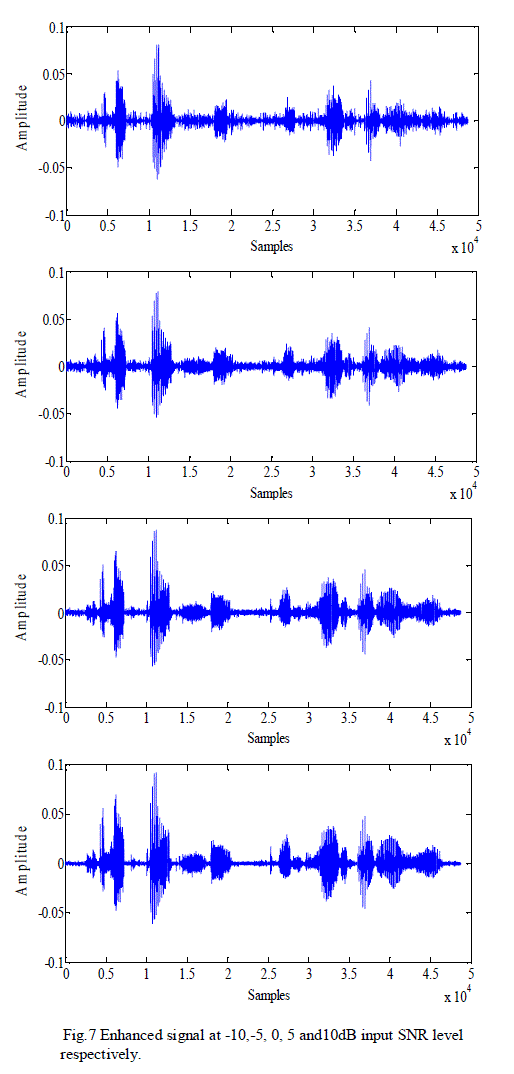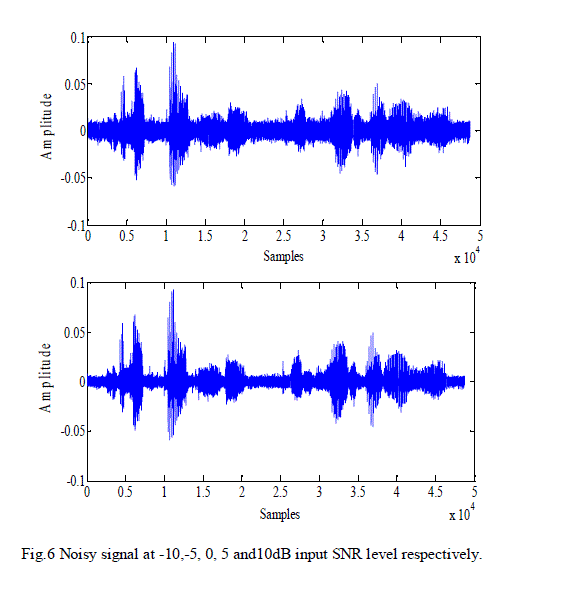
The qualitative performance of the algorithm can be seen from Fig. 5, Fig. 6, and Fig. 7. Fig. 5 shows the original speech signal on which the experiments were conducted.

The noisy signal and enhanced signal at -10, -5, 0, 5 and 10dB input SNR levels are shown in Fig. 6 and Fig. 7 respectively.

CONCLUSIONS

In this paper a new algorithm for speech signal enhancement using the Bionic wavelet transform has been presented. In the proposed Estimated Noise and Adaptive Threshold Bionic Wavelet Transform (ENAT-BWT) algorithm, the number of scales for computation of BWT is different for different SNR inputs. For negative SNR levels the BWT of noisy signal at 22 scales, from 7 to 28, is taken and for positive SNR levels the BWT of noisy signal at 28 scales, from 6 to 33, is taken. Initially the thresholds for various noise levels are determined manually that provide the best signal to noise ratios (SNR). Then, using curve fitting approach a generalized model is obtained that provides the best threshold parameter for input noisy signal of any noise standard deviation. The optimum threshold value is thus automatically selected from the graph and soft thresholding is applied to the BWT coefficients. Finally inverse bionic wavelet transform (IBWT) of thresholded BWT coefficients is computed. This provides the enhanced speech signal. Experimental evaluations were performed on speech signals from the TIMIT database, corrupted by Gaussian noise at various input SNR levels. The performance was evaluated in terms of the Signal to Noise Ratio (SNR) and Segmental Signal to Noise Ratio (SSNR) measures. Denoising results show superior performance of the proposed method as compared to the Bionic Wavelet Transform (BWT), Packet Wavelet Transform (PWT) and Ephraim Malah filtering.

Future work suggests extending the algorithm for higher values of SNR inputs. The algorithm also needs to be tested on other types of noises such as pink noise, babble noise, street noise, railway noise etc.

References

S. F. Boll, “Suppression of acoustic noise in speech using spectral subtraction,” IEEE Trans. Acoustics Speech Signal Processing, vol. 27, no. 2, pp. 113–120, April 1979.

J. R. Deller, J. H. L. Hansen, and J. G. Proakis, Discrete-Time Processing of Speech Signals, 2nd ed., IEEE Press, New York, 2000.

S. Haykin, Adaptive Filter Theory, 3rd ed., Prentice Hall, Upper Saddle River, New Jersey, 1996.

Y. Ephraim, and D. Malah, “Speech enhancement using a minimum mean-square error short-time spectral amplitude estimator,” IEEE Trans. Acoust. Speech Signal Processing, vol. 32, no. 6, pp. 1109 1121, 1984.

Y. Ephraim, and D. Malah, “Speech Enhancement using a minimum mean-square error log-spectral amplitude estimator,” IEEE Trans. Acoust. Speech Signal Processing, vol. 33, no. 2, pp. 443-445, 1985.

R. M. Rao, and A. S. Bopardikar, Wavelet Transforms: Introduction to theory and applications, 6th ed., Pearson Education, 2005.

R. polikar “The wavelet tutorial by RobiPolikar,” Available: http://users.rowan.edu/~polikar/WAVELETS/WTtutorial.html, 1996.

S. H. Chen, S. Y. Chau, and J. F. Want, “Speech enhancement using perceptual wavelet packet decomposition and teager energy operator,” J. VLSI Signal Process. Systems, vol. 36, no. 2–3, pp. 125–139, 2004.

I. Cohen, “Enhancement of speech using bark-scaled wavelet packet decomposition,” paper presented at the Eurospeech, Denmark, 2001.

D. L. Donoho, “Denoising by soft thresholding,” IEEE Trans. Inform. Theory, vol. 41, no. 3, pp. 613–627, 1995.

M. T. Johnson, X. Yuan, and Y. Ren, “Speech signal enhancement through adaptive wavelet thresholding,” Speech Communication, vol. 49, pp. 123-133, 2007.

J. Yao, and Y. T. Zhang, “Bionic wavelet transform: a new time– frequency method based on an auditory model,” IEEE Trans. Biomed.Engineering, vol. 48, no. 8, pp. 856–863, 2001.

X. Yuan, “Auditory Model-based Bionic Wavelet Transform for speech Enhancement,” M. Sc. thesis, Milwaukee, Wisconsin, May 2003.

J. Yao, and Y. T. Zhang, “The application of bionic wavelet transform to speech signal processing in cochlear implants usingneural network simulations,” IEEE Trans. Biomed. Engineering, vol. 49, no. 11, pp. 1299–1309, 2002.

J. Garofolo, L. Lamel, W. Fisher, J. Fiscus, D. Pallett, and N. Dahlgren, et al., TIMIT Acoustic–Phonetic Continuous Speech Corpus: Linguistic Data Consortium, 1993.