ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| V.M. Ramaa Priyaa Asst. Professor, Dept. of E&I, Chennai-600073, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Nanotechnology provides smaller, faster and lower energy devices which allow more powerful and compact circuitry. Memory cells have been protected from soft errors for more than a decade, due to the increase in soft error rate in logic circuits, the encoder and decoder circuitry around the memory blocks have susceptible to soft errors as well and must also be protected. An error occurrence in a computer’s memory system that changes an instruction in a program or a data value. A soft error will not damage a system’s hardware. A new approach is introduced to design fault-secure encoder and decoder circuitry for memory designs. The key contribution is identifying and defining a new class of error-correcting codes whose redundancy makes the design of fault-secure detectors (FSD) particularly simple. Euclidean Geometry codes are also called EG-LDPC codes based on the fact that they are low-density parity-check (LDPC)codes.
Keywords |
| Decoder , Encoder, EG-LDPC codes |
INTRODUCTION |
| Generally nowadays the size of the memory is reduced from microlevel to nanolevel. And the nanotechnology provides powerful and compact circuitry. So as the size decreases the nanomemory is susceptible for soft errors and transient errors. But the storage cells and the communication channels are susceptible to transient errors. Encoders are used to change a signal or data into a code. And the decoders are used to change the code into the signal are data. And this code serves many purposes like compressing information for transmission or storage or encrypting. So there is more possibility of occurring fault in these surrounding circuitries like encoder and decoder. Transient errors are the errors which exist for short period, and the soft errors are the errors which do not have any impact on the hardware. So class of error correcting codes (ECC) is Identified which has appropriate redundancy. Redundancy is the duplication of the critical components of a system which increases the reliability of the system usually in the case of the backup or fail-safe. And it is found that Euclidean Geometry Low-Density parity check (EG-LDPC) codes have the fault secure capability. LDPC codes have a limited number of 1’s in rows and columns of the matrix. So it reduces the complexity and reduces the area. Here EG-LDPC depends upon the structure of the nanomemory. Actually nanomemory architecture consists of nanowire cross wires. And the memory bit is stored at the junction of two cross wires. And the two respective nanowires of that junction are selected by two address decoders, the column address decoder and the row decoder. And adequate voltage is applied at that junction. And thus the memory bit is stored at that junction. And this EG-LDPC depends upon the number of nanowire crossbars and the junction points of the crosswires. And it can detect multiple errors occurring in both the stored codeword in memory and the surrounding circuitries. |
FAULT TOLERANT MEMORY STRUCTURE |
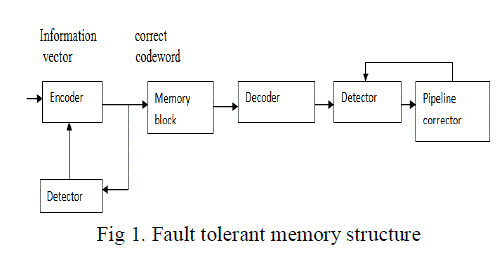 |
| The information bits are fed into the encoder to encode the information vector, and the fault secure detector of the encoder verifies it. If the detector detects any error, the encoding operation must be redone to generate the correct codeword. The codeword is then stored in the memory. During memory access operation, the stored codewords will be accessed from the memory unit. Codewords are susceptible to transient faults while they are stored in the memory therefore a corrector unit is designed to correct errors in the retrieved codewords. Transient errors accumulate in the memory words over time. Inorder to avoid accumulation of too many errors in any memory word, the system must perform memory scrubbing. Memory scrubbing is the process of periodically reading memory words from the memory, correcting the errors and writing them back into the memory. To perform the periodic scrubbing operation, the normal memory access operation is stopped and the memory performs the scrub operation. |
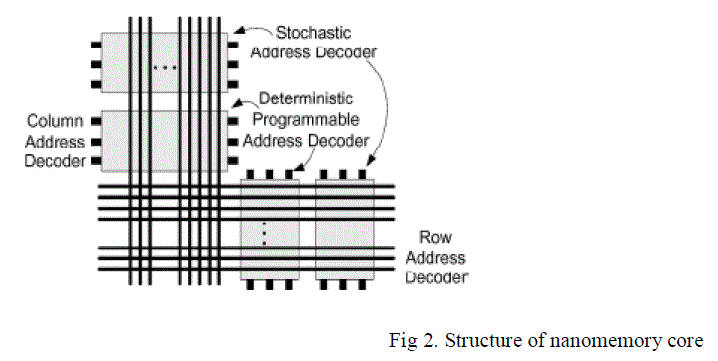 |
| Nano memory are based on nanowire crossbars. Here this nanowire crosswires are used to store the memory bits and a limited number of lithographic scale wires for address wires and defects. The line crossbar stores one memory bit at in each crossbar junction. To be able to write the value of each bit into a junction, the two nanowires crossing the junction must be uniquely selected and an adequate voltage must be applied to them. The nanowires can be uniquely selected through the two address decoders located on the two sides of the memory core. |
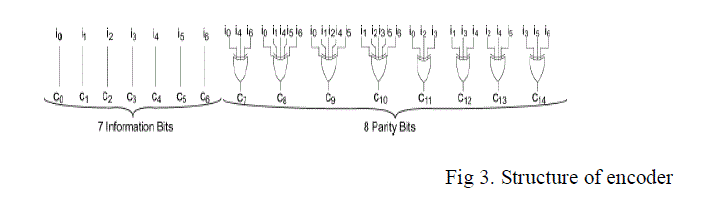 |
| Here the encoded bit is totally 15 bits in which 7 information bits and 8 bits are the parity check bits.c0 to c6 are the information bits,c7 is the xor of i0.i4 and i6, c8 is the xor of i0,i1,i4,i5 and i6,c9 is the xor of i0.i1,i2,i4 and i5, c10 is the xor of i1,i2,i3,i5 and i6, c11 is the xor of i0,i2 and i3, c12 is the xor of i1.i3 and i4, c13 is the xor of i2,i4 and i5, c14 is the xor of i3, i5 and i6. Encoders are used to change a signal or data into a code. And this code serves many purposes like compressing information for transmission or storage or encrypting. And the decoder is used after the memory block and it is used to retrieve the original data or signal from the codes. And these encoder and decoder are more susceptible to the errors like soft errors and transient errors. Soft errors is the error which has only changes in data or information and it doesn’t have any impact on the hardware. |
FAULT SECURE DETECTOR AND CORRECTOR |
| The core of the detector operation is to generate the syndrome vector. |
| 1) (n,k,d) →(15,7,5) where ‘n’ is the coded vector ‘k’ is the input and ‘d’ is the minimum distance. q=n-k =>15- 7=8.First step is to find the generator matrix. G=[Ik : Pk×q ] Where ‘Ik’ is the unit matrix and ‘Pk×q’ is the parity bits. |
| 2) Second step is to find the parity check matrix. H=[PT:Iq]q×n. Where ‘H’ is the parity check matrix, ‘PT’ is the transpose of the parity bits, and ‘Iq’ is the unit matrix. |
| 3) Third step is to find HT |
| 4) Fourth step is to find the syndrome vector. S=CHT. Where ‘C’ is the coded bit that s any row of the generator matrix and ‘HT’ is the transpose of the parity check matrix. And the particular row is xor ed . |
| 5) Fifth step is to detect the errors. If the syndrome matrix contains all ‘0’ s then there s no error. If there s ‘1’ in the syndrome matrix then it indicates the presence of error and it also indicates the place where error is occurred. |
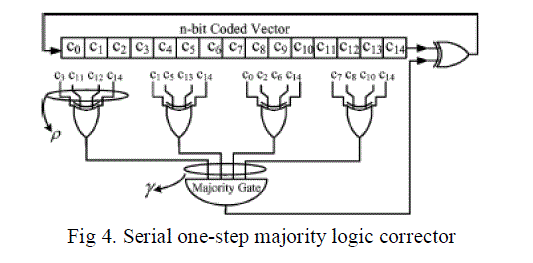 |
| One-step majority logic corrector is a fast and relatively compact error correcting technique. It is the procedure that identifies the correct value of a each bit in the codeword directly from the received codeword. General message passing error correction strategy demand multiple iterations of error diagnosis. So this one-step majority logic corrector makes the correction latency small and deterministic. This technique can be implemented in two ways. Serially to provide compact implementation. Parallely to minimize correction latency. |
| Corrector operation consists of two parts. Generating a specific set of linear sums of the received vector bits. Finding the majority value of the computed linear sums. The majority value indicates the correctness of the code-bit under consideration. If the majority value is 1, the bit is inverted otherwise it is kept unchanged. |
| We use binary sorting networks to do the sort operation. An n input sorting network is the structure that sorts a set of n bits, using 2 bit sorter building blocks. Each of the vertical lines represents one comparator which compares two bits and assigns the larger one to the top output and the smaller one to the bottom. |
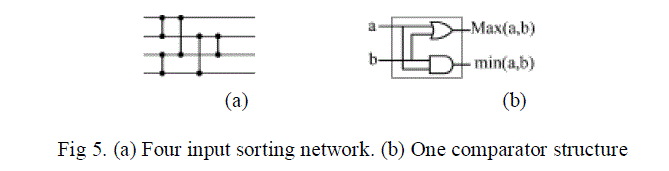 |
| The four input sorting networks, has five comparator blocks consists of two input gates, overall the four input sorting network consists of ten two-input gates in total. In total an eight-input majority gate implemented with sorting networks take 27 two-input gates. In two-level implementation of this majority gate takes 56 five input AND gates and one 56 input OR gate. |
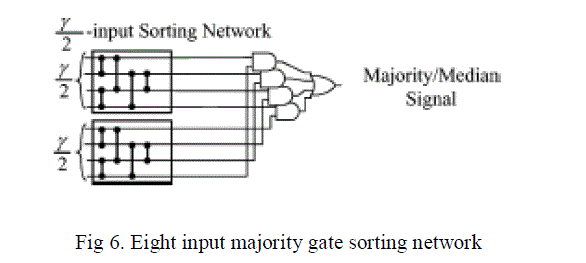 |
CONCLUSION |
| The size of the memory is decreased to nanolevel and the errors like softerrors and transient errors increases and it occurs mostly in the surrounding circuitries like encoder and decoder along with the memory. In this paper a fully fault-tolerant memory system that is capable of tolerating errors not only in the memory bits but also in the supporting logic including the ECC encoder and corrector. Here Euclidean Geometry codes are used. And it is proved that these codes are part of new subset of ECCs that has FSDs. Using these FSDs we have designed a fault-tolerant encoder and corrector, where the faultsecure detector monitors their operation. And a unified approach is presented to tolerate permanent defects and transient faults. And this unified approach reduces the area overhead. |
References |
|