1Faculty of Science and Technology, Universiti Sains Islam Malaysia (USIM), Malaysia
2Department of Mathematics, Faculty of Science, Universiti Putra Malaysia, Malaysia
3Institute for Mathematical Research, Universiti Putra Malaysia, Malaysia
4Malaysia-Japan International Institute of Technology, Universiti Teknologi Malaysia (UTM), KL, Malaysia
Received date: 10/03/2016; Accepted date: 14/04/2016; Published date: 18/04/2016
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In this note, convex Homotopy perturbation method (HPM) is presented for the approximate solution of the linear Fredholm-Volterra integral and integro-differential equation. Convergence and rate of convergence of the HPM are proved for both equations. Five numerical examples are provided to verify the validity and accuracy of the proposed method. Example reveals that HPM is very accurate and simple to implement for integral and integrodifferential equations.
Approximate method, Homotopy perturbation method, Convergence, Error estimate
Integral equations occur naturally in many fields of science and engineering [1]. A computational approach to solve integral equation is an essential work in scientific research. Fredholm and Volterra integral equation is one of the most important integral equations.
Some iterative methods like Homotopy perturbation method (HPM) [2-11] and Adomian decomposition method (ADM) [12-14], Homotopy analysis method [15-22] have been applied to solve linear and nonlinear Fredholm and Volterra integral equations and integro-differential equations.
HPM has been used for a wide range of problems; for finding the exact and approximate solutions of nonlinear ordinary differential equations(ODEs) [7], linear and nonlinear integral equations [8], the integro-differential equations [9,10] and the Volterra- Fredholm integral equations [11]. Hetmaniok et al. [23] have proposed method which is based on the homotopy perturbation method to solve Volterra–Fredholm integral equations of the second kind. The problem of the convergence of the series constructed is formulated and a proof of the formulation is given. Additionally, the estimation of the approximate solution is elaborated by taking the partial sums of the series. In 2016, Zulkarnain et al. [24] consider Fredholm-Volterro integro-differential equation (FVIDE) of order of the third kind and solved it by using modified homotopy perturbation method (HPM). It is found that MHPM is a semianalytical method and easy to apply for FVIDE. Numerical examples are given to present the efficiency and reliability of the method.In this note, we consider two types of integral equations:
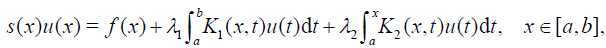 (1)
(1)
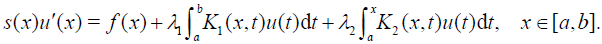 (2)
(2)
Eqs. (1)-(2) are called Fredholm-Volterra integral equations (FVIEs) and Fredholm-Volterra integro-differential equations (FVIDEs) of the third kind respectively. For both type of equations the convergence of approximate solutions are established and four examples are provided to verify the accuracy of the proposed method.
The paper is organized as follows. In Section 2, we present the application of the HPM for the problem (1) and proof of the convergence. In Section 3, HPM is modified to solve the Eq. (2) and present the rate of convergence of the approximate solution. Section 4 provides four examples: first two examples related to the Eq. (1) and another two more examples dealt with Eq. (2). Numerical results show that the proposed methods are very accurate and converge fast. Conclusion is given in Section 5.
To explain the homotopy perturbation method (HPM), we consider the general integral equation of the form
Lu + Nu = f (3)
where L ia a linear operator and N is nonlinear operator.
As a possible remedy, we can define homotopy H(v, p) by
H(v, p) = (1− p)F(v) + p(L(v) + N(v) − f ) (4)
where F(v) is a functional operator with known solution u0 , which can be obtained easily. It is clear that, for
H(v, p) = 0 (5)
from which we have
H(v,0) = F(v). H(v,1) = Lv + Nv − f (6)
This shows that H(u, p) continuously traces an implicitly defined curve from a starting point H(v0,0) to a solution H(u,1) . The embedding parameter p monotonically increases from zero to unit as the trivial problem F(v) = 0 is continuously deformed to the original problem L(u) + N(u) − f = 0 . The embedding parameter p∈(0,1] can be considered as an expanding parameter [2].
To obtain the approximate solution of Eq.(3) we search solution in the series form
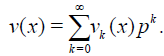 (7)
(7)
When p →1 , Eq.(5) corresponds to Eq. (3) and becomes the approximate solution i.e.,
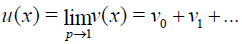 (8)
(8)
The series (8) is convergent for most cases, and the rate of convergence depends on L(u) and N(u) .
Let us consider the linear Fredholm-Volterra integral equation (1) where the kernels K1 ,K2 ∈C([a,b]×[a,b]) and the functions s, f ∈C[a,b] are known, whereas the function is to be determined. Define the operators L(u) and N(u) for Eq. (1) as follows
Lv(x) = s(x)v(x)
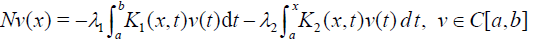
with the assumption that s(x) ≠ 0 for any x∈[a,b] . Rewriting Eq. (4) in the form
H(v, p) = Lv - u0 + p(u0+ Nv - f ) (9)
we solve the problem (1) as follows. For p = 0 the solution of the operator equation H(v,0) = 0 is equivalent to the solution of a trivial problem s(x)v(x) - u0(x) = 0 . For p = 1 the equation H(v,1) = 0 leads to the solution of Eq. (1).
By substituting the series solution (7) into the Eq. (5) and according to Abel’’s Theorem the solution of Eq. (1) is obtained from the equation
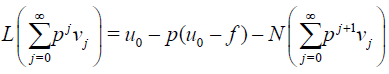
Comparing the same power of parameter p in both sides of Eq. (10), leads to the following relations
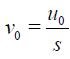 (11)
(11)
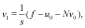 (12)
(12)
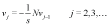 (13)
(13)
According to the scheme (11)-(13) we define partial sum as follow
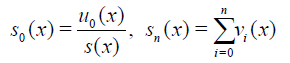 (14)
(14)
Theorem 1 thm1 Let K1 ,K2∈C([a,b]×[a,b]) and s, f ∈C[a,b] where s(x) ≠ 0 for any x∈[a,b] , be continuous functions. In addition, if the following inequality
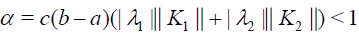 (15)
(15)
Where 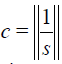 is satisfied and initial guess u0 is chosen as a function continuous on the interval [a,b] , then series solution (7) is uniformly convergent to the exact solution u on the interval [a,b] for each p = [0,1] .
is satisfied and initial guess u0 is chosen as a function continuous on the interval [a,b] , then series solution (7) is uniformly convergent to the exact solution u on the interval [a,b] for each p = [0,1] .
Proof. Prove of the Theorem 1 has not much changes of the Hetmaniok et al [23]. [Theorem 1].
Remark 1 Hetmaniok et al. [23] [Remark 1]. In the thm1, the interval [a,b] can be replaced by (a,b),(a,b] or [a,b) , whereas the condition of continuity of Ki for i = {1, 2} and f in the appropriate regions 1 Ω and 2 Ω must be strengthened by adding the assumption of boundedness of these functions. Moreover, the conditions Ki∈([a,b]*[a,b]]) can be replaced by some weaker condition, for example by the Lebesque integrability of kernel Ki on the set [a,b]×[a,b] and by the inequality [25]
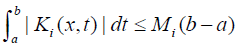
In the case of difficulties or impossibility of finding the sum of series (7) for p = 1, we may consider an approximate solution by taking the partial sum of the series (14). The first n +1 terms of series (14) in the limit p →1 create the so-called n th-order approximate solution in the form
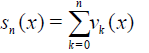 (16)
(16)
The solution sn(x) in (16) can be estimated on the basis of the following theorem. Theorem 2 is not much difference given in Hetmaniok et al. [23] [Theorem 2]
Theorem 2 The error of nth-order approximate solution of (16) can be estimated by the inequality
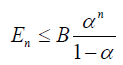
where 
Proof.
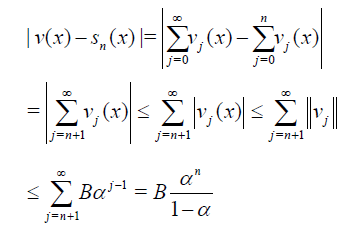
Let us introduce the space of continuously differentiable functions C1([a,b]) equipped with the norm
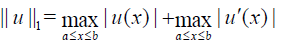 (17)
(17)
i.e,
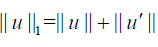
where 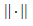 is the standard norm in C[a,b] .
is the standard norm in C[a,b] .
To apply convex HPM for FVIDEs (2) we rewrite it in the form
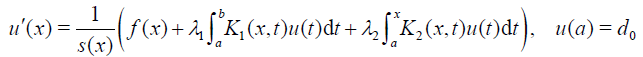 (18)
(18)
where u′(x) is the first order derivative of u(x) with initial condition u(a) = d0 and integrate both sides of Eq. (??) to yield
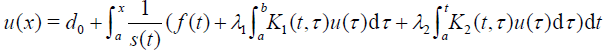 (19)
(19)
Write Eq. (19) in operator form
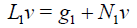 (20)
(20)
where
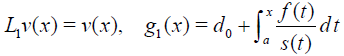
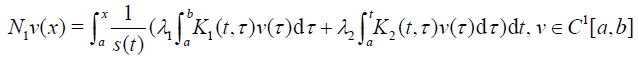 (21)
(21)
Using the above definitions we obtain the homotopy operator for Eq.(??) as
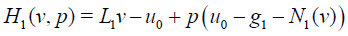 (22)
(22)
where p∈[0,1] is homotopy parameter and u0(x) defines as initial guess for Eq.(??). In a similar way, substituting the series solution (7) into equation
H (v, p) = 0
leads
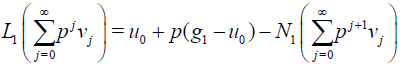 (23)
(23)
Comparing the expressions with the same power of parameter p , we obtain
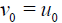 (24)
(24)
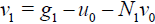 (25)
(25)
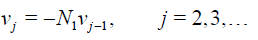 (26)
(26)
Next, for the derivative of v we define
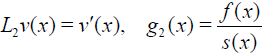
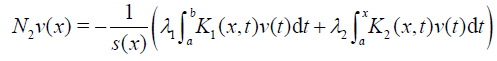 (27)
(27)
By using the homotopy perturbation method, the solution of operator equation
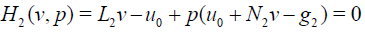 (28)
(28)
is searched in the form of power series
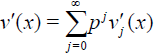 (29)
(29)
If the series (29) possesses a radius of convergence not greater than 1, then the series is absolutely convergent. By putting (29) into the Eq. (28) and comparing the expressions with the same power of parameter p leads to the relations
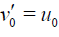 (30)
(30)
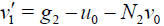 (31)
(31)
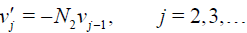 (32)
(32)
The convergence of the approximate solution (7) of Eq. (2) is given in the Theorem 3..
Theorem 3 Let 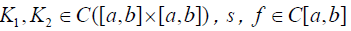 be continuous function on the respective domain. In addition, if the inequality
be continuous function on the respective domain. In addition, if the inequality
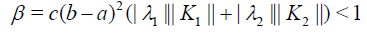 (33)
(33)
where 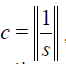 holds and the initial value u0 is chosen as continuous function, then the series in Eqs. (7) is uniformly convergent to the exact solutions u(x) in the sense of the C1 norm on the interval [a,b] for each p∈[0,1] .
holds and the initial value u0 is chosen as continuous function, then the series in Eqs. (7) is uniformly convergent to the exact solutions u(x) in the sense of the C1 norm on the interval [a,b] for each p∈[0,1] .
Proof. Since the kernels K1,K2 and the function f (x) , s(x) with s(x) ≠ 0 , x∈[a,b], are continuous in the respective closed domain then
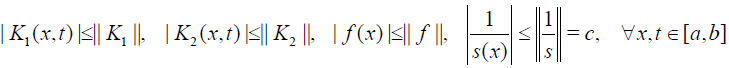
Let u0 be chosen as continuous function and
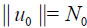
Then from the relations (24)-(26) it follows that
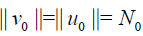
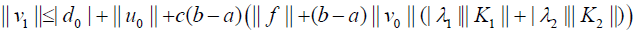
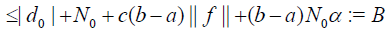
For the general case, from (26) we have the following estimation:
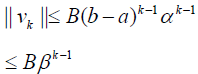 (34)
(34)
where β = (b − a)α
From the series (7), for p∈[0,1] it follows that
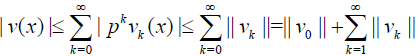
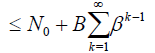
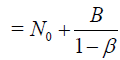 (35)
(35)
Since the the estimate series (??) is the geometric series with the common ratio β and therefore it is convergent if common ratio β < 1 . It implies that v(x) is uniformly convergent on [a,b] for each p∈[0,1] .
The assumptions for relations (30)-(32) implies
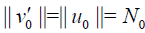
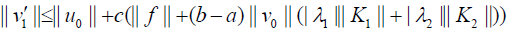
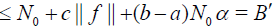
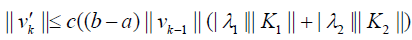
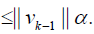
Substituting (??) into the estimation of v′k(x) yields:
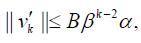
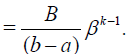
For the series in (29), we get
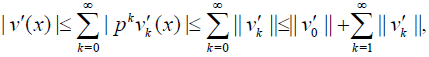
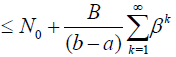
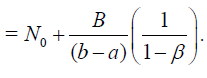 (36)
(36)
The series
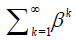 is the convergent geometric series possessing the common ratio β < 1 . Hence, the solution v(x) is differentiable. So that both series (7) and (29) are convergent if | β |< 1 . Then according (17) we obtain convergence of the series (7) to the exact solutions u(x) in the sense of the C1 norm.
is the convergent geometric series possessing the common ratio β < 1 . Hence, the solution v(x) is differentiable. So that both series (7) and (29) are convergent if | β |< 1 . Then according (17) we obtain convergence of the series (7) to the exact solutions u(x) in the sense of the C1 norm.
The partial sum sn(x) in Eq. (16) and its derivative can be estimated as follows.
Theorem 4 The error n E of nth-order approximate solution of (19) and its error of n th-order approximate derivative En' defined by (18) can be estimated by
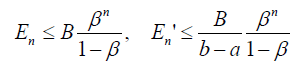
Where 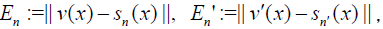 while
while 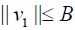 and
and 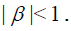
Proof
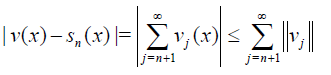
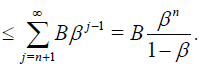
and
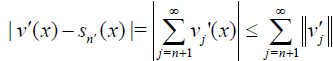
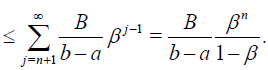
Let the error estimate En and relative errors δn be defined by
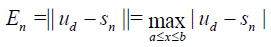
and
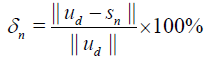
Example 1 Consider the Fredholm-Volterra linear integral equation
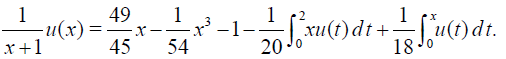 (37)
(37)
Hence
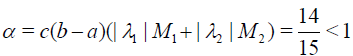
conditions of Theorem 1 holds, therefore HPM is convergent for any choice of initial guess. Let us choose 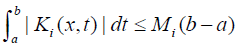 then calculating the successive functions vj determined by relations (11)-(13) we obtain
then calculating the successive functions vj determined by relations (11)-(13) we obtain
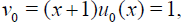
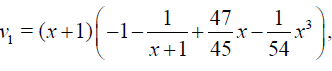
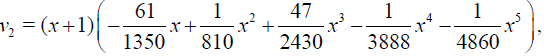
Table 1 shows that the errors decreases very fast when number of terms n increases.
| n | 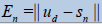 |
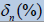 |
n | 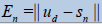 |
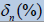 |
|---|---|---|---|---|---|
| 5 | 4.17343915*10-6 | 1.39114638*10-5 | 20 | 7.30756701*10-19 | 2.43585567*10-17 |
| 10 | 2.35172667*10-10 | 7.83908886*10-9 | 25 | 4.07349003*10-23 | 1.35783001*10-21 |
| 15 | 1.31092835*10-14 | 4.36976116*10-13 | 30 | 2.27070391*10-27 | 7.56901305*10-26 |
Table 1: Errors of the approximate solutions sn (x) defined by (16) for Eq. (37).
Example 2 Consider the Fredholm-Volterra integral equation
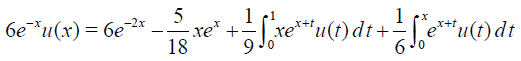 (38)
(38)
with the exact solution ud(x)=e-x .
Solution. Let initial guess u0 = 0 be given. From Eq. (38) it follows that
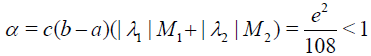
Parameter α in Eq. (38) satisfies the inequality (15).
From the Table 2 it can be seen that the absolute and relative errors are decreased very fast when number of terms n increases.
| n | 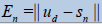 |
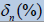 |
n | 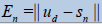 |
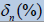 |
|---|---|---|---|---|---|
| 5 | 8.52615826*10-8 | 8.526158263*10-6 | 20 | 5.59658360*10-30 | 5.59658360*10-28 |
| 10 | 3.43859915*10-15 | 3.43859915*10-13 | 25 | 2.25784296*10-37 | 2.25784296*10-35 |
| 15 | 1.38724210*10-12 | 1.38724209*10-20 | 30 | 9.108865591*10-45 | 9.10886559*10-43 |
Table 2: Errors of the approximate solutions sn(x)defined by for Eq. (38).
Example 3 Consider the Fredholm-Volterra integro-differential equation of third kind
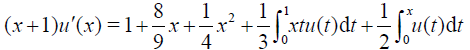 (39)
(39)
with the exact solution ud=x and initial condition u(0) = 0 .
Solution. From Eq. (39) we have
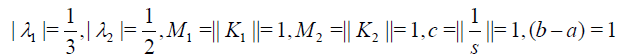
Hence,
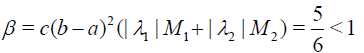
satisfies the conditions of Theorem 3. By choosing the initial function u0(x) =1 we obtain (Table 3):
| n | 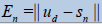 |
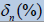 |
n | 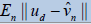 |
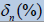 |
|---|---|---|---|---|---|
| 5 | 1.96687746*10-9 | 1.96687746*10-7 | 20 | 7.97754087*10-36 | 7.97754087*10-34 |
| 10 | 4.75088504*10-18 | 4.75088504*10-16 | 25 | 3.82804414*10-45 | 3.82804414*10-43 |
| 15 | 1.02017261*10-26 | 1.02017261*10-24 | 30 | 1.81398763*10-53 | 1.81398763*10-51 |
Table 3: Errors of the approximation solutions (16) for Eq. (39)
From these results we can conclude that the approximate solution converges very fast to the exact solution when n increases.
Example 4 Consider the Fredholm-Volterra integro-differential equation of third kind
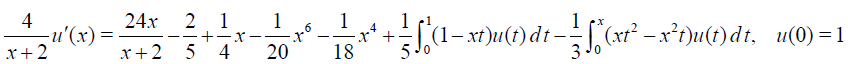 (40)
(40)
Solution. Exact solution of Eq. (40) is ud=1+ 3x2. It is not difficult to see that
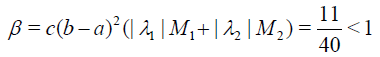
satisfies the condition of Theorem 3.
The results in Table 4, show that the absolute and relative errors of Eq. (40) decreases very fast with initial guess u0(x)=x+2 .
| n |  |
 |
n | 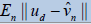 |
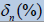 |
|---|---|---|---|---|---|
| 5 | 5.79771528*10-7 | 1.44942882 *10-5 | 20 | 4.38679146*10-27 | 1.09669786*10-25 |
| 10 | 1.13820421*10-13 | 2.84551053*10-12 | 25 | 8.61212628*10-34 | 2.15303157*10-32 |
| 15 | 2.23451662 *10-20 | 5.58629154*10-19 | 30 | 1.69072818*10-40 | 4.22682043*10-39 |
Table 4: Errors of the approximation solutions (16) for Eq. (40)
Example 5 Consider the Fredholm-Volterra integral equation of the third kind in the form
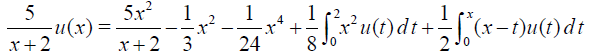
Solution. The exact solution is u(x)= x2 with the initial guess 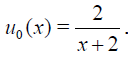 .In this example, the conditions of the Theorem 2 fails. Since
.In this example, the conditions of the Theorem 2 fails. Since
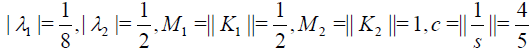
hence
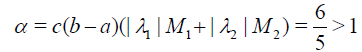
From the Table 5, we can conclude that approximate solution for Eq. (41) would converges to the exact solution but it might depends on the choice of the initial guess.
| n | 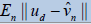 |
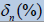 |
n | 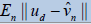 |
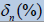 |
|---|---|---|---|---|---|
| 5 | 6.01228713*10-3 | 0.15030718 | 20 | 5.09091226*10-11 | 1.27272807*10-9 |
| 10 | 1.22543958*10-5 | 3.06359894*10-4 | 25 | 1.03764182*10-13 | 2.59410456*10-12 |
| 15 | 2.49772003*10-8 | 6.24430008*10-7 | 30 | 2.11494619*10-16 | 5.28736548*10-15 |
Table 5: Errors of the approximation solutions (16) for Eq. (41)
In this note, we have analyzed HPM for solving linear FVIEs and FVIDEs of the third kind. From the Theorem 2 it follows that HPM for FVIEs converges uniformly if α < 1 . Meanwhile, HPM for FVIDE is uniformly convergent and differentiable if β < 1 .
Examples 1-2 corresponding Tables 1 and 2 verify that HPM is very accurate and stable for the FVIEs. Meanwhile Examples 3-4 show that HPM is convergent to the exact solution very fast when number of points n increases. Example 5, shows that convex HPM converges to the exact solution by the suitable choice of initial guess even though conditions of Theorem 2 is not satisfied.
From the examples above, we can conclude that HPM method for solving FVIE and FVIDE converge very fast when number of point n increases and given functions and kernels are satisfied the certain conditions in thm1 and thm3.
This work was supported by University Putra Malaysia under Fundamental Research Grant Scheme (FRGS, 2011). Project code is 01-12-10-989FR.