ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| Poovizhi Panpa P PG Student, Easwari Engineering College, Chennai, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Critical properties of software systems, such as reliability and performance, should be examined early in the development, when they can govern important architectural design decisions. Several architecture-based reliability analysis methods have been developed to support this task. However, these methods either oversee individual impact factors on reliability or hard-code them into formal models, which strongly limits their applicability to support architectural design in component-based development processes. Our approach, based on the Palladio Component Model (PCM), considers the relevant architectural factors of software systems in a highly parameterized UML-like model, allowing for transparent evaluation of architectural design options. It models the propagation of the system usage profile and execution environment throughout the architecture and automatically derives the component usage profiles, which are overseen in most of the existing approaches. Before analysis, the model is automatically transformed into a formal analytical model. Using a realistic example, we demonstrate the support of usage profile analysis.
Keywords |
| Component-Based Software Engineering, Discrete Time Markov Chain, Palladio Component Model (PCM), Parameter Dependencies, Service Effect Specifications (SEFF), Usage Profile |
INTRODUCTION |
| Software systems are increasingly being used in diverse fields and handle many time and mission critical jobs to support business and industrial processes. Formal techniques to analyse the properties of software systems are useful not only for functional properties, but also for extra-functional properties, such as reliability, performance, security, etc. Reliability can be informally defined as the fraction of time that a system operates correctly. More formally, it is defined as the probability of failure-free operation of a software system for a specified period of time in a specified environment [1]. Predicting the reliability of a system can help avoid implementing component-based software architectures that do not fulfil user requirements, thereby substantially saving costs for fixing an implementation based on a poor architecture. Architecture-based reliability prediction can be used to evaluate the quality of the system design and also to recognize reliability-critical elements of the architecture. This supports fundamental design decisions early in the development process. |
| For architecture-based software reliability analyses, one requires reliability specifications of individual software components. These values are ideally provided by the component vendors. However, it is hard for a vendor to provide the reliability of a software component, because the value not only depends on the component’s implementation, but also on some other factors that are outside the control of the vendor, such as its usage profile, the reliability of the external services and the reliability of the execution environment. |
| Many of the existing approaches (e.g., [2], [3]) do not explicitly model the influence of the system usage profile on the control and data flow throughout the architecture. They encode a system usage profile into formal models implicitly in terms of transition probabilities in the Markov models. Since the models are bound firmly to a specific usage profile, repetition of much of the modeling effort is required to evaluate reliability for a different usage profile. Furthermore, many approaches do not consider the impact of the execution environment on the system’s reliability. Even though the software is completely fault-free, failures may occur due to unavailable hardware resources and failed communication network links across components. Ignorance of these factors leads to overoptimistic reliability prediction (e.g., [2], [3]). On the contrary, approaches (e.g., [4]) considering the execution environment offer no means to model applicationlevel software failures, also resulting in a limited view of software system reliability. |
| This paper strives to remedy the shortcomings of previous approaches with an innovative technique for architecturebased software reliability modeling and prediction that explicitly examines and integrates the reliability-relevant factors mentioned above. The technique propagates the usage profile throughout a component-based software architecture by resolving parameter dependencies and accounts for execution environment by evaluating service execution under different hardware availability states. The Palladio Component Model (PCM) [8] is used as a design-oriented modeling language for component-based software architectures by extending the PCM with capabilities for reliability prediction. Tool support for automated transformation of PCMs into Markov chains and space-effective evaluation of these chains is provided. |
| Multiple developer roles are supported by the PCM as they can independently contribute their parts to the architectural model. This reduces the complexity of the overall task. The whole approach is implemented as an Eclipse-based tool [7] that not only supports the modeling process and reliability analysis, but also the reliability simulation and sensitivity analysis, further facilitating the architectural design. The rest of the paper is organized as follows: Section 2 discusses the related work. Section 3 briefs the most important concepts of the PCM. Section 4 details on the reliability prediction of a PCM instance. Section 5 concludes our work. |
RELATED WORK |
| Seminal work in the area of software reliability engineering [1] focuses on system tests and reliability growth models treating systems as black boxes. Lately, many architecture-based reliability analysis approaches have been proposed, treating system as a composition of software components. Subsequently, these approaches regarding their modeling of the influence factors on component reliability are examined. |
| System usage profile can be described in terms of the expected sequence of system calls (including their probability) and the input parameters values used for these calls, which may influence the entire system control flow. To model the influence of the usage profile on system reliability, the propagation of inputs from the user to the components and from components to other components (external calls) has to be modelled. Goseva et al. [3] state that most approaches rely on estimations of transition probabilities between components. Cheung [2] mentions that transition probabilities could be obtained by assembling and deploying the components and executing the expected usage profile against them. However, this requires the software architects to set up the entire system during the architectural design, which is often neither desired nor possible. |
| Contemporary approaches by Wang et al. [9] and Sharma et al. [10] extend Cheung’s work to support various architectural styles and combined performance and reliability analysis. However, they confide on testing data or the software architect’s insight to compute the transition probabilities. The work of Reussner et al. [11] assumes fixed transition probabilities between components; therefore its models cannot be reused if the system-level usage profile varies. Cheung et al. [6] focus on the reliability of individual components and do not include calls to other components. |
| Numerous approaches incorporating properties of the execution environment into software reliability models have been proposed. Sharma et al. [4] provide a software performability model that includes hardware availability and different states of hardware resources, but disregard the usage profile propagation and component dependencies. Besides, the approach computes the throughput of successful requests in presence of hardware failures, but not the system reliability. The same holds for the approaches of Trivedi et al. [13] and Vilkomir et al. [14] who designed complex availability models of the execution environment, however, did not associate it to the software level to estimate the overall system reliability. |
| Popic et al. [15] take failure probabilities of network connections into account, but not the failure probabilities of other hardware resources. Sato and Trivedi [16] integrate a system model of communication system services to a resource availability model. Nevertheless, they do not include pure software failures (that are not activated by execution environment), assume fixed transition probabilities among services, and do not model usage profile dependencies of services. Yacoub et al. [17] include communication link reliabilities in their approach but neglect hardware availability. |
 |
| In general, there is a need for an integrated modeling and evaluation approach that allows the system reliability prediction of component based software systems with varied usage profiles and execution environments. This is the focus of this paper. We describe the details of our modeling and evaluation approach in the ensuing sections. |
MODELING RELIABILITY WITH THE PCM |
| To give a brief prologue to the reader about the modeling capabilities of the PCM, we begin with the discussion of a simple example (Section A), followed by a more elaborate narration of the modeling capabilities structured according to the involved developed roles (Section B) and finally an introduction to the PCM extensions regarding reliability modeling (Section C). |
| A. Example |
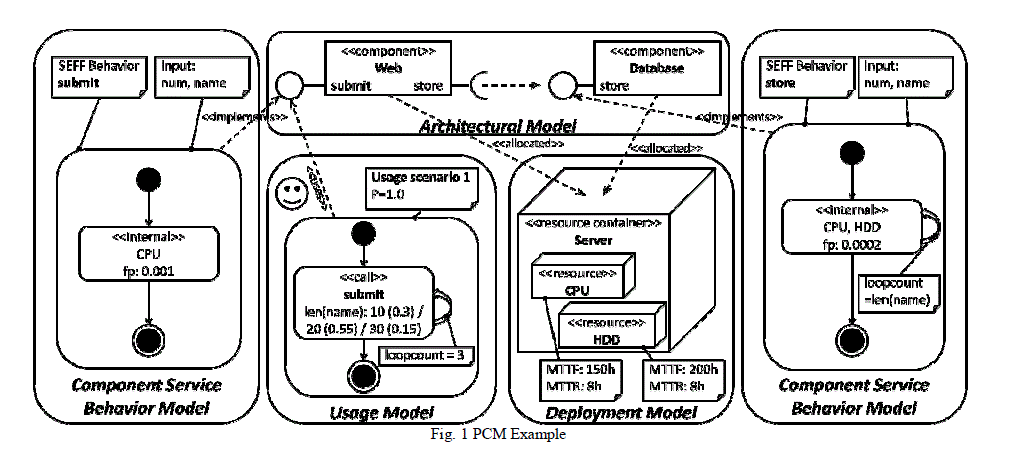
| Fig. 1 shows an example of a PCM instance that models a simple web server system. It allows for a submit operation which stores, in the database, the number and the name passed to it. |
| The PCM is composed out of four kinds of models delivered independently by four different developer roles. The roles may contribute their parts independently from other roles, supporting a distributed component-based development process through equally distributed modeling contributions. The roles realized by the PCM are the component developer, software architect, system deployer, and domain expert. |
| Component developers provide abstract behavioural specifications of component services resulting in component service behaviour models. They can annotate internal computations of a service with failure probabilities. Furthermore, they can annotate external calls as well as control flow constructs with parameter dependencies. The latter allow the model to be adjusted for different system-level usage profiles. Software architects retrieve the component specifications from a repository and compose them into an architectural model by specification of a component wiring. They do not deal with component internals, but instead fully rely on the SEFFs supplied by the component developers. System deployers define a resource environment annotated with failure properties and allocate the components in the architectural model to the resources, building the deployment model of the system. Finally, domain experts specify the system-level usage model in terms of stochastic call sequences and input parameter values, which then can be automatically propagated through the entire model. Once the whole model is specified, it can be transformed into a Markov model to conduct reliability predictions |
| B. PCM Architectural Modeling Capabilities |
| This section provides a more elaborate explanation of the individual PCMs. For a complete summary, including the metamodel, refer to [8]. |
| 1) Component Service Behaviour Models: This part of the PCM comprises behavioural specifications of component provided services, together with their input parameters and associated component parameters. The example in Fig. 1 consists of two SEFF models, each modeling a single provided service of a component used in the architectural model. The submit service is the provided service of the Web component. The submit SEFF specifies the high-level control and data flow as follows: After execution start, the internal action (stereotype << internal >>) represents the submit operation, using a CPU resource type. There is another stereotype << call >> that can be used to represent an external call action to another service of another component. The other SEFF store is the provided service of the Database component. It also consists of only one internal action, however, the service executes a more complex search (using CPU and HD resource types) iteratively, with the number of iterations influenced by the length (or bytesize) of the name parameter. |
| 2) Architectural Model: The components—as specified through their respective component service behavior models—are connected by a software architect into an architectural model of the system. Additionally, software architects define the system boundaries and determine the provided interfaces that shall be exposed to system users or other systems. In Fig. 1, the architectural model connects the Web and Database components through the required and provided store service, with the submit service being exposed to external system users. |
| 3) Deployment Model: The deployment model models the resource environment, which is a set of resource containers (i.e., computing nodes) connected via network links. Each resource container may include a number of modelled hardware resources (e.g., CPU, hard disk, memory, etc.). Resources have attributes, such as failures rates or scheduling policies. System deployers specify concrete resources, while component SEFFs only refer to abstract resource types. When specifying the allocation of components to resource containers, the resource demands can be directed to concrete resources. This method allows easy exchanging of the resource environment in the model without the need to adapt the component specifications. The resource environment of Fig. 1 consists of one resource container Server. The resource containers provide CPU and HDD (hard disk drive) resources that may be used by the submit and store components, corresponding to the specified component allocation. |
| 4) Usage Model: The usage model is provided by domain experts and it captures the system’s usage profile. It consists of a set of usage scenarios representing different user classes or use cases of the system. Each scenario contains sequences of system service calls, including probabilistic control flow constructs to express existing variabilities within each use case or user class. If a service signature contains input parameters, the domain experts may characterize their values and other properties. They can use the stochastic expression language to model parameter properties with arbitrary probability distributions. Fig. 1 contains a simple usage model, consisting of a single usage scenario. Each system user arrives at the system, enters a series of three invocations of the submit service, and leaves the system. Each call to submit has the same probability distribution for the input parameter name’s length i.e. len(name): 10, 20, or 30. |
| Our approach can be used to support the evaluation of single usage scenarios in isolation and also multiple parallel usage scenarios. In the second case, a probability for the stimulation of all the individual usage scenarios must be indicated. The reliability analysis then determines the overall system reliability weighted by the usage scenario probabilities. |
| C. PCM Extensions for Modeling Reliability |
| In this section, we describe the new reliability-relevant concepts incorporated into the PCM metamodel originally designed for performance modeling and prediction. |
| Software failures occur during a service execution due to faults in the implementation. A PCM internal action in a SEFF abstracts component-internal processing and can be annotated with a failure probability that depicts the probability that the internal action fails during execution. It is deemed that any failure of an internal action causes a system failure. Component developers can use statistical testing, software reliability growth models or code coverage metrics on their components to estimate their respective failure probabilities. |
 |
| Communication link failures include loss or damage of messages during transport, resulting in a service failure. Although transport protocols like TCP accommodate mechanisms for fault tolerance, failures can still take place as a result of overload, physical damage of the link, or other reasons. As such failures are largely unpredictable from the viewpoint of the system deployer, they are looked upon like software failures and the communication links are annotated with a failure probability in the PCM model. These failure probabilities can either be defined from experience with similar systems or by running tests on the target network. |
| Unavailable hardware causes a service execution to fail. Hardware resource breakdowns primarily occur due to wear outs. Ultimately, a broken-down resource is quite often repaired or replaced by a functionally analogous new resource. In the PCM, hardware resources are annotated with their Mean Time To Failure (MTTF) and Mean Time To Repair (MTTR) specified by the system deployers. Hardware vendors often provide MTTF values in specification documents. System deployers can refine these values on experience. |
PREDICTING RELIABILITY WITH THE PCM |
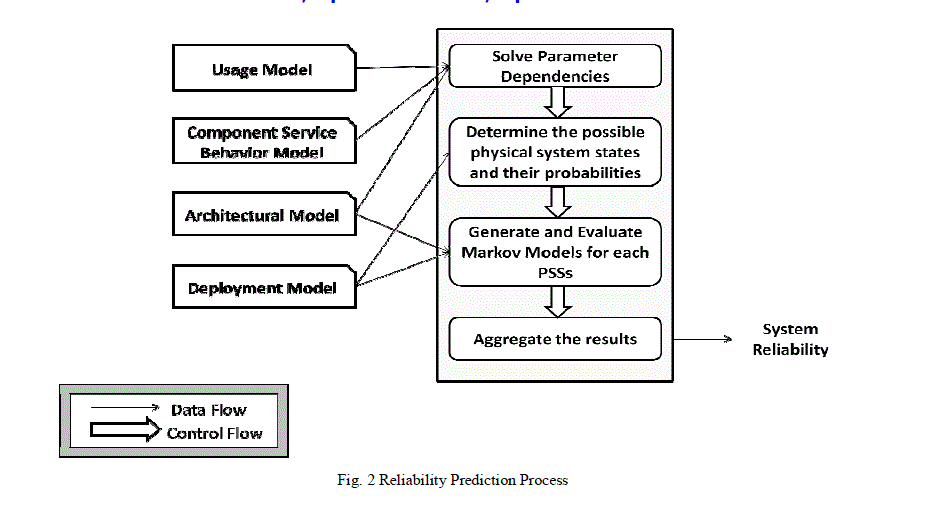
| The prediction process is depicted in the Fig. 2, together with the preceding modeling and subsequent design assessment steps. |
| A. Solving Paramater Dependencies |
| Component developers specify the high-level behavior of their components through service effect specifications. These SEFFs may contain parameter dependencies to express the influence of input parameter values on the control and data flow. To resolve all parameter dependencies throughout a PCM instance, the existing PCM Dependency Solver is reused. Starting from the given usage scenario, the Dependency Solver traverses the specified SEFFs recursively and resolves all parameter dependencies on its way. Each resolving step includes parsing and resolving a stochastic expression with arbitrary probability distributions, references to input parameters with different data types, and different kinds of operators. |
| B. Determining Probabilities of Physical System States |
| A physical system state is composed of all individual states of the system’s hardware resources, which are defined in the PCM resource environment and allocated to resource containers. Let R = {r1, r2, . . . , rn} be the set of resources in the system. Each resource ri is characterized by its MTTFi and MTTRi, with two possible states OK and NA (not available). Within our approach, we do not use the specified MTTFi and MTTRi values directly for reliability prediction. Instead, we calculate the steady-state availability Av of resource ri: |
 |
| C. Generating and Evaluating the Markov Model |
| Based upon a PCM in stance with solved parameter dependencies and known physical system states with probabilities of occurrence, our approach generates and evaluates absorbing Discrete-Time Markov Chains (DTMCs) in a recursive manner in order to predict system reliability. The algorithm has two main parts: First, an individual DTMC generation and evaluation takes places per physical system state. Second, all individual results are aggregated to gain the final result. |
| First, each behavioral specification B (usage scenario) is represented as a linear sequence of actions {A1,A2, . . .,An}, including internal actions, call actions, branches, loops, and forks, with a nested semantics. In this semantics, the whole block of behavior belonging to a branch, loop, or fork is represented with a single action, having nested behaviours. |
| After adding a START and a STOP action to the sequence, this specification is transformed into a DTMC such that each action of the behavior becomes a state of the DTMC. The START action becomes the initial DTMC state; the STOP action a SUCCESS state. Additionally, a FAILURE state is introduced to express that any action Ai can fail with probability fp(Ai). The resulting DTMC is absorbing and acyclic as shown in Fig. 3.7. The failure probability fp(B) of the overall behavior is the probability to reach the FAILURE state from the initial state: |
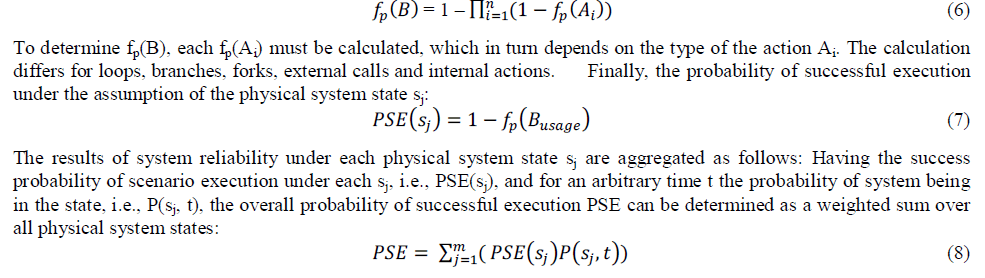 |
| Reliability evaluation is space-effective due to recursive nature of the algorithm. Given the number of resources n, the time complexity is O(2n), since there are 2n physical system states. |
CONCLUSION |
| This paper presents an approach for reliability modeling and prediction of component-based software architectures. The accuracy of the prediction is increased by integrating even the rarely included architectural aspects such as the usage profile and the execution environment. The approach is realized as an extension of the Palladio Component Model in Eclipse SDK. The PCM supports distributed, component-based systems. The prediction is validated by simulating the software. |
| The major drawback of the proposed approach is the scalability. Due to exponential complexity, the algorithm is efficient only for a maximum of approximately 20 resources. One of our future works includes addressing this scalability issue. Also the Discrete Time Markov Chains (DTMCs) that model the individual usage scenarios are not accurate because they assume constant failure probabilities between each of the states, which is not true. We will address this issue by using Continuous Time Markov Chains (CTMCs). Another assumption leading to inaccuracy of results is that the software failure probabilities of the components are assumed to be independent of each other, whereas, in practice, the failure of a software component correlates with other components. |
References |
|