ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Abdussalam Ali Ahmed Omar1 and Başar Özkan2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper presents evaluation of effect of in-wheel electric motors mass on the performance of active suspension system by using one of more common control methods which is Linear Quadratic Regulator (LQR).Unsprung mass is one of the important parameters which effects on road holding and ride comfort behaviors in the vehicles, this effect obtained in this work by comparing the performance of the system using standard tire and tire with In-Wheel Electric Motor. Also,modeling and simulation of quarter car model completed to construct the Simulink model of the system using MATLAB software. The study summarized bad effect of increasing the weight of tires by add In-Wheel Motors to the system on the road traction and the vehicles drivers comfort, at the same time the suspension system with in-wheel motor needs high actuator force to work compared to the same system without inwheel motor
Keywords |
| Suspension system, Unsprung mass, In-wheel motors, Quarter car model, Linear Quadratic Regulator ,Simulink model. |
INTRODUCTION |
| For many years vehicle dynamics engineers have struggled to achieve a compromise between vehicle handling, ride comfort and stability. The results of this are clear in the vehicles we see today. In general, at one extreme are large sedan and luxury cars with excellent ride qualities but only adequate handling behavior. At the other end of the spectrum are sports cars with very good handling but very firm ride quality. In between are any number of variations dictated by the vehicle manufacturer and target customer needs,[2]. |
| Every automotive suspension has two goals: passenger comfort and vehicle control. Comfort is provided by isolating the vehicle’s passengers from road disturbances like bumps or potholes. Control is achieved by keeping the car body from rolling and pitching excessively, and maintaining good contact between the tire and the road. |
| By and large, today’s vehicle suspensions use hydraulic dampers (a.k.a. ”shock absorbers”) and springs that are charged with the tasks of absorbing bumps, minimizing the car’s body motions while accelerating, braking and turning and keeping the tires in contact with the road surface. Typically, these goals are somewhat at odds with each other. Luxury cars are great at swallowing bumps and providing a plush ride, but handling usually suffers as the car is prone to pitch and dive under acceleration and braking, as well as body lean (or ”sway”) under cornering think Lincoln Town Car. |
| On the other end of the spectrum, stiffly sprung sports cars exhibit minimal body motion as the car is driven aggressively, as cornering is flat, but the ride quality generally suffers think Mazda Miata. Yes, there are a number of current vehicles that do a good job of providing an agreeable balance of ride and handling, such as a BMW 5 Series, the C6 Corvette and even the Cadillac SRV SUV. But Dr. Bose’s goal was to offer a suspension design that would provide an even smoother ride than a top luxury car (such as the Lexus LS430 sedan) while simultaneously providing more body control than a top sports car (such as a Porsche 911). |
| Unfortunately, these goals are in conflict. In a luxury sedan the suspension is usually designed with as emphasis on comfort, but the result is a vehicle that rolls and pitches while driving and during turning and braking. In sport cars, where the emphasis is on control, the suspension is designed to reduce roll and pitch, but comfort is scarified. |
| A typical vehicle suspension is made up of two components: a spring and a damper. The spring is chosen based solely on the weight of the vehicle, while the damper is the component that defines the suspensions placement on the compromise curve. Depending on the type of vehicle, a damper is chosen to make the vehicle perform best in its application. Ideally, the damper should isolate passengers from low-frequency road disturbances and absorb high frequency road disturbances. Passengers are best isolated from low-frequency disturbances when the damping is high. However, high damping provides poor high frequency absorption. Conversely, when the damping is low, the damper offers sufficient high-frequency absorption, at the expense of low-frequency isolation. The need to reduce the effects of this compromise has given rise to several new advancements in automotive suspensions. Three types of suspensions that will be reviewed here are passive, fully active, and semi-active suspensions,[3]. |
MATERIALS AND METHODS |
| The study aims to analyze the effect of In-Wheel electric motor mass on the active suspension system using quarter car model which basically contents of sprung mass, unsprung mass, dampers, springs ,and actuator. To achieve the target of this work, the unsprung mass will considered as two states ,the first one is a standard tire and the other one is In-Wheel motor tire. |
| The analysis of this study needs some steps to obtain the effect of In-Wheel motor mass on active suspension system which are modeling and simulation of the active suspension system, building the Simulink model of the system by Matlab software, and using linear quadratic control method(LQR). |
IN-WHEEL MOTOR STRUCTURE |
| The in-wheel electric motor (also called wheel motor, wheel hub drive, hub motor or wheel hub motor) is an electric motor that is incorporated into the hub of a wheel and drives it directly. |
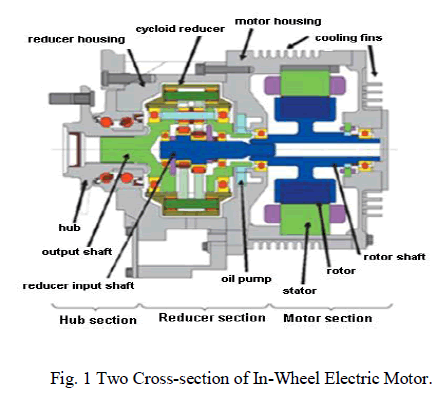
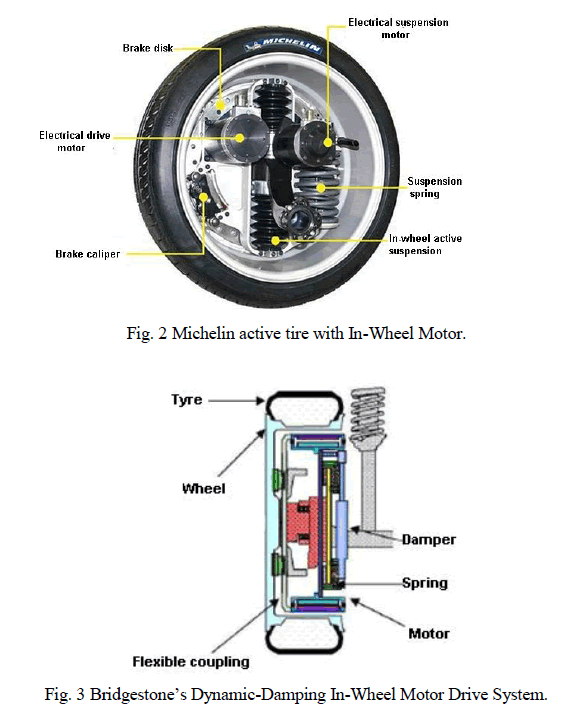
| In this work, only the effect of mass of the electric motor will take into account. Figure(1) is a cross-section of the inwheel electric motor system, which has a structure that aligns the hub, reducer section and the motor section in a series configuration. Figures(2)and(3).show the Michelin active tire with in-wheel motor and Bridgestone’s Dynamic- Damping In-wheel motor drive system. |
 |
 |
ACTIVE SUSPENSION SYSTEM MATHIMATICAL MODEL |
| Designing a suspension system is an interesting and challenging control problem. Also, Suspension system modeling serves two purposes: understanding system dynamics and developing control strategies. Models are simplified representations of physical systems, allowing focus on important system dynamics. |
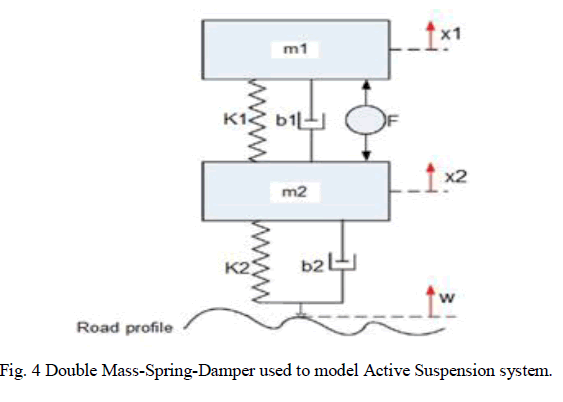
| When the suspension system is designed, a quarter car model (one of the four wheels) is used to simplify the problem to a 1D multiple spring-damper system. A diagram of this system is shown below in figure(4). This model is for an active suspension system where an actuator is included that is able to generate the control force F to control the motion of the vehicle body. |
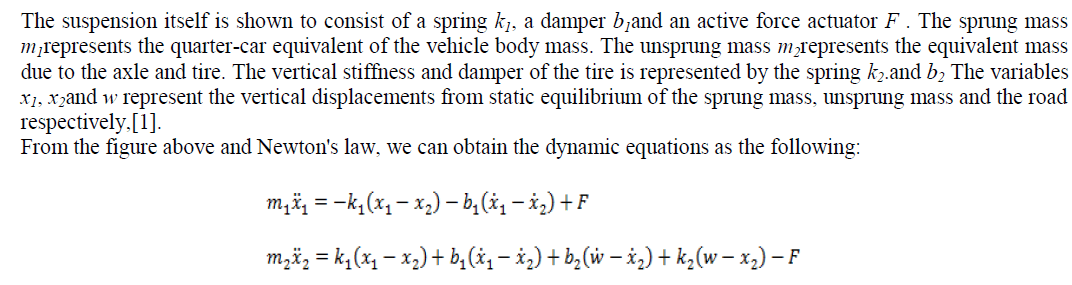 |
 |
SYSTEM PARAMETERS |
 |
SIMULINK MODEL OF THE SYSTEM |
| Figure (5) shows The Simulink model of the active suspension system of quarter car model which built by using the two previous equations. |
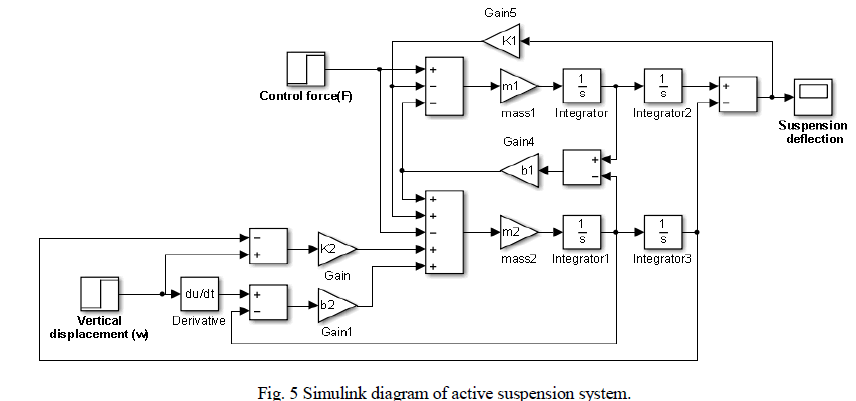 |
| The result of the Simulink model above in figure(6) is the Open-Loop Response to 0.1 m Step Disturbance of active suspension system. |
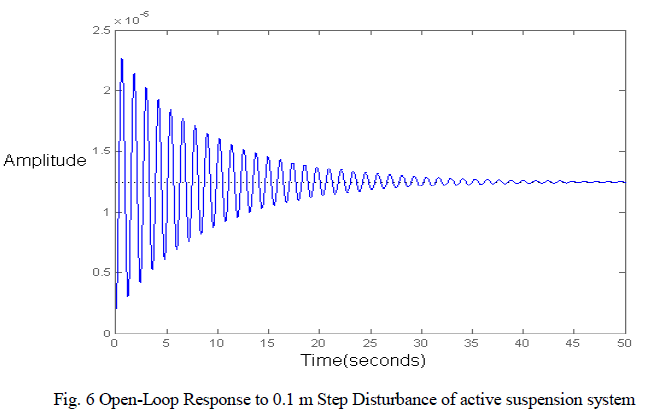 |
| Observing the figure, it is necessary to improve the response of the suspension system through the control of the suspension control force F. the control method which will use to create the controller in this work is TheLinear Quadratic Regulator (LQR). |
LINEAR QUADRATIC CONTROL(LQR) |
| The theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost isdescribed by a quadraticfunctioniscalled theLQ problem. One of the main results in the theory is that the solution is provided by the linear-quadratic regulator (LQR). The LQR is an important part of the solution to the LQGproblem. Like the LQR problem itself, the LQG problem is one of the most fundamental problems in control theory,[9]. |
| To design a full state-feedback controller for the system, state-space equations should be determined and then it can use Matlab program to find the value of the controller. |
| To find the controller matrix K ,it should Add the following command to the end of m-file and run the MATLAB program. |
 |
 |
| By run the program above we can get the value of K matrix (matrix gain) to use it to improve the system response in figure(5) in .Two values of K will used which are K1= [-0.0000 1.0274 -41.1156 -2.1412] to active suspension system without in-wheel electric motor( standard tire) and K2= 1.0e+03*[-0.0000 0.0989 -4.1495 -0.2158] to active suspension system with in-wheel electric motor. |
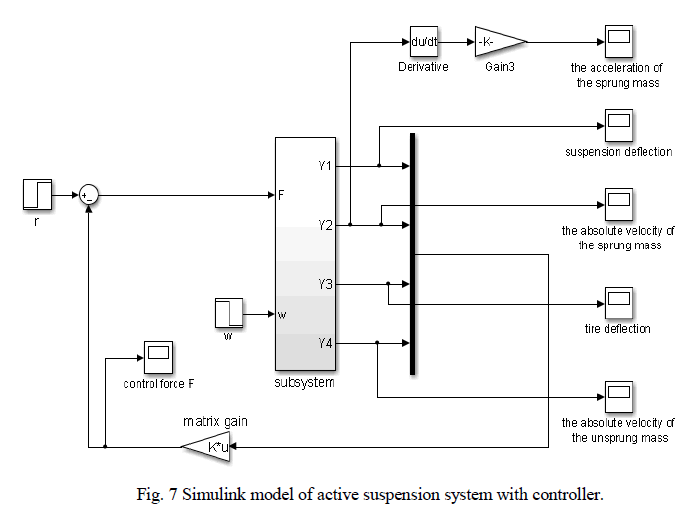 |
SIMULATION RESULTS |
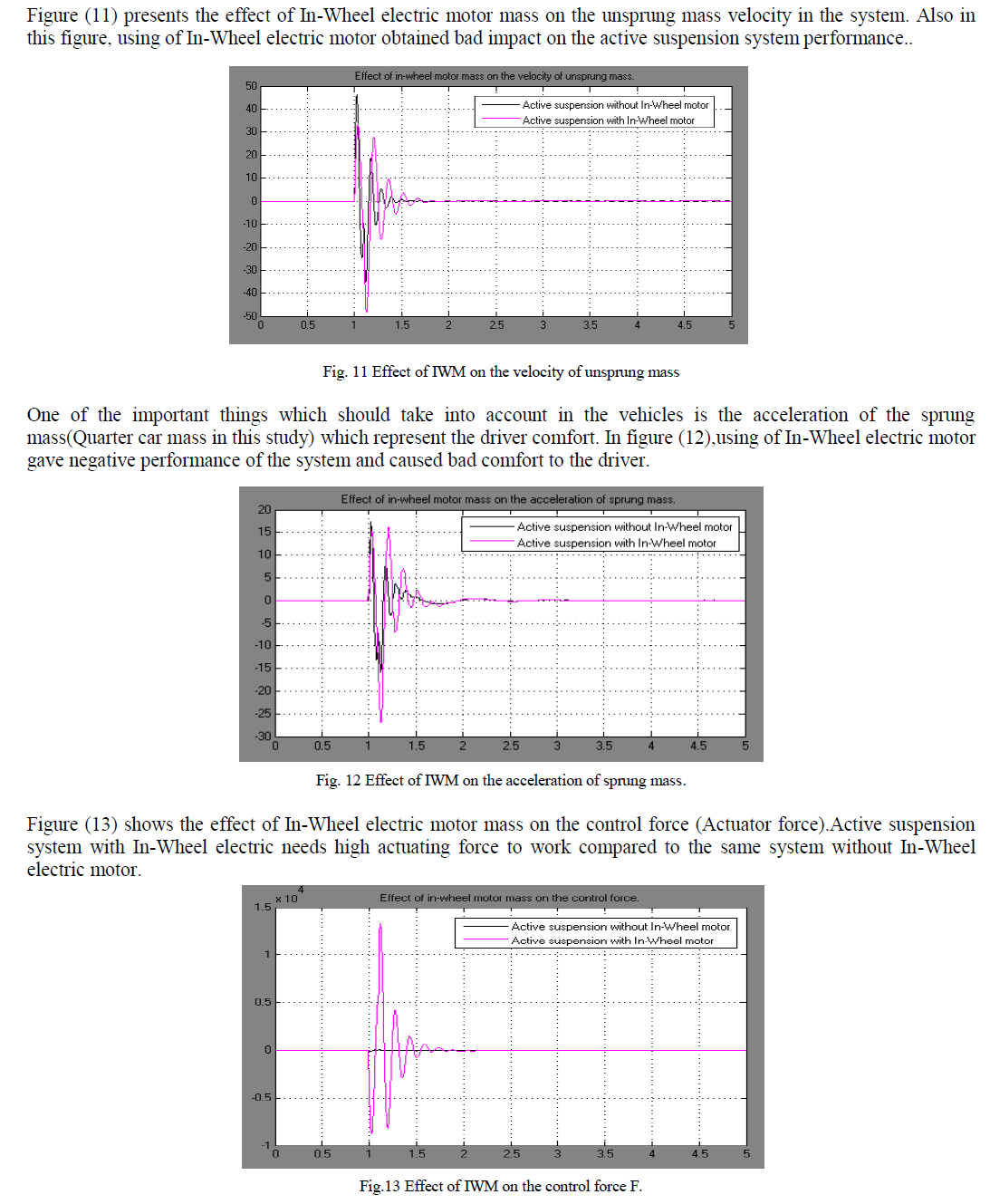
| Figures (8) to (13)show Analysis and results of active suspension system for quarter car model for speed bump of 0.1 m (step input)and the effect of in-wheel electric motor mass on the system performance. |
| Figure (8) presents the effect of In-Wheel electric motor mass on the suspension deflection of the system. it is obvious that using of In-Wheel motor increases the suspension deflection and gave bad effect of the system. |
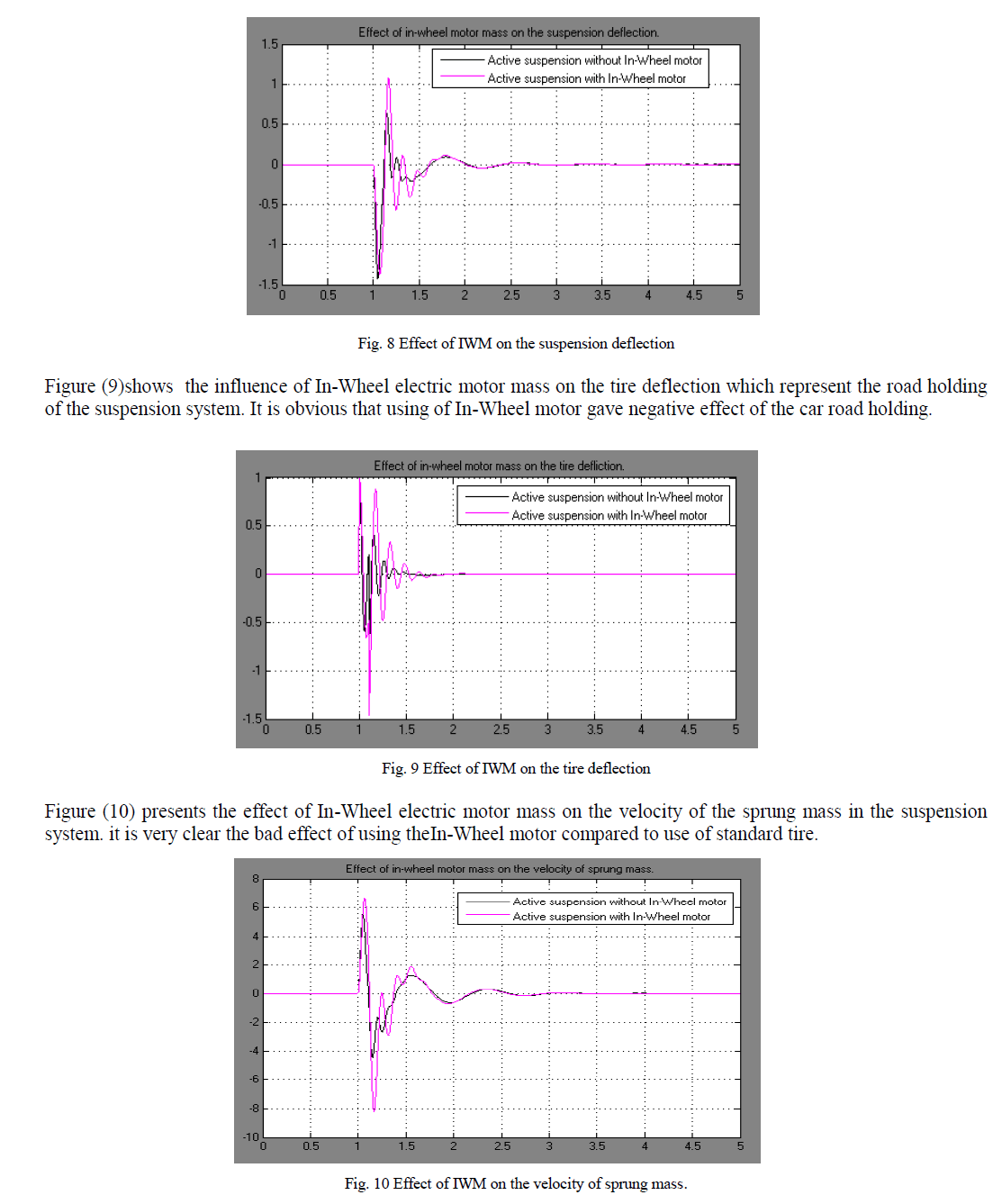 |
 |
CONCLUSION |
| This study shows a significant effect of the in-wheel electric motor mass on the active suspension system performance, some of this effect was clear on the sprung mass velocity and suspension deflection which represent the driver comfort and the road traction respectively. At same time the study explained that the active suspension with in-wheel electric motor requires high actuator force compared with the active suspension system without in-wheel motor. Finally, using of in-wheel electric motors in the vehicles has various negative aspects which caused little reliability to use it. |
References |
|