ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Mohit Kumar1 and Ram Avtar Jaswal2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In this paper, the object is to improve the reliability and overall performances of Rice Mill. When a more complexities increase in the system, the reliability evaluations become more difficult. Therefore, the derivation of symbolic reliability expression is simplified and a general system in compact form is helpful. Before this, the techniques executed earlier to solve such reliability models are very time consuming and very tedious calculations. Therefore, in this study Boolean function technique and algebra is used to evaluate systems, overall performance. Reliability of considered system has been computed by using Weibull and Exponential time distributions. M.T.T.F. of the considered system an important reliability parameter has been evaluated to develop practical utility of the model. A mathematical model has been developed with the help of Boolean function technique to measuring reliability.
Keywords |
| Boolean Function Technique, Reliability, Failure Rate, M.T.T.F, Rice Mill |
INTRODUCTION |
| Rice is considered to be staple food diet in most parts of India including east and south parts of the country. Paddy is the most important agricultural commodity in Manipur and the total area under cultivation is estimated to be 2.25 lac hectares with annual production of close to 5 lac tons. Rice is one of the chief grains of India. Thus, rice mills play very important role for human. Rice-grains consists of husk and brown rice. Brown rice in turn contain bran which comprises the outer layer and edible portion. Rice mill is removal of husk and bran to obtain edible portion for consumption .Rice mill is a crucial steps in post-production of rice. It producers edible white rice that is sufficiently milled and free form impurities. In this paper, an effort has been made to carry out the performance analysis of a rice manufacturing plant. |
| Reliability of a unit (or product) is the probability that the unit performs its intended function adequately for a given period of time under the given stated operating conditions or environment. Reliability definition stresses four element: probability, intended function, time and operating conditions [1]. Gupta P.P, Agarwal S.C have considered a Boolean Algebra Method for Reliability calculations and again Gupta P.P Kumar Arvind, Reliability and M.T.T.F Analysis of Power Plant. Sharma, Deepankar Sharma, Neelam, Evaluation of some Reliability Parameters for Tele-communication system by Boolean Function Technique [2][3][4][5]. [6][7][8][9] The reliability of several electronic equipments by using various techniques has been calculated, but the method adopted by them lead to cumbersome and tedious calculation. Keeping this fact in view, for the evaluation of various factors of reliability of Rice mill, the authors have applied Boolean function technique. |
| The block diagram of a rice mill is shown in figure 1. The work of cleaner is to remove all impurities and unfilled grains from paddy. Two identical units are working in parallel. This unit can work with one unit in reduced capacity. Husking section removes husk from paddy. Failure of this subsection causes the complete failure of the system. The separation subsystem separates the unhusked paddy from bran rice. Failure of the subsystem causes the complete failure of the system. The work of Whitening unit is to remove all or part of the bran layer and germ from brown rice. The two identical units are functioning in parallel. This unit can work with one subsystem in reduced capacity. This subsystem improves the appearance of milled rice by removing the remaining bran particles and by polishing the exterior of the milled kernel. These are two identical units. Failure of any one unit causes complete failure of the system. |
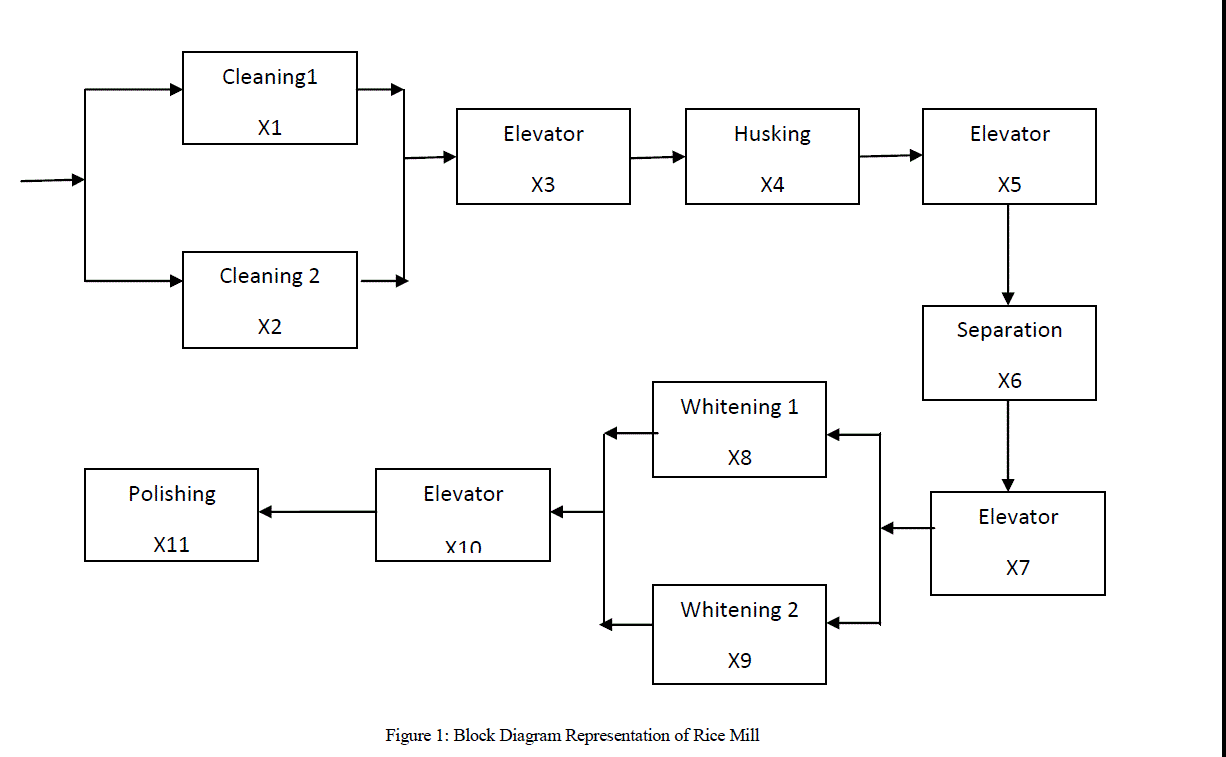 |
RELIABILITY BY BOOLEAN FUNCTION TECHNIQUE |
| The reliability of substation is determine, a mathematical model is developed as shown in figure1. Following assumptions are made for applying Boolean function technique: |
| 1. First of all , ensure all the equipments are good and operable. |
| 2. The state of all components of the system is statistically independent. |
| 3. The state of each component and as whole system operable, workable, good or fail. |
| 4. There is no repair facility. |
| 5. Supply between any two component of the system is hundred percent reliable and ok. |
| 6. The failure times of all components are arbitrary. |
| 7. The reliability of each component is to be known in advance. |
| Notations |
| X1, X2 = State of both Cleaning section |
| X3, X5, X7, X10 = State of elevator |
| X4 = State of husking section |
| X6 = State of separation of paddy from rice |
| X8, X9 = State of cleaners |
| X11 = State of polishing section |
| Xi(i = 1,2,…11) = 1 in good state and 0 in bad state |
| XiâÃâ¬ÃŸ = negation of Xi |
| ^ = Conjunction |
| ̢̢̉̉̉̉= Logical Matrix |
| Ri = Reliability of ith part of the system |
| Qi =1-Ri |
| Rs = Reliability of Whole System |
| RSW(t)/RSE(t) = Reliability of the system as a whole when failures follow Weibull /Exponential time distribution. |
FORMULATION OF MATHEMATICAL MODEL |
| The successful operation of the system in terms of logical matrix is expressed as: |
 |
 |
 |
NUMERICAL COMPUTATIONS |
| For a numerical computation, let us consider the values |
| i. Setting λi(i = 1,2,3….11) = 0.001 and in equation 15 |
| ii. Setting λi(i = 1,2,3….11) = 0.001 in equation 16 |
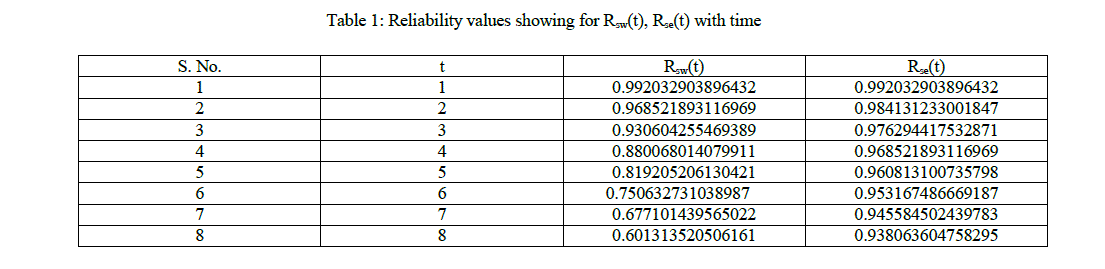
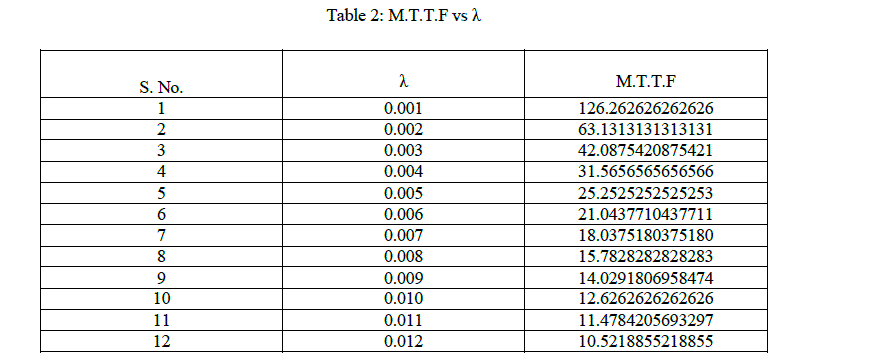
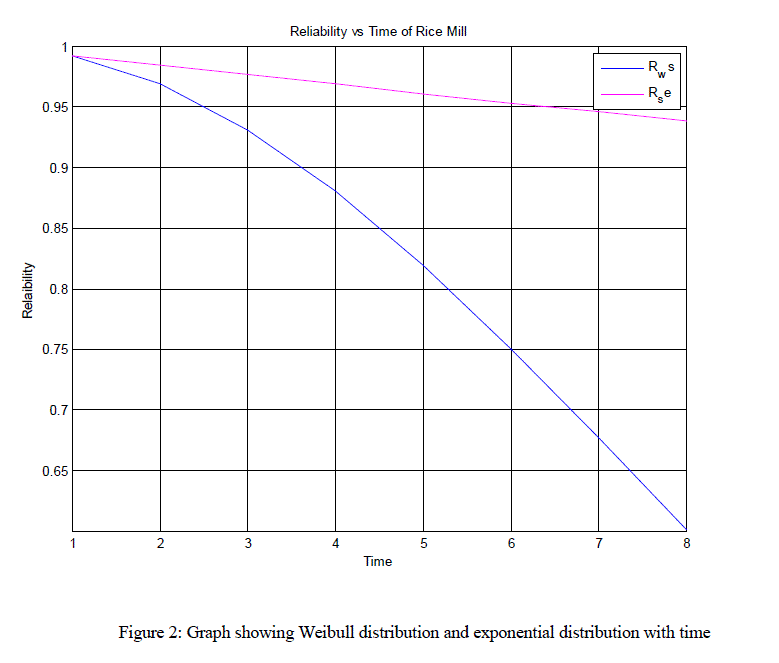
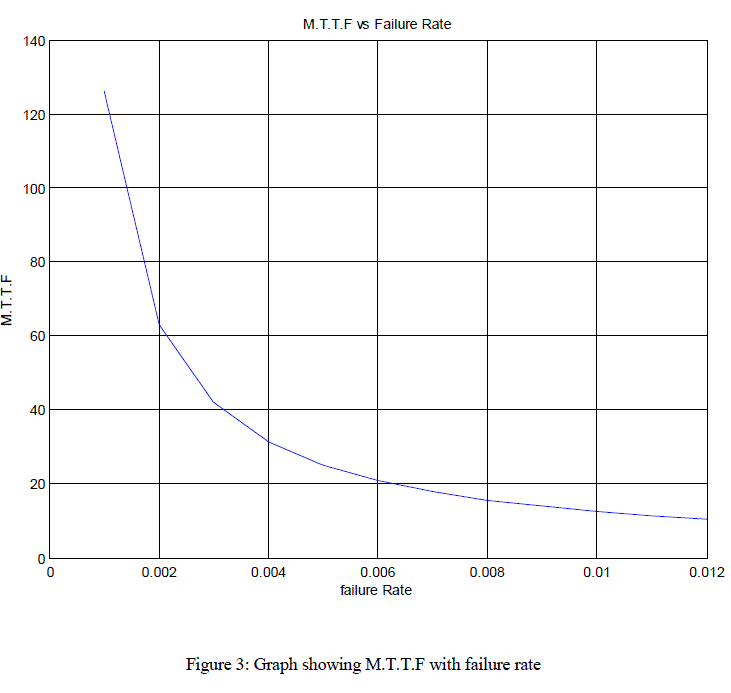
| iii. Setting λi(i = 1,2,3….11) = 0.001…….0.012 in equation 17 table 1 and table 2 has been computed and corresponding graphs are shown in figure 2 and 3 respectively. |
 |
 |
 |
 |
CONCLUSION |
| In this paper, we have considered a rice mill for analysis of various reliability parameters by employing the Boolean function technique & algebra of logics. Table 1 computes the reliability of the system with respect to time when failures rates follow exponential and Weibull time distributions. An inspection of graph “Reliability Vs Time” (fig2) reveals that the reliability of the complex system decreases approximately at a uniformly rate in case of exponential time distribution, but decreases very rapidly when failure rates follow Weibull distributions. Table 2 and graph “MTTF V/S Failure Rate”(fig-3) yields that MTTF of the system decreases catastrophically in the beginning but later it decreases approximately at a uniform rate. |
References |
|