Exhaustive to elementary proofs of Riemann hypothesis

Abstract

Riemann hypothesis stands proved in three different ways. To prove Riemann hypothesis from the functional equation concept of delta function is introduced similar to gamma and pi function. Other two proofs are derived using Eulers formula and elementary algebra. Analytically continuing gamma and zeta function to an extended domain, poles and zeros of zeta values are redefined.

Keywords

Primes; Zeta function; Gamma function; Analytic continuation of zeta function; Riemann hypothesis

Introduction

Euler the grandfather of zeta function

In 1737, Leonard Euler published a paper where he derived a tricky formula that pointed to a wonderful connection between the infinite sum of the reciprocals of all natural integers (zeta function in its simplest form) and all prime numbers [1]. Now:

 

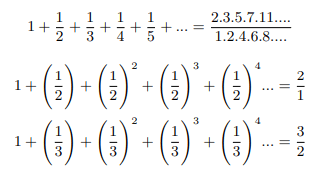
Euler product form of zeta function when s>1:

 

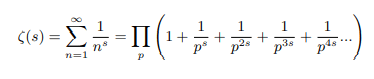
Equivalent to:

 

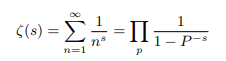
To carry out the multiplication on the right, we need to pick up exactly one term from every sum that is a factor in the product and, since every integer admits a unique prime factorization; the reciprocal of every integer will be obtained in this manner each exactly once.

MATERIALS AND METHODS

In the year of 1896 Jacques Hadamard and Charles Jean de la Valle-Poussin independently prove the prime number theorem which essentially says that if there exists a limit to the ratio of primes up to a given number and that numbers natural logarithm that should be equal to 1. When I started reading about number theory I wondered that if prime number theorem is proved then what is left. The biggest job is done. I questioned myself why zeta function cannot be defined at 1. Calculus has got set of rules for checking convergence of any infinite series, sometime especially when we are enclosing infinities to unity, those rules falls short to check the convergence of infinite series. In spite of that Euler was successful proving sum to product form and calculated zeta values for some numbers by hand only. Leopold Kronecker proved and interpreted Euler’s formula is the outcome of passing to the right sided limit as s → 1+. I decided I will stick to Grandpa Eulers approach in attacking the problem.

Riemann the father of zeta function

We can derive the following relation between zeta function and eta function which converges for all values Re(s)>0.

 

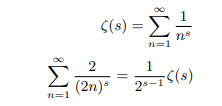
Now subtracting the latter from the former we get:

 

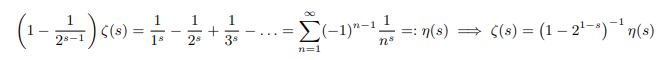
We can analytically continue zeta function from the above equation for 1≠Re(s)>0 after re-normalizing the potential problematic points as follows:

 

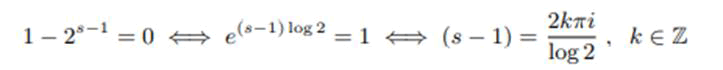
Riemann showed that zeta function have the property of analytic continuation in the whole complex plane except for s=1 where the zeta function has its pole. The zeta function satisfies Riemann’s functional equation.

 

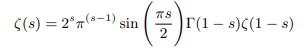
Riemann Hypothesis is all about non trivial zeros of zeta function. There are trivial zeros which occur at every negative even integer. There are no zeros for s>1. All other zeros lies at a critical strip 0<s<1. In this critical strip he conjectured that all non trivial zeros lie on a critical line of the form of z=1/2 ± iy i.e., the real part of all those complex numbers equals 1/2.

Proof of Riemann hypothesis: In this section we shall prove Riemann Hypothesis in different ways.

Proof using Riemanns functional equation

Multiplying both side of Riemanns functional equation by (s-1) we get:

 

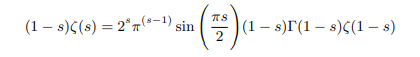
Putting (1-s)Γ(1-s)=Γ(2-s) we get:

 

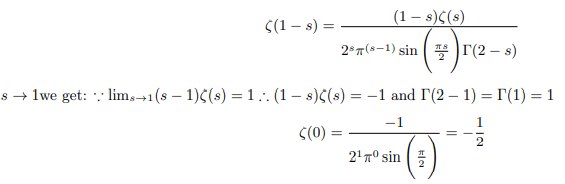
Examining the functional equation we shall observe that the pole of zeta function at Re(s)=1 is solely attributable to the pole of Gamma function. In the critical strip 0<s<1 Delta function (see explanation) holds equally good if not better for factorial function. As zeta functions have got the holomorphic property the act of stretching or squeezing preserves the holomorphic character. Using this property we can remove the pole of zeta function [2]. Introducing Delta function for factorial we can remove the poles of gamma and pi function and rewrite the functional equation as follows:

 

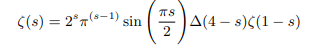
Which can be rewritten in terms of gamma function as follows:

 

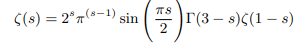
Which again can be rewritten in terms of pi function as follows:

 

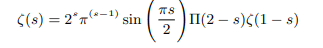
Now Putting s=1 we get:

 

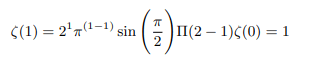
Zeta function is now defined on entire C and as such it becomes an entire function. In complex analysis, Liouville’s theorem states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f (z)| ≤ M for all z in C is constant. Being an entire function zeta function is constant as none of the values of zeta function do not exceed M=ζ(2)=π²/6 .Maximum modulus principle further requires that non constant holomorphic functions attain maximum modulus on the boundary of the unit circle. Being a constant function zeta function duly complies with maximum modulus principle as it reaches maximum modulus π²/6 outside the unit circle i.e., on the boundary of the double unit circle. Gauss’s mean value theorem requires that in case a function is bounded in some neighbourhood, then its mean value shall occur at the center of the unit circle drawn on the neighbourhood. |ζ(0)|=1/2 is the mean modulus of entire zeta function.

Inverse of maximum modulus principle implies points on half unit circle give the minimum modulus or zeros of zeta function. Minimum modulus principle requires holomorphic functions having all non zero values shall attain minimum modulus on the boundary of the unit circle. Having lots of zero values holomorphic zeta function do not attain minimum modulus on the boundary of the unit circle rather points on half unit circle gives the minimum modulus or zeros of zeta function. Everything put together it implies that points on the half unit circle will mostly be the zeros of the zeta function which all have ± 1/2 as real part as Riemann rightly hypothesized. Putting

 

 

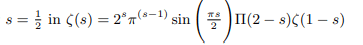
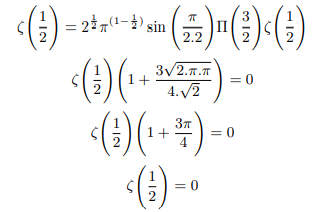
Therefore principal value of ζ(1/21) is zero and Riemann hypothesis holds good.

RESULTS AND DISCUSSION

Explanation 1: Euler in the year 1730 proved that the following indefinite integral gives the factorial of x for all real positive numbers,

 

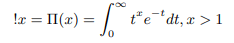
Eulers pi function satisfies the following recurrence relation for all positive real numbers [3].

 

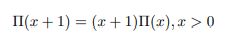
In 1768, Euler defined gamma function, Γ(x), and extended the concept of factorials to all real negative numbers, except zero and negative integers. Γ(x), is an extension of the pi function, with its argument shifted down by 1 unit.

 

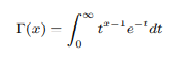
Eulers gamma function is related to Pi function as follows:

 

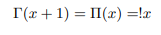
Now let us extend factorials of negative integers by way of shifting the argument of gamma function further down by 1 unit. Let us define delta function as follows:

 

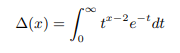
The extended delta function shall have the following recurrence relation.

 

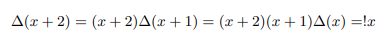
Newly defined delta function is related to Euler’s gamma function and pi function as follows:

 

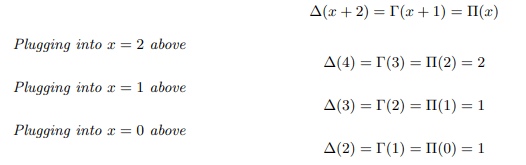
Plugging into x=-1 above us can remove poles of gamma and pi function as follows:

 

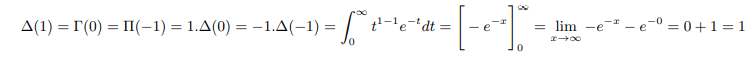
Therefore we can say Δ(-1)=-1. Similarly plugging into x=-2 above:

 

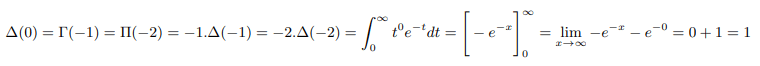
Therefore we can say Δ(-2)=-1/2. Continuing further we can remove poles of gamma and pi function: Plugging into x=-3 above and equating with result found above:

 

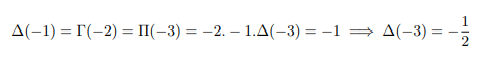
Plugging into x=-4 above and equating with result found above

 

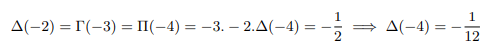
Plugging into x=-5 above and equating with result found above

 

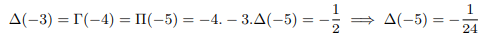
Plugging into x=-6 above and equating with result found above

 

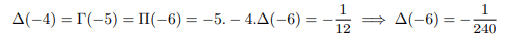
Plugging into x=-7 above and equating with result found above

 

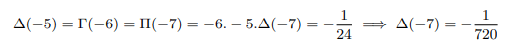
Plugging into x=-8 above and equating with result found above

 

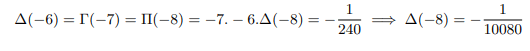
And the pattern continues up to infinity [4].

Explanation 2: Multiplying both side of Riemann’s functional equation by (s-1) we get:

 

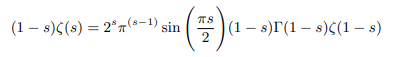
Similarly multiplying both numerator and denominator right hand side of Riemanns functional equation by (1-s)(2-s) before applying any limit we get:

 

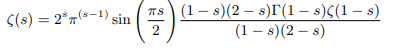
Putting (1-s)(2-s)Γ(1-s)=Γ(3-ss) we get:

 

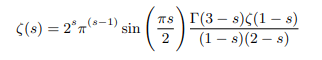
Multiplying both side of the above equation by (1-s) we get:

 

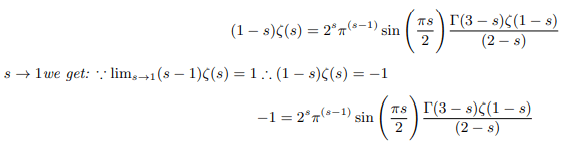
Multiplying both side of the above equation further by (2-s) we get:

 

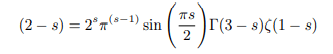
Multiplying both side of the above equation by ζ(s-2) we get:

 

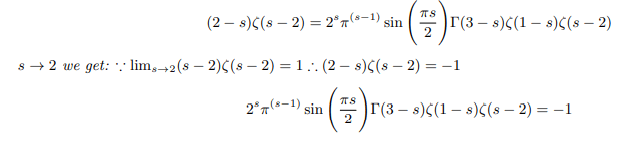
If we can set ζ(s-2)=1 then we can write:

 

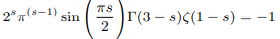
To manually define zeta function such a way that it takes value 1 or mathematically expressed as:

 

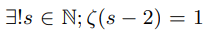
Euler’s induction approach was applied and it was observed that zeta function have the potential unit value as demonstrated in the section 4.1 and 3.4 [5]. Both the above boxed forms are numerically equivalent to Riemann’s original functional equation therefore for positive unit argument functional equation can be analytically continued as:

 

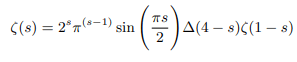
Which can be rewritten in terms of gamma function as follows:

 

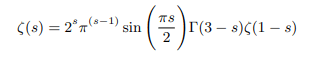
Which again can be rewritten in terms of pi function as follows:

 

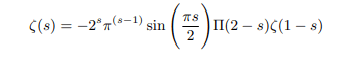
Justification of the definition we set for ζ(3-2)=1 and consistency of the above forms of functional equation have been cross checked in the main proof and also it was found that the proposition complies with all the theorems used in complex analysis [6]. Having showed that the zeta function can take unit value, multiplying both side any of the boxed equations by -1 we can analytically continue the functional equation applicable for negative arguments as follows:

 

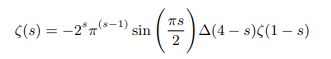
Which can be rewritten in terms of gamma function as follows:

 

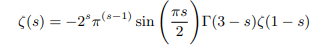
Which again can be rewritten in terms of pi function as follows:

 

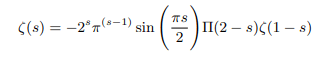
Justification of the definition we set for ζ(-1)=1/2 and consistency of the above forms of functional equation have been cross checked in the in the section 4.2. ζ(-1)=1/2 must be the second solution to ζ(-1) apart from the known Ramanujan’s proof ζ(-1)=-1/121. One has to accept that following the zeta functions analytic behaviour zeta values can be multivalued [7].

Proof using Eulers original product form

Eulers product form of zeta function in Eulers exponential form of complex numbers is as follows:

 

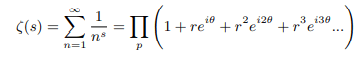
Now any such factor will be zero if:

 

 

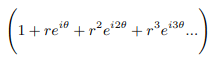
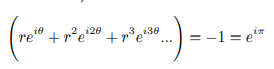
Comparing both side of the equation and equating left side to right side on the unit circle we can say:

 

We can solve θ and r as follows:

 

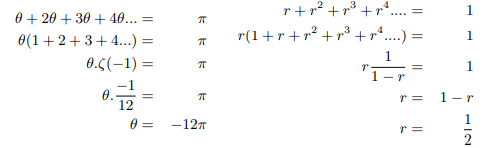
We can determine the real part of the non trivial zeros of zeta function as follows:

 

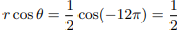
Therefore principal value of ζ(1/2) will be zero, hence Riemann hypothesis is proved:

Explanation 3: We can try back the trigonometric form then the algebraic form of complex numbers do the summation algebraically and then come back to exponential form as follows:

 

 

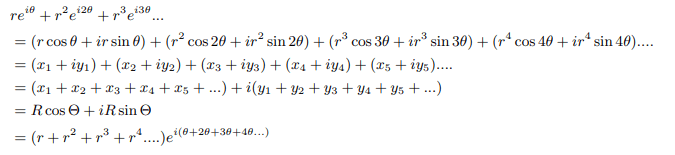
Proof using alternate product form

Eulers alternate Product form of zeta function in Eulers exponential form of complex numbers is as follows:

 

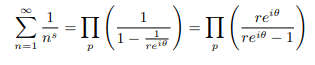
Multiplying both numerator and denominator by re^iθ +1 we get:

 

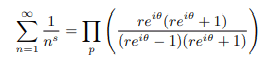
Now any such factor will be zero if reiθ(re^iθ+1) is zero:

 

 

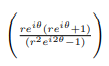
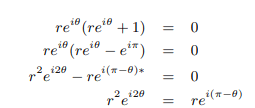
We can solve θ and r as follows:

 

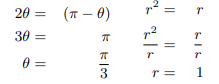
We can determine the real part of the non trivial zeros of zeta function as follows:

 

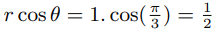
Therefore principal value of ζ(1/2) will be zero, and Riemann hypothesis is proved.

Explanation 6: e ^i(-θ) is arrived as follows:

 

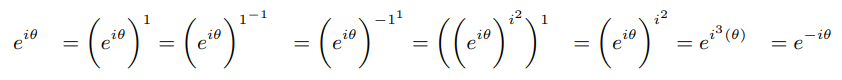
Explanation 7: Essentially proving log2(1/2 )=-1 in a complex turned simple way is equivalent of saying log(1)=0 in real way. Primes other than 2 satisfy logp(1/2)=e^iθ also in a pure complex way.

Counter proof on Nicole Oresme’s proof of divergent harmonic series

Nicole Oresme in around 1350 proved divergence of harmonic series by comparing the harmonic series with another divergent series. He replaced each denominator with the next largest power of two [8].

 

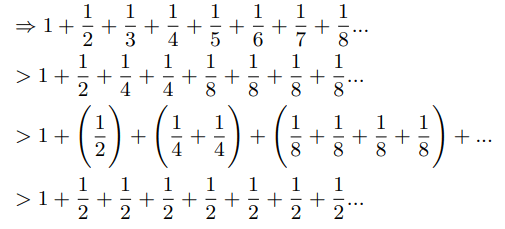
He then concluded that the harmonic series must diverge as the above series diverges. It was too quick to conclude as we can go ahead and show:

 

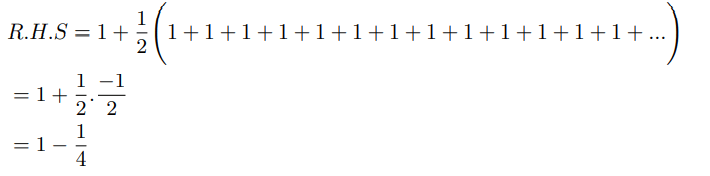
If we consider ζ(1)=1 then also it passes the comparison test.
Therefore we need to come out of the belief that harmonic series diverges. Continuing further we can show:

 

 

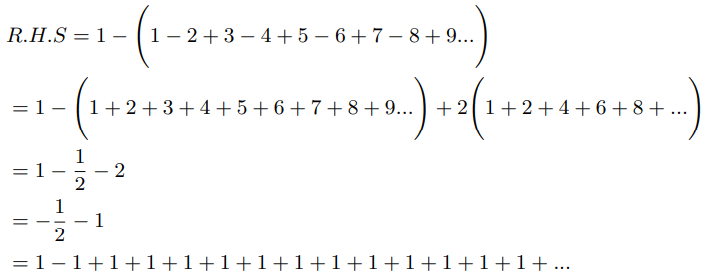
Infinite product of zeta values

Infinite product of positive zeta values converges

 

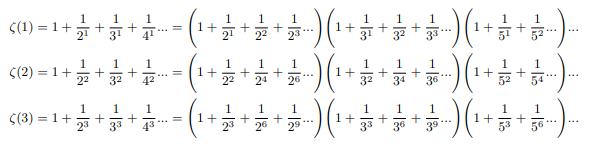
From the side of infinite sum of negative exponents of all natural integers:

 

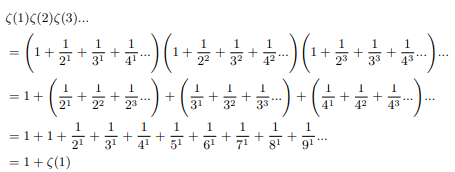
From the side of infinite product of sum of negative exponents of all primes

 

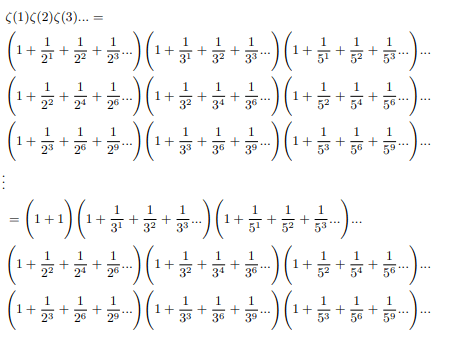
Simultaneously halfing and doubling each factor and writing it sum of two equivalent forms:

 

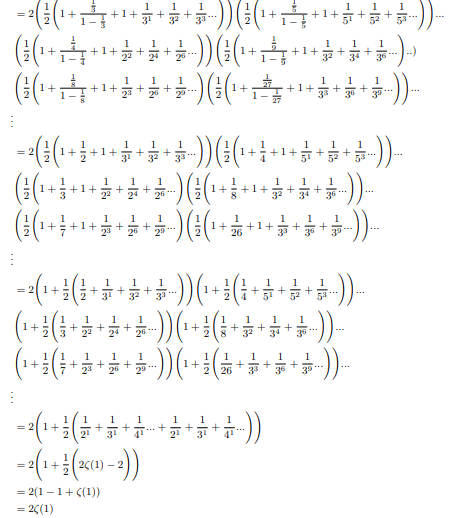
Now comparing two identities:

 

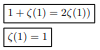
Hence Infinite product of positive zeta values converges to 2.

Infinite product of negative zeta values converges

 

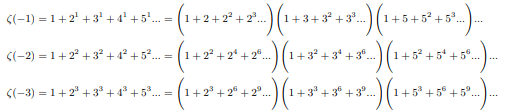
From the side of infinite sum of negative exponents of all natural integers:

 

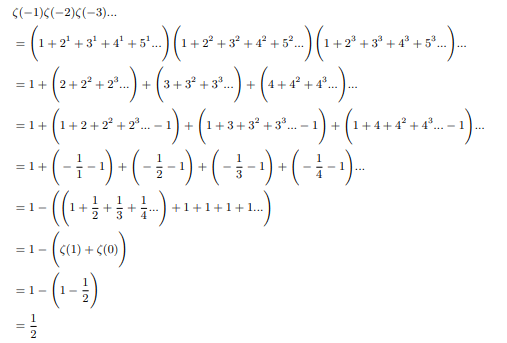
From the side of infinite product of sum of negative exponents of all primes:

 

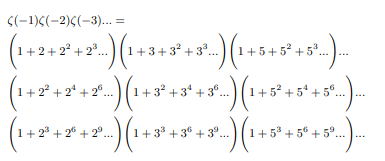
Therefore ζ(-1)=1/2 must be the second solution of ζ(-1) apart from the known one ζ(-1)=-1/12.

Using delta function instead of gamma function we can rewrite the functional equation applicable for negative argument as follows:

 

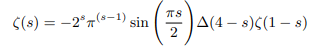
This can be rewritten in terms of gamma function as follows:

 

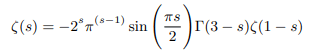
This again can be rewritten in terms of pi function as follows:

 

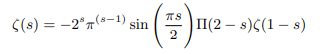
Putting s=-1 we get:

 

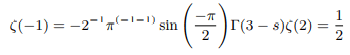
To proof Ramanujans way

 

Subtracting the bottom from the top one we get:

 

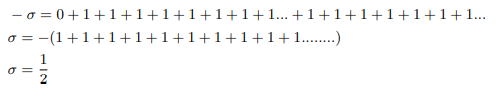
The second part is calculated subtracting bottom from the top before doubling [9].

Negative even zeta values redefined as:

 

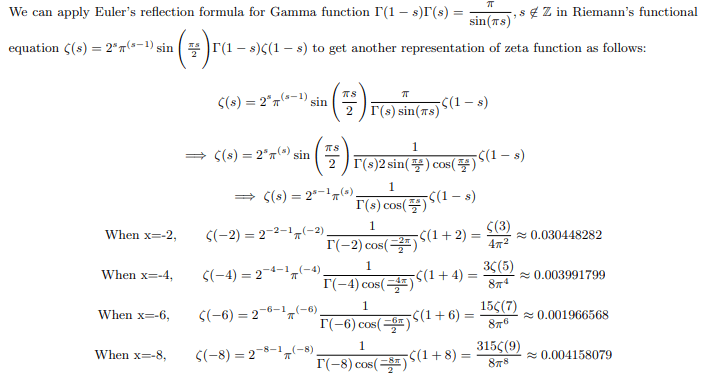
And the pattern continues for all negative even numbers up to negative infinity.

Negative odd zeta values redefined

Earlier we found that following harmonic conjugate theorem Riemann’s functional equation which is an extension of real valued zeta function can also be represented as its harmonic conjugate function which mimics the extended function [10].

 

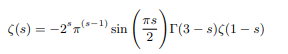
We can get the harmonic conjugates of negative zeta values as follows:

 

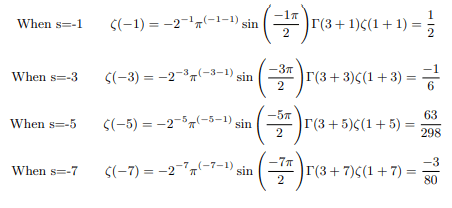
And the pattern continues for all negative odd numbers up to negative infinity.

CONCLUSION

We can conclude that Riemann hypothesis is true.

BIBILOGRAPHY

Contents freely available on internet were referred for this research work. Notable few are listed here.

References

1. Burnol JF. Two complete and minimal systems associated with the zeros of the Riemann zeta function. J Theor Nr Bordx. 2004;16:65-94.

   [Googlescholar][Indexed]

2. Merca M. New convolutions for complete and elementary symmetric functions. Integral Transforms Spec Funct. 2016;27:965-973.

   [Crossref][Googlescholar]

3. Cheer AY, et al. Simple zeros of the Riemann zeta-function. Proc Amer Math Soc. 1993;365-372.

   [Googlescholar][Indexed]

4. Goss D. A Riemann hypothesis for characteristic pL-functions. J Number Theory. 2000;82:299-322.

   [Crossref][Googlescholar][Indexed]

5. Smale S. Mathematical problems for the next century. Math Intel. 1998;20:7-15.

   [Googlescholar]

6. Chang JT, et al. Ladder heights, Gaussian random walks and the Riemann zeta function. Ann Probab. 1997:787-802.

   [Googlescholar][Indexed]

7. Saidak F, et al. On the modulus of the Riemann zeta function in the critical strip. Mathematica Slovaca. 2003;53:145-172.

   [Googlescholar]

8. Goldston DA. On the function S (T) in the theory of the Riemann zeta functions. J Number Theory. 1987;27:149-77.

   [Crossref][Googlescholar]

9. Bruggeman RW, et al. A new approach to the spectral theory of the fourth moment of the Riemann zeta-function.

   [Googlescholar]

10. Csordas G, et al. Moment inequalities and the Riemann Hypothesis. Constr Approx. 1988;4:175-198.

    [Googlescholar][Indexed]