ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
S.Sathiya Priya1 and Dr.N.R.Alamelu2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In this paper, we describe about the low complexity and good performance for medium signal to noise ratio signals. Due to practical implementation maximum likelihood is more complex, hence here we proposed expectation maximization algorithm for best design of channel estimation and receiver design. The efficiency of this algorithm can be investigated with simulation using Matlab.
Keywords |
| Time hopped pulse position modulation, Cramer Rao lower bound, Expectation Maximization, Rake receiver, Gaussian mixture, UWB Channel estimation, Least Mean Square. |
INTRODUCTION |
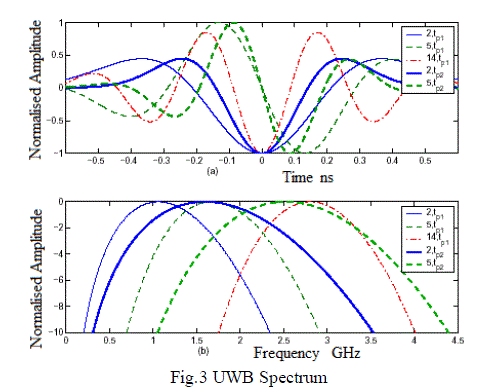
| Ultra-wide band communications (UWB) made drastic change in the world of communication. UWB used in the applications where high data transmission rate required in a short range. These systems spread the information over a wide transmission bandwidth of frequency about 500MHz. But it uses a low spectral density of transmission power about 0.5mW. The ultra wide band also called as impulse, Non-Sinusoidal pulse, Carrier less communications. UWB communication is realized by time hopping impulse radio. It consists of simple transmitter structure that contains of pulse generator (to generate Gaussian pulse), PN sequence Code generator (to generate unique code for each user) and Mixer etc. But the UWB receiver is considerably complex, which needs rake receiver in the multipath environment. Digital implementation of rake receiver requires very high sampling processing speed in both channel estimation and data detection. Hence modified rake receiver is recently proposed. This paper introduced a receiver and training structure that can obtain the complete information about the channel with low complexity. |
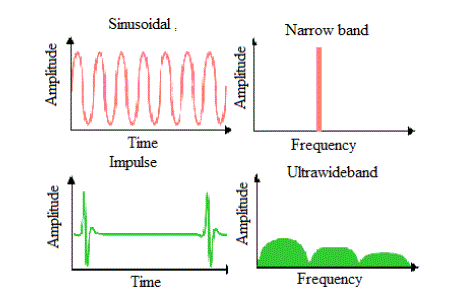 |
| Fig.1 UWB pulse in time Domain and Frequency Domain UWB system consist of UWB is only defined with respect to the bandwidth of the radiated signal. Pulse is the unique label of UWB systems. |
| UWB signals have excellent temporal and spatial resolution ability and wall penetrating ability (in some spectrum). This could open many new applications with locating function. UWB provides a potential carrier-less solution. |
UWB CHALLENGES |
| 1. Complex propagation properties, including waveform distortion due to frequency dependent propagation, dense multipath signals with low energy, make system design difficult. |
| 2. Stringent timing requirement demands algorithms with fast processing speed, low complexity and timing error robustness. |
| 3. Large bandwidth implies the necessities of high sampling rate and advanced narrowband interference suppression algorithms. |
| 4. Many advanced features of UWB signals, such as low duty cycle, large bandwidth, multipath immunity and inherent full digital solution, can be exploited. |
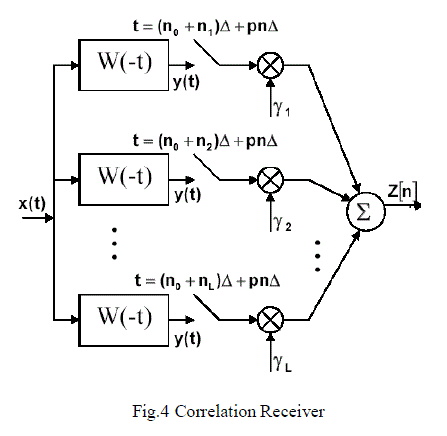
| Several channel parameters determination is important requirements for Rake receiver design change in the UWB case: |
| 1.Accuracy of channel parameters and method of determination parameters is crucial. |
| 2.Not only the transmitted power but also the shape of radiated spectrum has to be controlled. |
| 3. Some critical performance factors of receiver, such as phase dispersion, peak pulse amplitude (efficiency), pulse width (data rate), and omni-directional impulse, are hard to be satisfied by general characterization methods. |
PRINCIPLE OF EM ALGORITHM |
| The EM algorithm is used to find the maximum likelihood parameters of a statistical model where the equations cannot be solved directly. These models relate latent variables, Unknown parameters and known data observations. The model can be constructed simply by assuming the existence of additional unobserved data points. |
| The EM algorithm proceeds from the observation that the following is a way to solve these two sets of equations numerically. |
| One can simply pick arbitrary values for one of the two sets of unknowns, use them to estimate the second set, then use these new values to find a better estimate of the first set, and then keep alternating between the two until the resulting values both converge to fixed points. It's not obvious that this will work at all, but in fact it can be proven that in this particular context it does, and that the derivative of the likelihood is (arbitrarily close to) zero at that point, which in turn means that the point is either a maximum or a saddle point. In general there may be multiple maxima, and there is no guarantee that the global maximum will be found. Some likelihood also has singularities in them, i.e. nonsensical maxima. For example, one of the "solutions" that may be found by EM in a mixture model involves setting one of the components to have zero variance and the mean parameter for the same component to be equal to one of the data points. |
| Useful if hidden data, and if analysis is more tractable when 0/1 hidden data z known |
| Iterate: |
| E-step: estimate E(z) for each z, given θ |
| M-step: estimate θ maximizing E(log likelihood) |
| given E(z) [where “E(logL)” is with respect to random z ~ E(z) = p(z=1)] The EM algorithm will converge very slowly if a poor choice of initial value were used. Indeed, in some cases where the likelihood is unbounded on the edge of the parameter space, the sequence of estimates generated by the EM algorithm may diverge if is chosen too close to the boundary. Also, with applications where the likelihood equation has multiple roots corresponding to local maxima, the EM algorithm should be applied from a wide choice of starting values in any search for all local maxima. A variation of the EM algorithm uses interval analysis methods to locate multiple stationary points of a log likelihood within any designated region of the parameter space. |
| Here, we illustrate different ways of specification of initial value within mixture models framework. For independent data in the case of mixture models of G components, the effect of the E-step is to update the posterior probabilities of component membership. Hence the first E-step can be performed by specifying a value for each , i takes the value i (i=1,2,…n) where |
 |
 |
EM ALGORITHM |
| 1. First, initialize the parameters to some random values. |
| 2. Compute the best value for Z given these parameter values. |
| 3. Then, use the just-computed values of Z to compute a better estimate for the parameters . Parameters associated with a particular value of Z will use only those data points whose associated latent variable has that value. |
| 4. Iterate steps 2 and 3 until convergence. |
| Filtering and smoothing EM algorithms arise by repeating the following two-step procedure: |
| E-step |
| Operate a Kalman filter or a minimum-variance smoother designed with current parameter estimates to obtain updated state estimates. |
| M-step |
| Use the filtered or smoothed state estimates within maximumlikelihood calculations to obtain updated parameter estimates. |
 |
LEAST SQUARE ESTIMATION |
 |
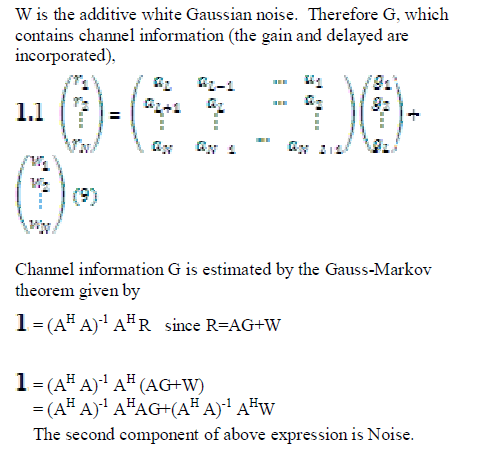 |
CHANNEL ESTIMATION METHODS IN UWB |
| The more popularly used to estimate the channel models are as follows: |
| A. Educational sequence method |
| The channel acquisition is done by available a known sequence is used. Then channel model constructed based on these sequence. The channel tracking can be pursued by re transmitting a known sequence in a regular interval. This is the best method of channel estimation but wastage power and bandwidth occurred during the transmission of training sequence. |
| B. Blind channel estimation |
| This blind channel estimation is useful in broadcast networks where training sequences would impede the transmitter. In this method which has no need of training sequence, using the covariance matrix, the receiver estimates the coefficients of channel and reveals the sent inputs by using them |
| C. Partially blind method |
| In this method the between up between properties of the two previous methods are used. |
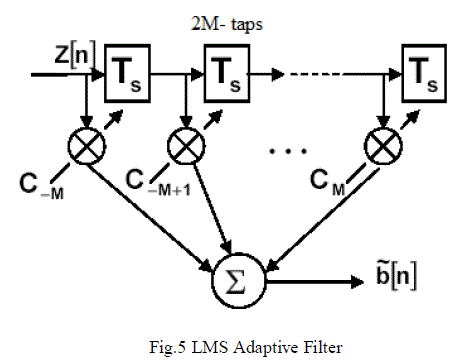 |
SIMULATIONS AND RESULTS DISCUSSIONS |
| The Least Square (LS) method was chosen for initial channel estimation in attenuations at receiver, using applicable proposed receiver, which has simple and usable structure, then channel state information was estimated by linear interpolator in information attenuations, which uses two adjacent channel estimation in delayed path to compute channel in another delayed path and LMS iterative algorithm, including a feedback of output is added to system. This algorithm uses the channel estimation of last iteration in current estimation. The recent digital transmission systems impose the application of channel equalizers with low complexity and low Bit Error Rate (BER). |
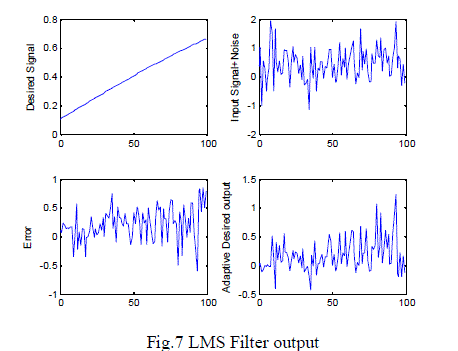 |
| Adaptive equalizers are unavoidable to satisfy these requirements. A channel equalizer is an important component of a communication system and is used to mitigate the ISI introduced by the channel. |
 |
 |
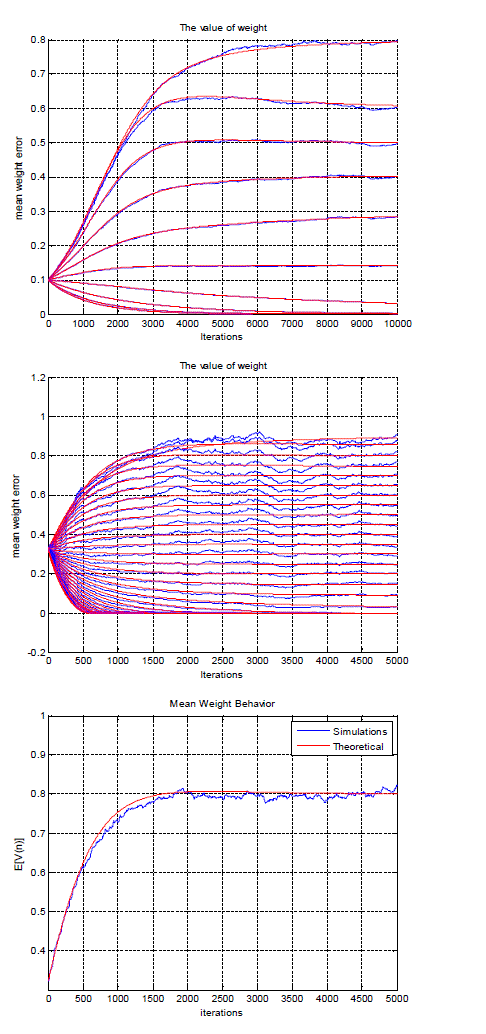
| The equalizer depends upon the channel characteristics. In a wireless channel, due to multipath fading, the channel characteristics change with time. Thus it may be necessary for the channel equalizer to track the time varying channel in order to provide reasonable performance. An adaptive equalizer is essentially a linear adaptive filter used to model the inverse transfer function of the channel. Two well-known adaptive algorithms are the (LMS) algorithm and the (RLS) algorithm. |
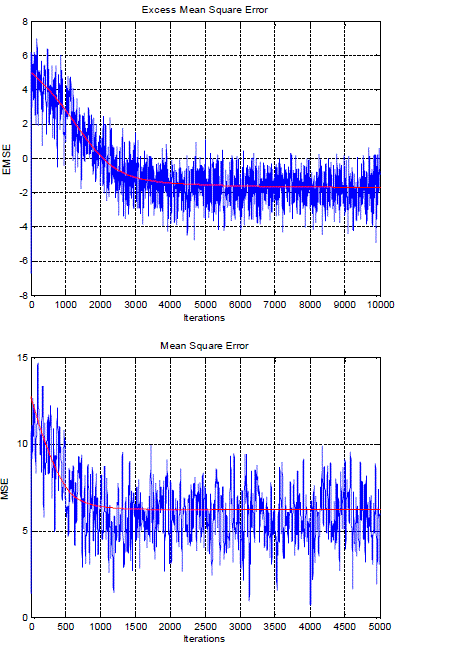 |
| Although the RLS algorithm has better convergence speed than the LMS algorithm its complexity for hardware implementation can be very high. Actually, the LMS algorithm is widely adopted in hardware implementation because of its simplicity and robustness. The LMS algorithm executes quickly but converges slowly, and its complexity grows linearly with the number of weights. On the other hand, There are some estimators in two limit modes of (NDA, DA) and one middle mode of (CA), separated from what is used as scale for estimation, related to the amount of receiver knowledge of assumed density function. The DA ML estimator does not exploit all the information available about the channel because it makes use of the data free observation samples only. To improve the channel estimate quality, the channel can be estimated on the basis of the whole received burst, including both the training sequence and the data. However, when the transmitted sequence is unknown and encoded, the likelihood function exploiting the code is much more difficult to compute. The EM algorithm enables iteratively solving this problem. The EM algorithm has been exploited previously to estimate the channel, but it has usually been used to estimate the channel taps only. |
CONCLUSION |
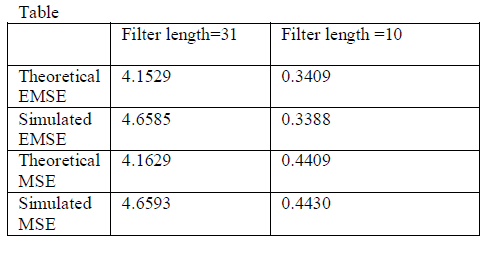
| Estimation of channel coefficients and synchronization parameters are two main challenges in realization of UWB systems. In almost all published references till no, estimation of cannel coefficients is done with the assumption of total frequency synchronously of transmitter and receiver. Therefore for exact estimation of fading channel status, it’s necessary to keep the created frequency synchronously between transmitter and receiver, uninterrupted. The MMSE channel estimation has well performance but higher complexity than least-square (LS) channel estimation. The channel autocorrelation matrix and noise variance were estimated, which could be used in the MMSE estimator. The simulation results showed that the performance of MSE in the proposed method was close to the ideal MMSE estimator and better than the LS estimator. The BER performance was also improved effectively. On the other hand, the presented EM algorithm estimates the carrier frequency offset and fading channel coefficients in two sequential steps, using the header sequence at the beginning of sent frames. The LMS method is extremely dependant to parameter, μ. This method presents appropriate channel estimation through applying simple recurrence relations. |
References |
|