In digital systems, the filters occupy a major role. This work describes the design of parallel FIR filter structures using poly-phase decomposition technique that requires minimum number of multipliers and low power adders. Normally multipliers consume more power and large area than the adders. For reducing the area, this filter structure uses adders instead of multipliers since the adder requires low power and less area than the multipliers. Moreover, number of adders does not increase along with the length of parallel FIR filter. Finally the proposed parallel FIR filter structures are beneficial in terms of hardware cost and power when compared to the existing parallel FIR filter structure.
Keywords |
| Digital signal processing (DSP), fast finite-impulse response (FIR) algorithms (FFAs),
symmetric convolution |
INTRODUCTION |
| High-performance and low-power digital signal processing (DSP) is more useful in multimedia application, because it
has explosive growth. In any digital signal processing (DSP) system, the FIR filter is one of the fundamental processing
elements for giving high performance. FIR filters are used in DSP applications such as video and image processing to
wireless communications. In video processing, the FIR filter circuit has the tendency to operate at high frequencies and
other applications, like cellular telephony and multiple-input multiple-output (MIMO), the FIR filter circuit can be
operate in moderate frequencies and also has low-power circuit with high throughput. |
| Two techniques of DSP applications like parallel and pipelining processing are used to reduce the power consumption.
Power consumption of the original filter is reduced by parallel or block processing with digital FIR filters and also
throughput is increased. Multiple outputs of parallel processing are computed by parallel in a clock period. So the level
of parallelism increases the effective sampling speed. In the parallel processing applications, hardware units are
replicated by involvement of an FIR filter and parallel functions of several inputs with several outputs can be processed
at the same time. The original circuit area is A, and the L-parallel circuit needs an area of L × A. Linearly increases the
circuit area with the block size. Due to the design area limitations, parallel processing hardware has much trouble in
design situations. So the trouble can be solved by use of parallel FIR filtering structures that consume less area than
traditional parallel FIR filtering structures. |
| Critical path is reduced due to the pipelining transformation that is introducing pipelining latches along the data path
and also it increase the clock speed or sample speed or to reduce power consumption at same speed. Power
consumption can be reduced by pipelining as similar to the parallel processing. In [5]-[11], the complexity of parallel
FIR filter is reduced by the help of poly-phase decomposition, where first derive the small-sized parallel FIR filter
structures and then the larger block-sized ones can be implemented by cascading or iterating small-sized parallel FIR
filtering blocks. The complexity of parallel filter can be removed by the use of new class of algorithms termed as Fast
FIR Algorithms (FFA) and it reduce the number of multiplications with increasing the number of additions for
implement the hardware. This approach is used for implement the L-parallel filter approximately (2L - 1) sub-filter
blocks, each having the N/L length. The resulting parallel filtering structure would require (2N – N/L) multiplications
instead of L×N. |
FAST FIR ALGORITHM |
| Assuming {xi} and {hi} to be the input sequence and FIR filter Nth-order impulse response respectively, the output
sequence yn and the filter transfer function H(z) can be written as |
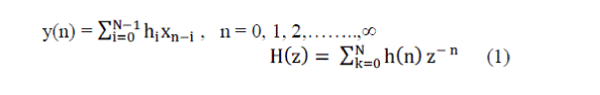 |
| The traditional L-parallel FIR filter can be implemented using poly-phase decomposition as |
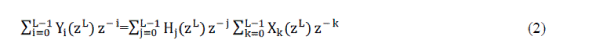 |
| where Yi(z), Xk(z), and Hj(z) are the poly-phase components of output, input, and the filter transfer function,
respectively and the poly-phase components are defined as follows, |
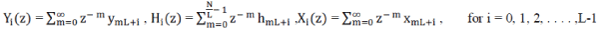 |
| The parallel FIR filter can be realized by the above block FIR filtering equation and various FFA structures are used to
reduce the linear complexity. |
| A. 2 × 2 (L = 2) FFAS |
| From the Equation (2) having theL = 2, |
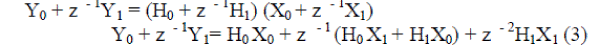 |
| which implies that |
 |
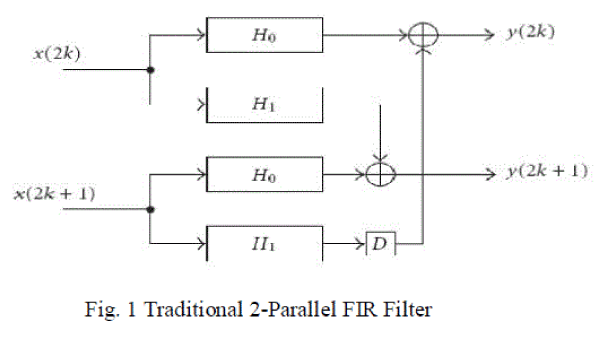
| Fig. 1 shows the direct implementation of Equation (4)and 2 outputs using 4 length N/2 FIR filters structure computes a
block and 2 post-processing additions, which requires 2N multipliers and 2N − 2 adders. |
| However, Equation (4) can be written as |
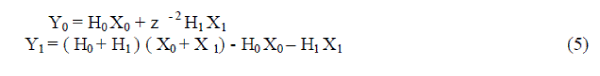 |
 |
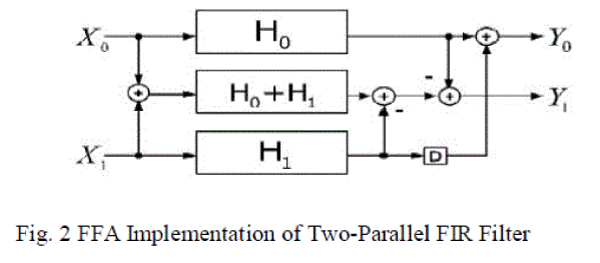 |
| The equation (5) shows the implementation in Fig. 2. This structure has three FIR sub-filter blocks of length N/2, which
requires 3N/2 multipliersand 3(N/2 − 1) + 4 adders. From the figure, this filter structure has one preprocessing and
three post-processing adders. |
| B. 3 × 3 (L = 3) FFAS |
| The (3×3) FFA produces a block size 3 parallel filtering structure. From (2) with L = 3, |
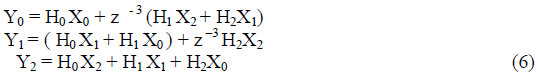 |
| Direct implementation of Equation (6) computes a block of 3 outputs using 9 length N/3 FIR filters and 6 postprocessing
additions, which requires 3N multipliers and 3N − 3 adders. By a similar approach as in (2×2) FFA,
following (3×3) FFA is obtained, |
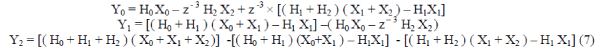 |
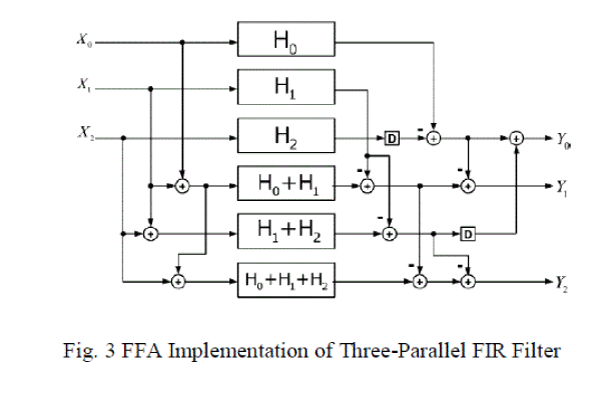
| The hardware implementation of Equation (7) requires six length N/3 FIR sub-filter blocks, three preprocessing and
seven post-processing adders, which reduce hardware cost. The implementation obtained from Equation (7) is shown in
Fig. 3. |
 |
PROPOSED FFA STRUCTURES FOR SYMMETRIC CONVOLUTIONS |
| A new structure is proposed to utilize the symmetry of coefficients. Poly-phase decomposition is manipulated to earn
many sub-filter blocks, which contain the symmetric coefficients. The sub-filter block reuses the half the number of
multiplications and the total amount of an N-tap L-parallel FIR filter with saved multipliers uses the half the number of
multiplications in a single sub-filter block (N/2L). |
| A. 2×2 PROPOSED FFA (L = 2) |
| From (4), A two-parallel FIR filter can be written as |
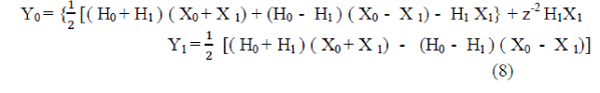 |
 |
 |
 |
 |
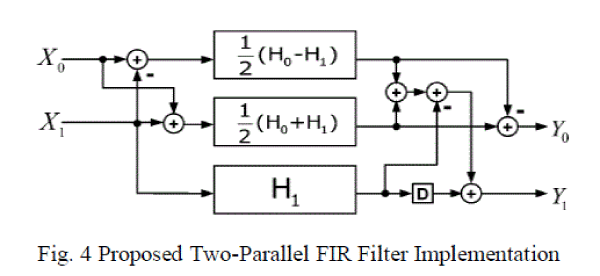
| When it comes to a set of even symmetric coefficients, Equation (8) can give one more symmetric coefficientsof subfilter
block and the proposed two-parallel FIR filter implementation shown in Fig. 4. Proposed two-parallel FIR filter
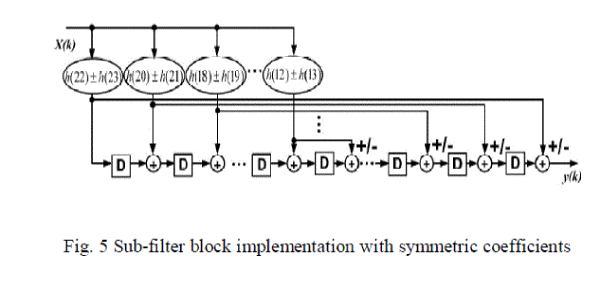
structure has three sub-filter blocks. Among those, 2 sub-filter blocks (H0 - H1 ) and (H0 + H1 ) are equipped with
symmetric coefficients can be realized by Fig. 5. So each output of multiplier responds to two taps. Compared to the
existing FFA two-parallel FIR filter structure, the proposed FFA structure needs the half of the multipliers. |
| B. 3×3 PROPOSED FFA (L=3) |
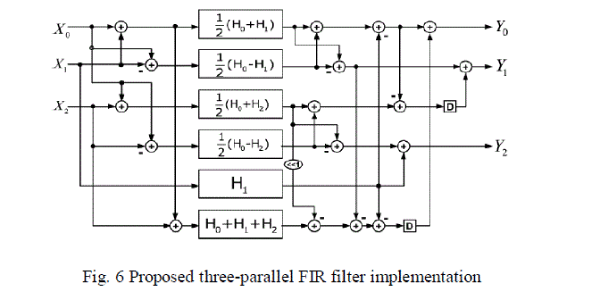
| Same as the equation (6), a three parallel FIR filter is written as equation (9). The proposed three-parallel FIR filter
structure has the four of six sub-filter blocks with symmetric coefficients. |
 |
| But the existing three parallel FIR filter structure has only two out of six sub-filter block with symmetric
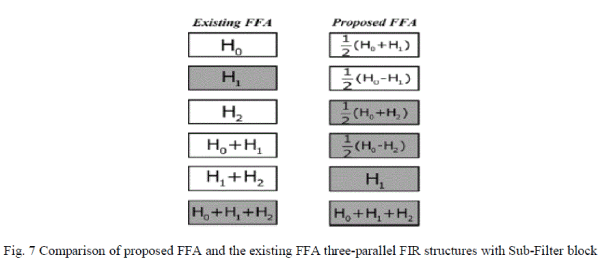
coefficients. Implementation of proposed three-parallel FIR filter structure is shown in Fig. 6. Comparison between
proposed and existing three-parallel FIR filter structure is shown in Fig. 7. where the sub-filter blocks with symmetric
coefficients shown by shadow blocks. The proposed structure additionally adds two adders in preprocessing and five
adders in post processing blocks. Therefore, N/3 multipliers can be saved for proposed N-tap three-parallel FIR filter
structure. |
| C. PROPOSED CASCADING FFA |
| The proposed parallel FIR filter structure brings more adder cost in preprocessing and post-processing blocks. It reuses
the multipliers in some part of the sub-filter blocks. For larger parallel block factor L, cascading the proposed FFA
parallel FIR structures increase the number of adders. So hardware complexity can be increased. To avoid complexity,
the existing FFA structures are employed for some sub-filter blocks that contain no symmetric coefficients which have
more compact operations in preprocessing and post-processing blocks and the proposed FFA structures are applied to
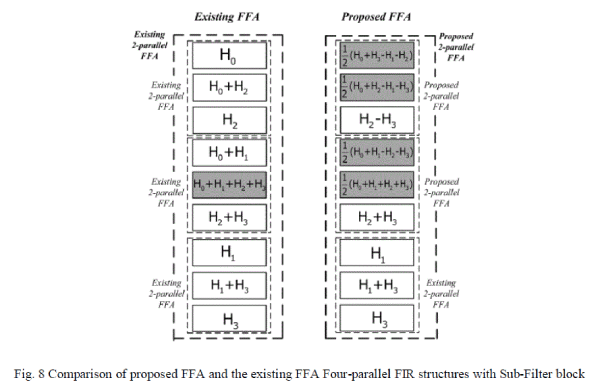
the rest of sub-filter blocks with symmetric coefficient. Comparison of sub-filter blocks between four parallel existing
FFA and proposed FFA is shown in Fig. 8. The proposed four parallel FIR structure has three more sub-filter blocks
having symmetric coefficients compared to existing FFA structure. |
EXPERIMENTAL RESULT AND IMPLEMENTATION |
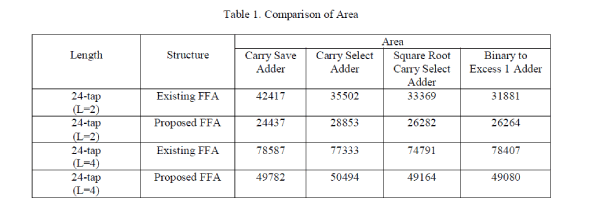
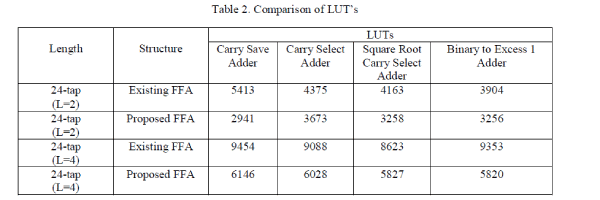
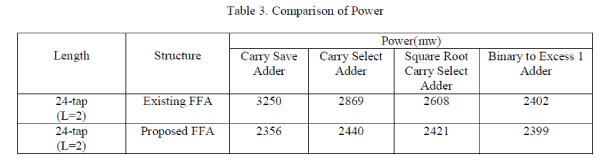
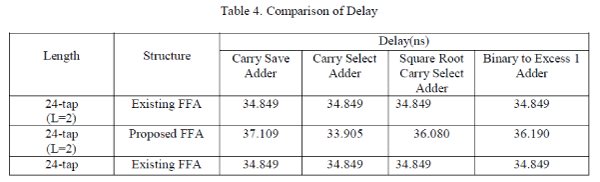
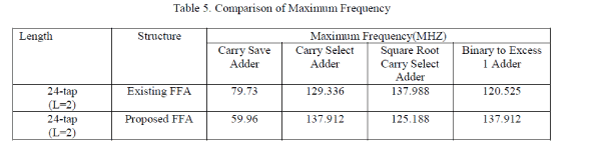
| The existing FFA structures and the proposed FFAarchitectures have been implemented in VHDL with word length 16-
bit and filter length of 24. Carry save, carry select and binary to excess 1 adder are used to implement the sub-filter
block. Parallel FIR Filter structure simulation result is shown in Fig. 9. Detailed comparison results of area, LUTS,
power, delay and Maximum frequency are showed in the Table I, Table II, Table III, Table IV, Table V. |
 |
 |
 |
 |
 |
 |
CONCLUSION |
| The proposed parallel FIR filter structure was designed to reduce the power consumption and hardware complexity. It
gives the more features to symmetric convolutions when the multiple number of taps like 2 or 3. Multiplier provides the
higher hardware consumption in implementationparallel FIR filter. This method having the symmetric coefficients
nature and saves the more amounts of multipliers with help of adders and it has high benefits. So, the proposed
structures have thesymmetric convolutions dealing with advantageous poly-phase decompositions. It gives the better
hardware consumptionthan the existing FFA structures. |
References |
- Acha, J.I. (1989), âÃâ¬ÃËComputational structures for fast implementation of L-path and L-block digital filters,âÃâ¬Ã⢠IEEE Transactions on Circuit Systems I, vol. 36, no. 6, pp. 805âÃâ¬Ãâ812.
- Cheng, C., and Parhi, K. K. (2004), âÃâ¬ÃËHardware efficient fast parallel FIR filter structures based on iterated short convolution,âÃâ¬Ãâ¢IEEE Transactions onCircuitsSystems I, Reg. Papers, vol. 51, no. 8, pp. 1492âÃâ¬Ãâ1500.
- Cheng, C., andParhi, K. K. (2005), âÃâ¬ÃËFurther complexity reduction of parallel FIR filters,âÃâ¬Ã⢠in Proc. IEEE International Symposium on Circuits Systems I, Kobe, Japan,
- Cheng, C., and Parhi. K. K. (2007), âÃâ¬ÃËLow-cost parallel FIR structures with 2-stage parallelism,âÃâ¬Ãâ¢IEEE Transactions on Circuits Systems I, Reg. Papers, vol. 54, no. 2, pp. 280âÃâ¬Ãâ290.
- Chung, J.G., and Parhi, K.K. (2008), âÃâ¬ÃËFrequency-spectrum- based low-area low-power parallel FIR filter design,âÃâ¬Ãâ¢EURASIP J. Appl. SignalProcess.
- Lin, I.S., and Mitra, S.K (1996), âÃâ¬ÃËOverlapped block digital filtering,âÃâ¬Ã IEEE Transactions on Circuits Systems II, Analog Digital Signal Processing, vol.43, no. 8,pp. 586âÃâ¬Ãâ596.
- Mou, Z.J., and Duhamel, P. (1991), âÃâ¬ÃËShort-length FIR filters and their use in fast non-recursive filtering,âÃâ¬Ãâ¢IEEE Transactions on Signal Processing, vol. 39, no.6, pp.1322âÃâ¬Ãâ 1332.
- Parker, D.A., and Parhi, K.K.(1997), âÃâ¬ÃËLow-area/power parallel FIR digital filter implementations,âÃâ¬Ã⢠J. VLSI Signal Processing andSystems, vol. 17, no. 1, pp. 75âÃâ¬Ãâ92.
- Parhi, K.K. (1999), VLSI Digital Signal Processing Systems: Design and Implementation. New York.
- Yu-Chi Tsao and Ken Choi ,âÃâ¬ÃËArea-Efficient Parallel FIR Digital Filter Structures for Symmetric Convolutions based on Fast FIR Algorithm,âÃâ¬Ã⢠IEEE Transactions.
|