ISSN: 2320-2459
ISSN: 2320-2459
Gyan Prakash*
Amity School of Engineering and Technology, Amity University, Lucknow, India
Received Date: 13/07/2016; Accepted Date: 27/08/2016; Published Date: 29/08/2016
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
In this communication, electric field emission of electrons from negatively charged cylindrical particles in the regime of nonlinear screening has been discussed. Using the suitable representation of the nonlinear screening by Gurevich and the matrix method, the tunnelling probability of an electron through the potential energy barrier around the charged cylindrical particle has been evaluated as a function of its radial energy; and the corresponding values of the current density have also been calculated. The note completes with the discussion of numerical results. This investigation is useful in dusty plasma and laboratory in case of metallic wires and nanotubes.
Nonlinear screening, Tunnelling effect, Dusty plasma, Electron emission
Tunneling phenomena is most interesting phenomena which is much widely discussed in a variety of areas of physics. It has been pointed out by Mendis et al. [1], Mendis [2], Shukla [3], Shukla and Mamun [4] and Fortov et al. [5] that there are many situations in space and laboratory, where the large negative charge and small radius of the dust particles cause a sufficiently large electric field at the surface, which is enough for significant field emission of electrons to occur from the particle. The electric field emission of the electrons is the dominant process of electron emission in the absence of photoelectric or thermionic emission of electrons from the surface of the particles. It has been specifically pointed by Mendis et al. [1] and Mendis [2] that the electric field emission of electrons from the dust particles should be taken into account in electron/ion kinetics in dusty plasma. Sodha et al. [6] have recently formulated a quantitative theory and concluded that in some situations the incorporation of the electric field emission of the electrons in the formulation has significant effect on the electron/ion kinetics and the charging of the dust particles.
Recently, Sodha and Dixit [7] have made a comparison of the results of the popular Fowler [8] and Fowler and Nordheim [9] theory for the tunneling probability of an electron with those, based on exact solution [10] of the Schrodinger’s equation. It was pointed out [7] that the results of the popular theory [8,9] are at considerable difference with those based on the exact [10] theory; further the formulation of Ghatak et al. [11] and Roy et al. [12] gives almost exact values of the tunneling coefficient for symmetric potentials.
In most of studies (e.g. Shukla and Mamun [4]), the electrical field emission from curved surfaces has been calculated from the expression given by Fowler and Nordheim [9] for plane surfaces and putting the values of the electric field, as that at the curved surface. It is well known that the electric field around a curved surface is far from being uniform and hence it is not appropriate to use the expression of Fowler and Nordheim [9], based on the assumption of a uniform electric field. Besides as pointed out in the preceding paragraph this expression is a poor approximation, even for a plane surface.
Sodha and Kaw [13] and Sodha and Dubey [14] obtained expressions for the tunneling probability and field emission current density from spherical [13] and cylindrical [14] surfaces by solving Schrodinger’s equation, corresponding to appropriate expression for the potential energy of the electron, using the JWKB approximation. Dubey [15] made a similar analysis for the spherical surface, taking into account the image force on the electron. Sodha et al. [16] and Sodha and Dixit [17] have recently investigated the electric field emission from spherical [16] and cylindrical [18] surfaces, using the formalism of Ghatak et al. [11] and Roy et al. [12] ; the screening of the particle by the electrons, ion, and other particles was neglected in these investigations. Sodha and Dixit [19] have also studied the effect of Debye shielding (linear screening) on electric field emission from spherical and cylindrical surfaces and found that screening increases the tunneling probability.
Tsytovich et al. [18] have studied the screening of the charge on the particle, which is an important parameter in the evaluation of the tunneling probability. The nature of screening [18] is determined by the parameter
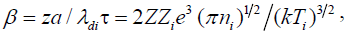 (1)
(1)
Where
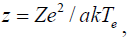
is the radius of the particles,
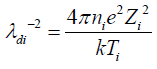 is the ionic Debye radius,
is the ionic Debye radius,
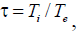
Ze is the charge on the particle,
e is the electronic charge,
k is the Boltzmann’s constant,
ni is the ion density,
eZi is the ionic charge,
Ti is the ion temperature,
and Te is the electron temperature,
In general the potential energy of an electron around a long cylindrical particle with charge –Ze per unit length and radius a is given by
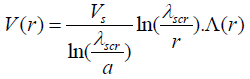 for r > a (2a)
for r > a (2a)
and 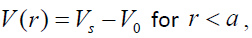 (2b)
(2b)
where 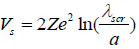 is the potential energy of an electron at the surface of the particle.
is the potential energy of an electron at the surface of the particle.
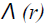 is a function of r, distance from the axis of the cylindrical particle, characterizing the screening of the charge on the particle and V0 is the surface energy barrier.
is a function of r, distance from the axis of the cylindrical particle, characterizing the screening of the charge on the particle and V0 is the surface energy barrier.
When 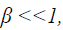 the screening is linear and the screening parameter Λ(r) is given by [18]
the screening is linear and the screening parameter Λ(r) is given by [18]
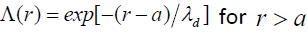 (3)
(3)
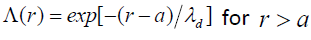
where
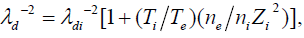
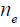 is the electron density and λd is the usual Debye radius in the plasma.
is the electron density and λd is the usual Debye radius in the plasma.
When 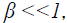 the screening corresponding to Gurevich screening potential is nonlinear and the screening parameter
the screening corresponding to Gurevich screening potential is nonlinear and the screening parameter 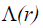 is given by [18]
is given by [18]
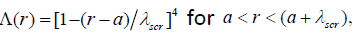 (4a)
(4a)
and
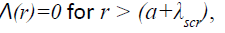 (4b)
(4b)
where
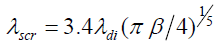
The electric field emission of electrons from the surface of spherical and cylindrical particles has been discussed by Sodha and Dixit [18] for the case of linear screening (β <<1), when the screening is well represented by Eq.(3). The electric field emission from the surface of spherical particles in the region of nonlinear screening has been investigated by Gyan Prakash [19].
In this paper the author has evaluated the tunneling probability (for the electrons with energy more than surface energy barrier (εr (=Er/V0)>1) and the electric field emission current from a negatively charged cylindrical particle for the case, when the screening is nonlinear (β <<1) and represented by Eqs.(4a) and (4b).
Using Eqs. (4a), (4b), (2a) and (2b) the potential energy of an electron is given by
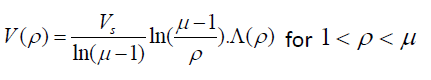 (5a)
(5a)
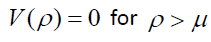 (5b)
(5b)
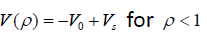 (5c)
(5c)
where
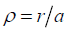
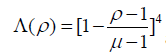 and
and 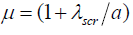
Substituting for V(r) from Eq.(2b), Schrödinger’s equation for an electron inside the particle ( r < a ) may be expressed as
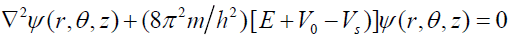 (5d)
(5d)
Where m and E are the mass and total energy of the electron and h is Planck’s constant.
Putting
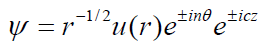 (5e)
(5e)
Where n and c can be interpreted in term of Pθ and PZ (the θ and Z components of linear momentum) as suggested by Sodha and Kaw [13] and Sodha and Dubey [14].
Using Eq.(5e), the equation (Eq.(5d)) reduces to
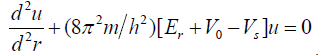
Following earlier workers [13-16,19] the term 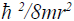 can be neglected as compared to the other energy terms. Er is the radial energy of the electron, the above equation reduces to
can be neglected as compared to the other energy terms. Er is the radial energy of the electron, the above equation reduces to
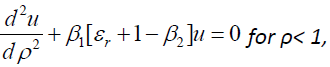 (6a)
(6a)
where
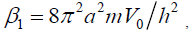
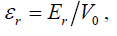
and 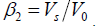
Similarly, for regions 1 < ρ < μ and ρ > μ Schrodinger’s equation may be written using Eqs.(5a) and (5b), one obtains
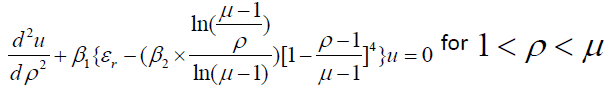 (6b)
(6b)
and 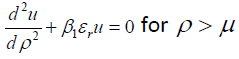 (6c)
(6c)
Using the analytical solution of Eqs.(6a) and (6c) and numerical solution of Eq.(6b) by the well-known matrix method and matching u and 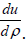 at ρ=1 and μ, the tunneling probability of an electron T(εr) has been evaluated as a function of εr. Details of this approach may in addition to other places be seen in the book by Ghatak and Loknathan [10].
at ρ=1 and μ, the tunneling probability of an electron T(εr) has been evaluated as a function of εr. Details of this approach may in addition to other places be seen in the book by Ghatak and Loknathan [10].
The computations made by the Sodha and Dixit [7] for a plane surface indicate that there is no significant dependence of the current density on the temperature of the metal at least when kT/EF < 10-3. Hence in the present investigation only the case T=0K is considered; in this case the current density is given by [16,19].
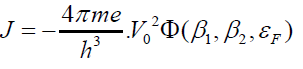 (7)
(7)
where 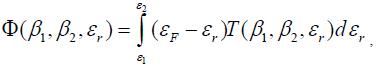
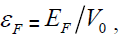
EF is the Fermi energy of the metal and ε1 and ε2 are the limits of εr of electrons taking part in the field emission ; these are
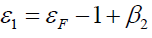 and
and 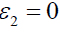
Figure 1 displays the dependence of the tunneling probability T(εr) on the radial energy εr of the electron. It can be seen that the tunneling probability increases with increasing εr and decreasing value of μ (corresponding more intense screening); this is because the width of the energy barrier decreases with increasing εr and decreasing μ. This is also clear from the Figure 1 that energy of the electron is increasing and reaching the surface barrier or beyond, the tunneling probability T(εr) is tending towards the unity. Figure 2 shows the dependence of T(εr) on εr for different values of β2=Vs/V0. It is seen that T(εr) increases with increasing εr and decreasing β2.This is due to the fact for any value of εr, the width of the energy barrier is larger for higher values of β2 (=Vs/V0 ). Figure 3 illustrates that T(εr) increases with decreasing β1 (α V0). This is again because for a given value of εr and β2 (=Vs/V0 ), the width of the energy barrier decreases with decreasing β1 (α V0). Finally Figure 4 shows that the field emission current increases with increasing β2 (=Vs/V0 ) and decreasing μ ( increasing screening). This is a consequence of the dependence of T(εr) on εr and ε1 on β2 and μ, as displayed by Figures 1-3. Eq.(7) along with the computed values of Ãâ°Ã¸ is an essential input for the investigation of the kinetics of complex plasmas, when the role of electric field emission of electrons by the particle is significant.