ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| M.S. Chauhan1 Dheeraj Aheere2 Bharat Singh3 Asst. Prof. Rajabhoj Govt. College,Mandideep Dist. , Raisen (M. P. ) India1 Research Scholar, Vikram University, Ujjain (M. P) India2 Reader, SOC & E IPS Academy Indore (M. P. ) India3 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper ,we generalize fuzzy metric space in term of fixed point theorem in modified Intuitionistic fuzzy metric space using weakly compatible mapping along with property (CLRS) and (CLRT).
Keywords |
| fixed point, intuitionistic fuzzy metric, implicit relation, compatibility |
INTRODUCTION |
| Aanassov[2] Introduction in studied the concept of Intuitionistic fuzzy set as a noted generalization of fuzzy set which has inspired intense research activity around this newly introduced notion. Recently Park[7] using the idea of Intuitionistic fuzzy sets. Defined Intuitionistic fuzzy metric spaces as a generalization of fuzzy metric spaces due to George and Veeramani[4] and also proved some basic results which include Baire’s theorem and uniform limit theorem besides some other core results. Afterthat ,Saadati and Park[8] defined precompact sets in Intuitionistic fuzzy metric spaces and proved that any subset of an Intuitionistic fuzzy metric space is compact if and only if it is precompact and complete.They also defined topologically complete Intuitionistic fuzzy metrizable space and proved that any Gïÿýïÿý set in a complete Intuitionistic fuzzy metric space is a topologically complete Intuitionistic fuzzy metrizable space and vice versa.George and veeramani [11] modified the concept of fuzzy metric space due to Kramosi and Michalek [6] and defined a Hansdorff topology on modified fuzzy metric space which often used In current researches. Grabiee [5] extended classical fixed point theorems of Banach and Edelstein to complete and compact fuzzy metric spaces respectively. The theory of fuzzy sets was initiated by Zadeh [13]. In the last four decades, like all other aspects of Mathematics various authors have introduced the concept of fuzzy metric in several ways. |
II. PREMILIRIES |
 |
| for all x,y ,z,x’ and y’∈L*. |
 |
 |
 |
 |
III. MAIN RESULTS |
 |
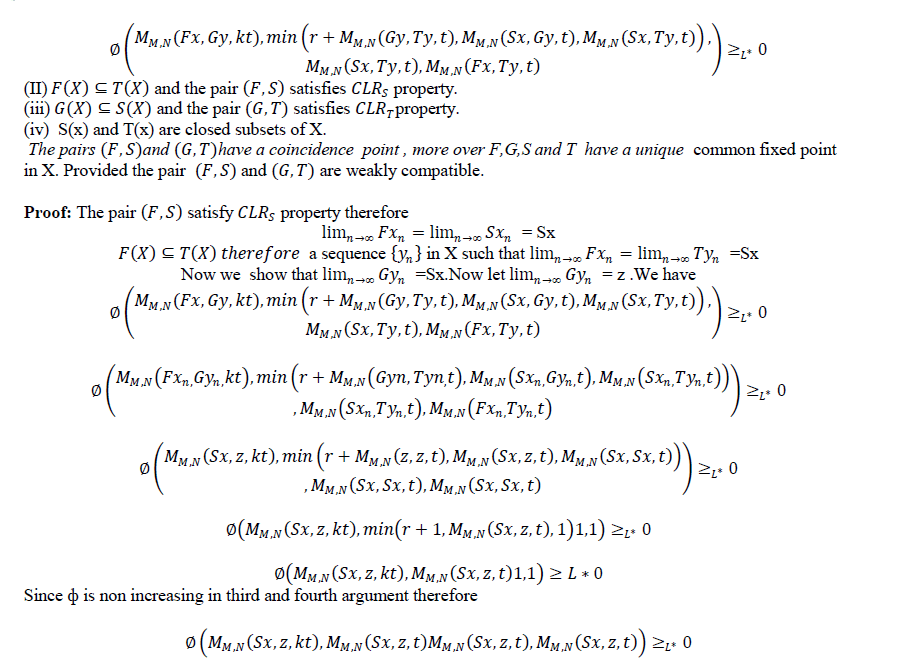 |
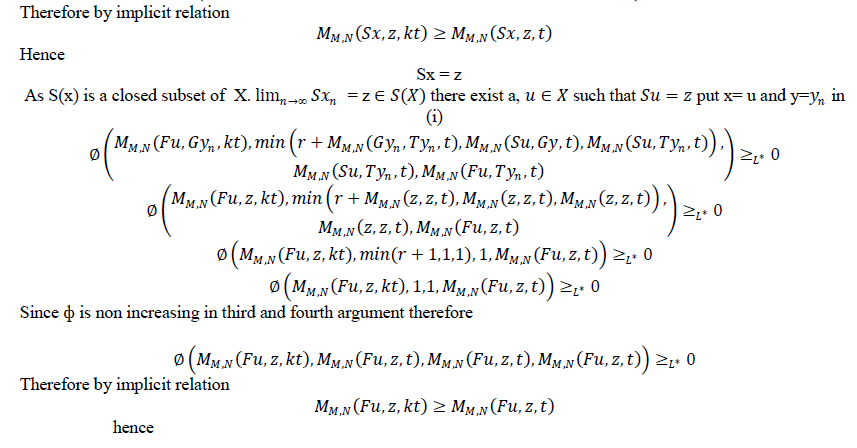 |
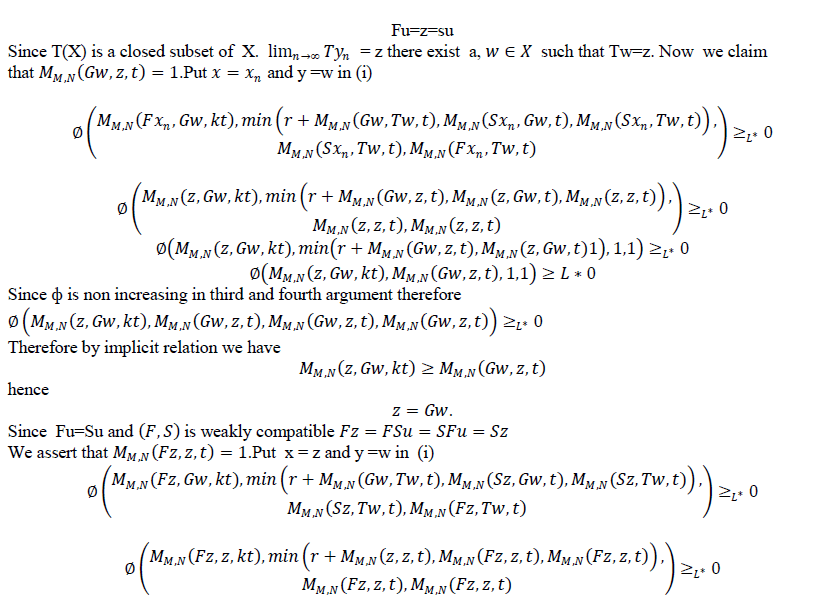 |
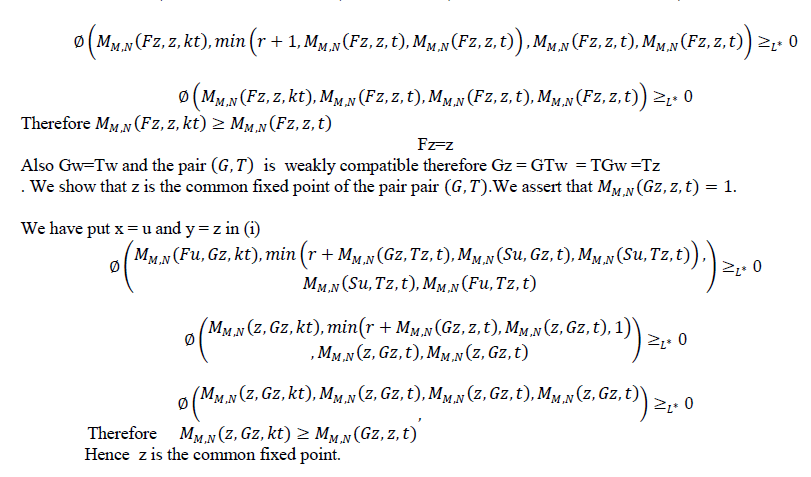 |
| Theorem 3.2 Let f,g,S and T be self mappings of a modified IFMS (X,M,T) satisfying the conditions(i-iv) of theorem 3.1.suppose that |
| (v) S(X) (orT(X)) is a closed subset of X. |
| Then the pairs (f,S) and (g,T) have a coincidence point. Moreover, f,g,S and T have a unique common fixed point in X provided that the pairs (f,S) and (g,T) are weakly compatible. |
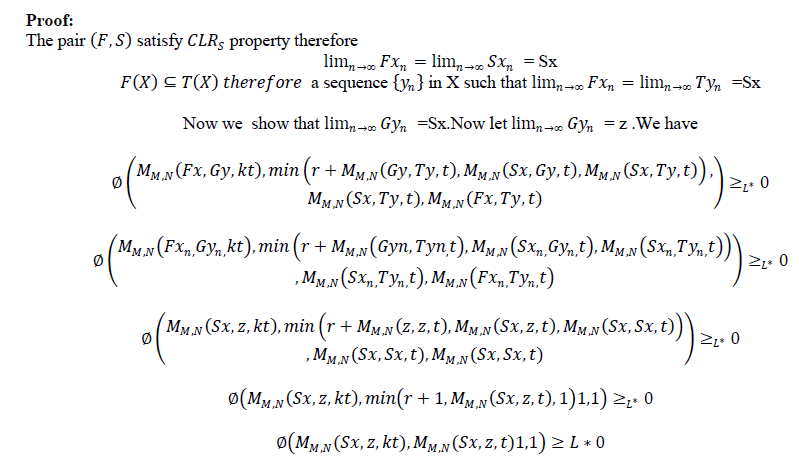 |
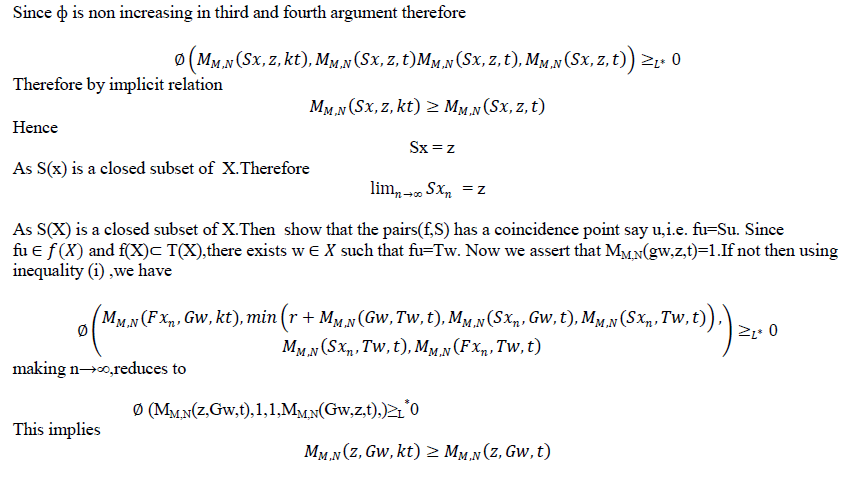 |
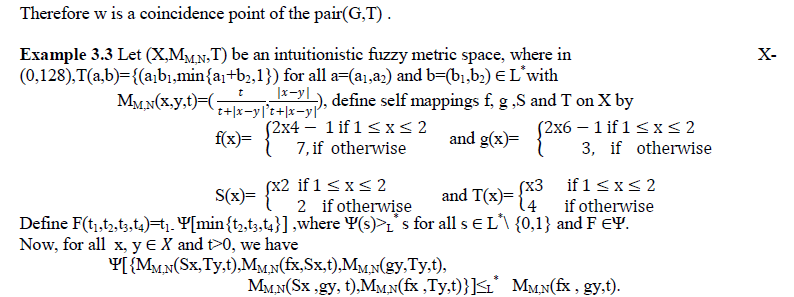 |
| Which demonstrates the verification of the esteemed implicit function. |
References |
|