International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Fixed Points of Different Contractive Type Mappings on Tensor Product Spaces

Dipankar Das1, NilakshiGoswami2
  1. Research Scholar, Department of Mathematics, Gauhati University, Guwahati-781014, Assam, India
  2. Assistant Professor, Department of Mathematics, Gauhati University, Guwahati-781014, Assam, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In this paper, we derive some fixed point theorems in the projective tensor product ) of two Banach spaces X and Y. Using two mappings and , we construct a self-mapping T on . Taking and as different contractive type mappings, we study the characteristics of the mapping T and the existence and the uniqueness of the fixed point of T in the closed unit ball of . The converse of this result is also discussed here.

Keywords
projective tensor product, contractive type mappings, asymptotically regular property

I. INTRODUCTION
image

II. MAIN RESULTS
The following Lemma plays an important role in proving our main results.
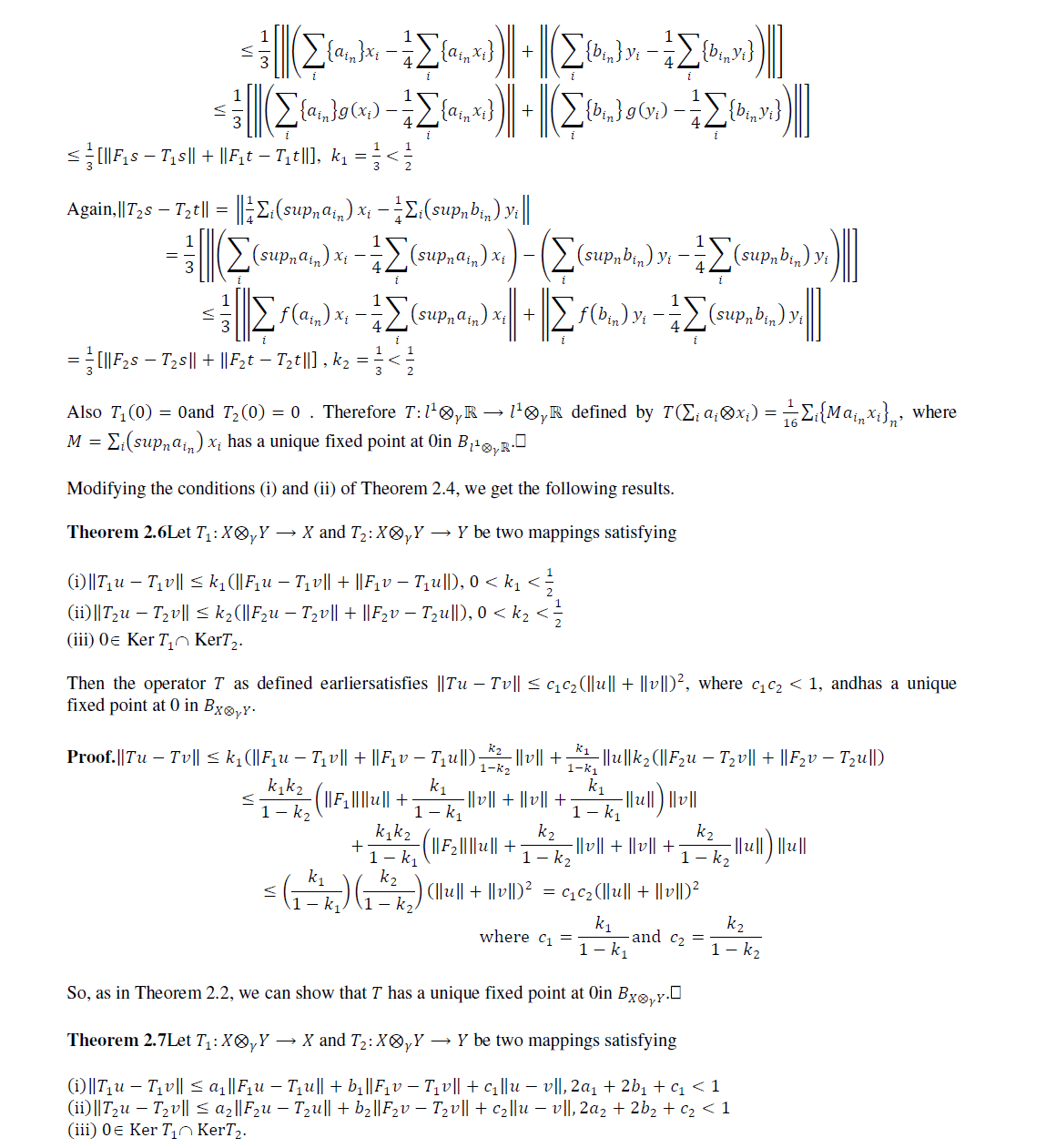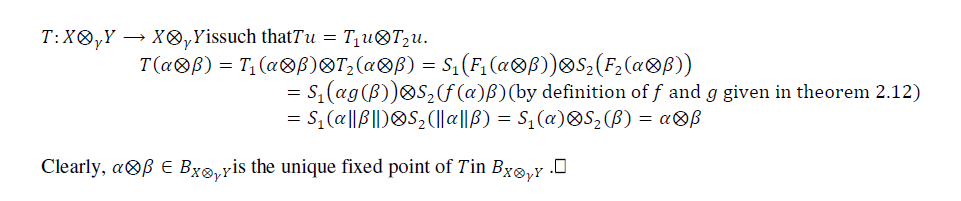image
image
image
image
image
image
image

III. CONCLUSION
image

References
  1. Ya.I. Alber, S. Guerre-Delabriere, “Principles of weakly contractive maps inHilbertspaces,” Operator Theory Advances and Appl., vol.98, pp. 7– 22, 1997 BirkhäuserVerlag Basel/Switzerland.
  2. S. Banach, “Sur Les operations Dans Les Ensembles Abstraits Et Leur Application Aux Equations Untegrales, ”Fund. Math., vol.3 , pp.,133-181,1922.
  3. D. Boyd and J. Wong, “On non-linear Contractions”, Proc. Amer. Math. Soc. vol.20 , pp. ,456-464,1969
  4. F.E. Browder, and W.V. Petrysyn. “The Solution by Iteration of Nonlinear Functional Equation in Banach Spaces,” Bull. Amer. Math. Soc. vol.72, pp ,571-576,1966
  5. S. K. Chatterjea, “Fixed Point Theorems,” C. R. Acad. Bulgare Sci., vol.25 , pp.727-730, 1972
  6. Lj.B. Ćirić, “A Generalization of Banach’s Contraction Principle,” Proc. Amer. Math. Soc.vol.45 , pp.267-273 1947,
  7. R. Kannan, “Some Results on Fixed Points” Bull. Cal. Math. Soc.,vol.60 , pp.71-76,1968 .
  8. M. Saha, D. Dey, “Fixed Point of Expansive Mapping in a Banach Space,” International J. of Math. Sci. and Engg.Appls., vol.4 , no. , pp. 355-362,2010 .
  9. M. Saha, D. Dey. and A. Ganguly, “A Generalization of Fixed Point Theorems in a 2-metric Space”, General Mathematics, Romania vol.19 , no.1,87-98,2011.
  10. Raymond A. Ryan, Introduction to Tensor Product of Banach Spaces,London,Springer -Verlag,2002.
  11. S. Reich, “Some Remarks Concerning Contractive Mapping,” Canad. Math. Bull.,vol.4 , no.1 pp. 121-124 ,1971
  12. B.E. Rhoades, “Some theorems on weakly contractive maps,” Nonlinear Analysis,Vol. 47, pp. 2683–2693, 2001.