ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
N Narasimhulu1, T Sikindar babu2 and M Shiva kumar3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Much of the research has been focused on developing the optimization techniques, varying from classical to non traditional soft computing techniques, to solve the distribution system planning problem. Most of the methods preserve the distinctions and niceties, but dependent on complex search algorithm with a lot of convergence related issues that require more time to reach a firm conclusion at planning stage. This paper proposes a simple direct solution that significantly reduces the inherent difficulties of finding the solution and ensures optimum solution at the same time. Moreover, the concept of optimality is effectively used to make the proposed technique more computationally efficient and useful. The effectiveness of the developed planning technique has been verified with different test cases. The motivation behind the work is to reduce the complexities associated with The methodology of distribution system planning without compromising the optimality of the Solution. Therefore, a comprehensive approach of radial distribution planning has been developed involving all the associated parameters and possible constraints
Keywords |
| Distribution system planning, direct solution approach, principle of optimality, load flow analysis |
INTRODUCTION |
| The main objective of the distribution system planning is to determine the substation location, size and its service area, number of feeders and their routes. A planning cost and its constraints are accordingly formulated to obtain the solution. Mathematically, the problem is nonlinear, non-differentiable, and combinatorial in nature with a large number of discrete and continuous variables. The problem is solved in different time frames as either single or multiple horizons employing the right strategy. Various mathematical programming techniques, such as integer programming, mixed integer programming, transportation, transshipment, and branch and bound methods have been applied to the problem of feeder routing optimization. Among the classical solution methods, the most preferred method is mixed integer linear programming (MILP). The MILP is a multistage solution technique where the nonlinear problem is transformed to linear problem without any integer restriction and is solved by employing any linear programming technique. The variables are then modified by the commonly used branch and bound method. These models are difficult to solve and the solution time increases for such problem like distribution system planning, where large number of discrete variables are present. Evidently good initial guess of the variables can reduce the solution time. The planning of secondary distribution circuits is also approached as a mixed integer nonlinear programming problem (MINLP). |
| A dedicated Evolutionary Algorithm (EA) is proposed to solve this problem. Fletcher and K. Strunz proposed a mathematical model for optimal expansion of both primary and secondary distribution systems for each period of the planning horizon. That model is solved using a classical optimization technique based on a direct derivative gradient search method. Antonio Marcos Cossietal. Formulated the secondary distribution circuit expansion as a MINLP and Tapu search method is used to solve the problem. Recently, some works using genetic algorithms (GAs), Simulated Annealing, and Ant Colony based techniques for planning of distribution system have been reported. Besides obtaining higher chance to achieve better result, nonlinearity of the cost function, real and integer variables, nonlinear constraint scan easily be incorporated in formulation while using these optimization techniques. The potential of the GA is shown in comparison with the classical technique. This is true that in GA, the length of binary strings representing the integer variables becomes high even for medium size network and therefore, this leads to extremely large number of unfeasible solutions. Simulated Annealing technique is applied to solve the problem. Author in this Simulated Annealing based approach generates initial solution by steepest descent method. Then the initial network is modified by including a new branch that is selected randomly. Subsequently the newly formed mesh is opened by removing a branch selected by a random selection process again. Each of the above moves follows a full load flow to check the effect of inclusion of new branch in the network. In the Ant Colony based method, the optimal network is obtained by movement of ants from one node to another node where each move is decided by magnitude of pheromone accumulated in different paths and a heuristic guide function. A number of parameters are required to tune and 1000 runs of the algorithm are required for proper tuning of parameters, as reported by Gomez et al. based method, the optimal network is obtained by movement of ants from one node to another node where each move is decided by magnitude of pheromone accumulated in different paths and a heuristic guide function. A number of parameters are required to tune and 1000 runs of the algorithm are required for proper tuning of parameters, as reported by Gomez et al.. A different approach based on branch-exchange techniques have been applied in distribution system planning. |
| The motivation behind the work is to reduce the complexities associated with the methodology of distribution system planning without compromising the optimality of the solution. Therefore, a comprehensive approach of radial distribution planning has been developed involving all the associated parameters and possible constraints. |
 |
OBJECTIVE FUNCTION |
| Distribution system planning analysis is designed to minimize the LOSSES FEEDER LENGTH becomes high for a radial path when there is no power available in entire route for any interruption. In the radial networks, there is no alternative supply route and the outage of a branch interrupts the delivery to all the consumers supplied through this branch |
| The constraints to be satisfied are: |
| A) Conservation of power flow: IP=D where P=(P1,P2,P3…PN) is the vector of power flow, and D=(D1,D2,D3,DN ) is the vector of power demand at each of N nodes, and I is node element incidence matrix. |
| B) Capacity constraint is the vector of capacity limits. Maximum current limit in case of feeder, maximum practical kVA rating in case of substation. |
| C) Radiality constraint. |
| D) Voltage drop constraint |
 |
FORMATION OF OPTIMUM RADIAL NETWORK |
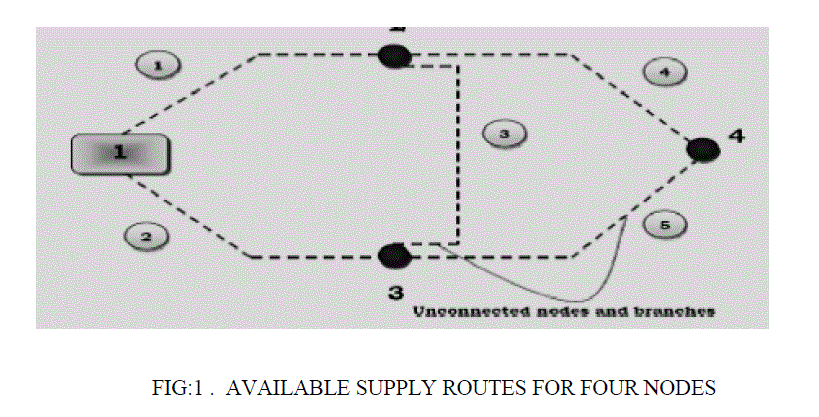
| The proposed direct solution technique is basically based on searching the optimum path for energizing a node among all the possible paths. There may be several possible radial paths to reach a node, from a substation. The path among all the radial paths for feeding a particular node will be the optimum path for the node. This essentially is an iterative search technique where the minimum path for a node is searched in iteration. In the beginning of the search, all possible radial paths for each node have been traced out. As in Fig. 1, 1-2-3-4 is one of the four different available radial paths to feed a node 4. Forward/ backward load flow technique is then applied to find the energy loss. Subsequently planning is calculated for each of the four radial paths according to routing optimization. There are basically two problems to be solved. The first one involves tracing out the radial paths from large number of possible connections and the second one is computing the cost of calculation for large number of radial paths. An easy step by step algorithm is proposed to solve the first problem. The concept of the principle of optimality is used for the second problem. The principle of optimality theorem states that from any point on an optimal trajectory, the remaining trajectory is optimal for the corresponding problem initiated at that point. There may be more than one node on any optimum path. Once an optimal path is found for any node, the theorem states that the parts of this optimal path will be the optimal path for all the nodes which are lying along the trajectory. Therefore, it is not required to carry out searching the optimum radial path for all the nodes separately. As a result, Voltage calculation is required for making decision on limited nodes only. Global solution is ensured by verifying all the possible radial paths to reach a node before deciding the optimum route for individual node. |
ALGORITHM FOR TRACING RADIAL PATH FOR ALL THE NODES |
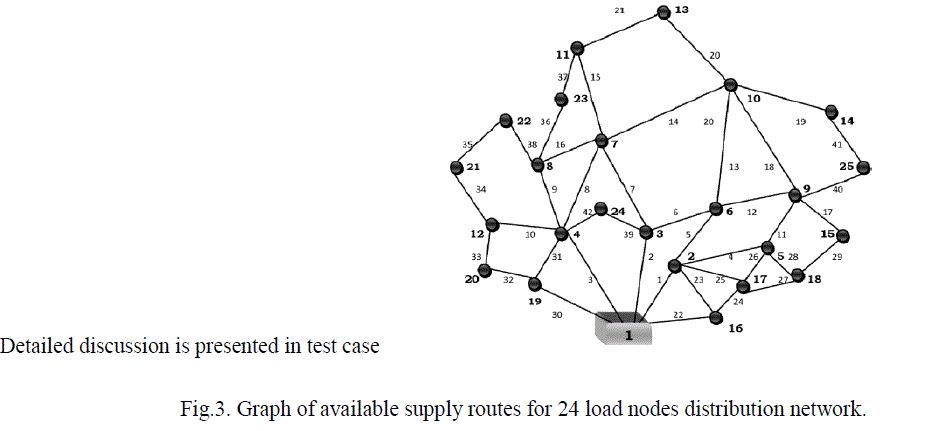
| The radial distribution system is always a directed path, where power is directed from a substation to the load nodes. A directed graph is an ordered pair D = V,A)with V = a set whose elements are called vertices or nodes, and A a set of ordered pair of vertices, called arcs, directed edges or arrows. An arc A=(X, Y) is considered to be directed from x to y, where y is called head and x is called the tail of the arc. Every arc will be a radial path starting from any substation. Let us consider a network as shown in the Fig. 1 with all possible paths to feed the three load nodes (2, 3, 4 ) from substation node 1. The dotted lines represent the probable connections to energize the nodes from the substation node 1. A step by step radial path building algorithm developed to determine all the radial paths is summarized below. |
| STEP 1: |
| Initial arcs with substation This work initiate with development of arc with the load nodes connected directly with substation. Therefore, the number of initial arcs depends on the number of feeders coming out from the substation. In an arc (x, y), x (tail) will be the substation and y (head) will be the set of load nodes that are connected with x. ,Y={y1,y2,…yn} where, y set of load nodes directly connected with substation x. Thus there are n numbers of arcs after first step that can be written as A= {(XY1,)(XY2),(XYn)} Referring to the Fig. 1, we can write A= {(12),(13)} where X=Substation node 1, y=A set consisting of load nodes 2 and 3 which are directly connected with the substation node 1. |
| STEP 2: |
| New arcs by extending load nodes At the next step, load nodes connected with substation node acts as tail (x) of the new arc where in the new head (y) depends on the connectivity with the other nodes. As explained earlier, an arc represents a radial path and therefore a new arc adds only a head at a time with an old arc. While updating an arc, it is to be checked that head does not appear in an existing or old arc. Updating of arcs will be continued till all the possible load nodes are covered. nodes 2 and 3 will now be acting as tails in step 2, to be connected with new heads. From Fig. 1, it is clear that 2 may be connected to 1, 3 or 4. But 1 is already present in initial arcs; therefore 1 will not be appearing in a new arc. With node 2, updated arcs are{(124),(123)} Similarly, with node 3, updated arcs are {(132),(134)} Hence, New updated .A= {(12),(13),(124),(123),(132),(134)}. The continuation of this update will happen till all the four nodes are expanded. Combining all arcs, the final A will be,{(12),(13),(123),(123),(132),(134),(1243),(1234),(1324),(1342)}. |
| STEP 3: |
| Zero padding In this step, set A is converted to equivalent matrix E of specific dimension. In order to maintain same number of elements in each row, zero padding is carried out. Hence, the number of zeros to be entered in each row is calculated using , Number of zeros in each row ,Zp= [(n+1)-Nz] Where n=total number of nodes and Nz =non zero element of radial path In matrix form, we can write |
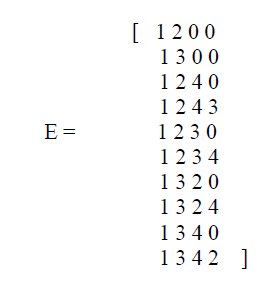 |
| If there is more than one substation, the same steps 1 to 3 will be followed to construct final E matrix for each substation. It is apparent that the last nonzero element in each row of matrix E represents the last load node of its radial path. As in node 2 appears three times as last nonzero nodes, therefore, there are three different possible radial paths to energize node 2, as represented by a matrix in E2 |
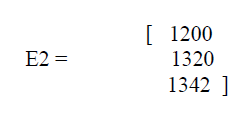 |
| After that, we have to calculate the cost of the each radial paths of matrix, the path is selected as optimum for node 2. |
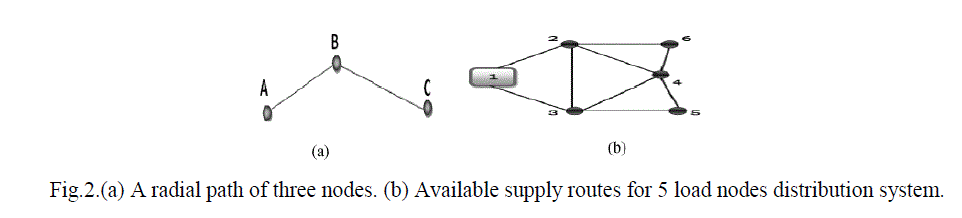 |
Principle of Optimality |
| The number of radial paths before finalizing the route to energize a node .The strategy becomes computationally overburdened considering the total number of paths arising for a given node. Computational complexity can be drastically reduced and consequently the strategy becomes more effective if the theorem of principle of optimality is followed. The theorem is largely concerned with dynamic programming optimization technique which states that: If the best possible path from A to C passes through intermediate point B, then the best possible path from B to C must be the corresponding part of the best path from A to C as in Fig. 2(a). Referring to Fig. 2(b), if 1-2-4-6 is found to be optimal for node 6, then according to optimality theorem there is no need to check the optimal path for nodes 4 and 2 as these nodes are on the optimal trajectory because 1-2-4 and 1-2 are the parts of optimal path 1-2-4-6. Thus this strategy of using principle of optimality reduces searching of optimal paths |
Effective Way of Applying the Technique |
| As per the principle of optimality, separate search is not required to identify the optimal path for a given node, once this node is on the optimal path of any other node. Therefore, to obtain maximum advantage from the principle of optimality theorem, the optimal routing should be started with the terminal nodes that are farthest away from the substation. As per Fig. 4, terminal nodes to be considered are 13, 10, 14, 25, 15, 11, 22, and 21. The identified optimal paths of these terminal nodes are likely to cover most of the other nodes of the system on their paths. Separate search is only required for the nodes which are not covered on the optimal paths identified for the terminal nodes. Therefore, there is no chance of missing the optimum number of main feeders, their routings and routing of their respective laterals. The computational time is also drastically reduced as cost evaluations need to be done for fewer paths. |
 |
 |
SIMULATION RESULTS |
| The feasibility of the developed planning technique has been verified by test cases. |
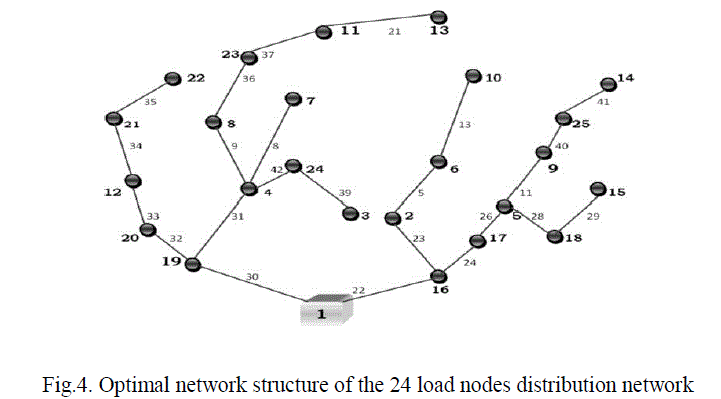 |
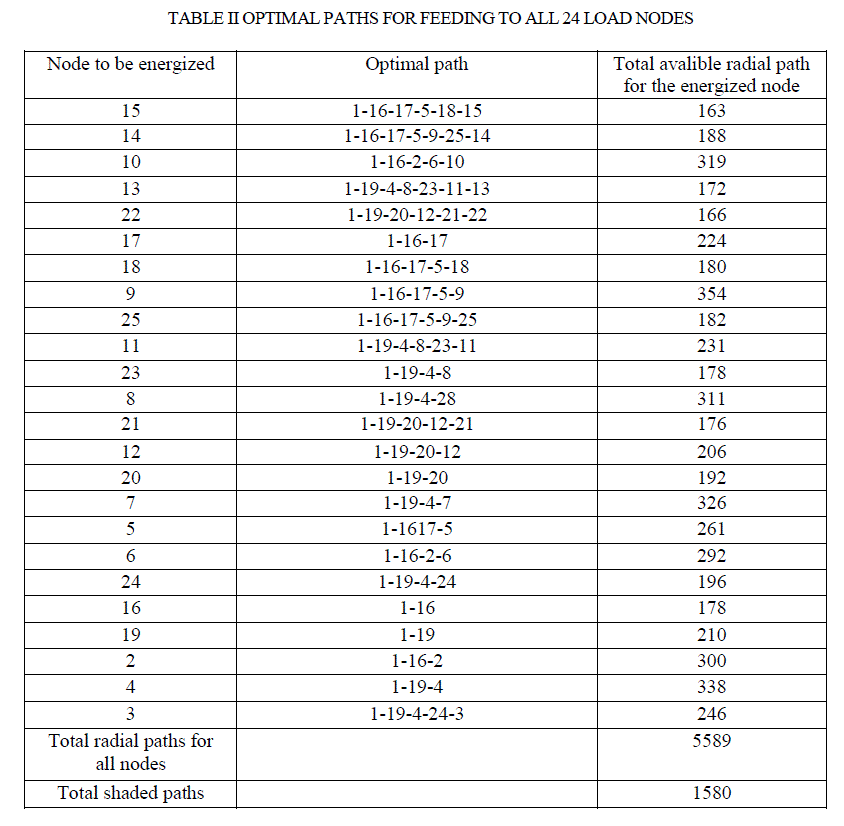
| The distribution planning problem reported has been considered. The system has 25 nodes and 42 available branches for their supply from the substation 35 kV/10.5 kV at node 1, as shown in Fig. 3. Total load in the network is 2.55 MVA. The substation cost has been included with the feeder related data for every outgoing line emanating from substation. As the first step, the matrix âÃâ¬Ãâ¢EâÃâ¬Ãâ as containing all the possible radial paths is framed following the steps of building algorithm. Finally building algorithm generates 5589 total radial possible paths for energizing all nodes as shown in column-3 of Table II. After tracing all the possible radial paths for energizing all nodes, decisions for finding optimal routes are taken for the nodes 13, 10, 14, 25, 15, 11, 22 and 21. At the beginning of the method, any node can be selected but it is recommended to select those nodes first which are farthest from substation to reduce the cost evaluation burden as well as time required. Further search is not required to find the optimal path for any node, once this node gets a place on any optimal trajectory of feeding any other node. Decisions are required for only 7 nodes that are sufficient to cover all the other nodes of the system which is also apparent from Table II. For example, the optimal path for 13 decides the routes of energizing nodes of 19, 4, 8, 3, 11, and 13. As in Table II, all the other loads are lying on at least one optimal trajectory found for terminal nodes except 3 and 7. Therefore the proposed technique is developed on MATLAB R2006b code and the computational time required is only 5 minutes using computer: PC Pentium, 1.98 GHz, and 1 GB of RAM. Total losses occurring in this network amounts to 0.0314 MW Optimal network structure obtained by this method is shown in Fig. 4, which is similar to the network obtained from the reported Simulated Annealing method. |
 |
CONCLUSION |
| This approach builds on simple concept that depends solely on tracking of radial paths and calculating with the paths. An easy step by step building algorithm is proposed to find the radial paths existing in a system. The work has also explored the advantage of theorem of principle of optimality and successfully established a link with radial system planning that makes the process of searching faster and more effective. The proposed technique ensures global optimal solution without being influenced by initial paths as considered in classical techniques or different parameters as required by soft computing techniques for tuning. Along with the routing, the solution of optimal number of substations is also proposed. Radial path building algorithm may be considered a useful tool for typical route planning problem. |
ACKNOWLEDGMENT |
| Our thanks to the experts who have contributed towards development of the template. |
References |
|