ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| SRIDHAR RAJA. D Asst. Professor, Department of electronics & instrumentation, Bharath University |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
The main objective of this project is designing UWB Bandpass filter based on electromagnetic bandgap (EBG) structures .Mainly the focus is on the compactness and performance of the filter design which will be compared with conventional wideband filter .In this three EBG structures are investigated and applied to UWB BPFs. The UC–EBG cell is divided in four sectors with the cross line, while each sector of UC–EBG is similarly split into four sectors in the FUC–EBG cell and third with simple EBG Embedded Multi Mode Resonator.
INDEX TERMS |
| Bandpass filter, electromagnetic bandgap (EBG), ultra wideband (UWB), wideband filter. |
INTRODUCTION |
| The Ultra-wideband (UWB) technology is being reinvented recently with many promising modern applications. In particular, the UWB radio system has been receiving great attention from both academy and industry since the Federal Communications Commission (FCC) release of the frequency band from 3.1 to 10.6 GHz for commercial communication on applications in February 2002. In an UWB system, an UWB band pass filter (BPF) is one of the key passive components to keep the spectrum of the signals to meet the FCC limits, or used in the UWB pulse generation and reshaping. |
| In such a system, an UWB filter is one of the key components, which should exhibit a wide bandwidth with low insertion loss over the whole band. In order to meet the FCC limit, good selectivity at both lower and higher frequency ends and flat group-delay response over the whole band are required. The recent research and development practical applications of EBG structures have improved realizing compact EBG structures filters. |
OVERVIEW OF EBG STRUCTURES |
| Periodic structures are abundant in nature, which have fascinated artists and scientists alike. When they interact with electromagnetic waves, exciting phenomena appear and amazing features result. In particular, characteristics such as frequency stop bands, passbands, and band gaps could be identified. |
| Electromagnetic band gap structures are defined as artificial periodic (or sometimes non-periodic) objects that prevent/assist the propagation of electromagnetic waves in a specified band of frequency for all incident angles and all polarization states. |
| Electromagnetic band-gap (EBG) structures are periodic structures which can prohibit the propagation of electromagnetic wave in certain band of frequency. They can be embedded in the dielectric substrate or etched on the metal layers. The EBG structures are always used to help suppress the surface waves to gain good pass band or stop band. |
| There are two types of EBG structure to be discussed. Firstly is Perforated dielectric and the second one is Metallodielectric structures. Perforated dielectric is defined as effectively suppress unwanted substrate mode. This structure designed by drill periodic holes on dielectric subtracts to introduce another dielectric but in practical, this structure is difficult to implement. Metallodielectric structure is exhibits an attractive reflection phase future where the reflected field change continuously from 180 degrees to -180 degrees versus frequency. |
METHOD OF MOMENTS |
| One of the methods, that provide the full wave analysis for the microstrip band pass filter, is the Method of Moments. In this method, the surface currents are used to model the microstrip filter structure and the volume polarization currents are used to model the fields in the dielectric slab. It has been shown by Newman and Tulyathan [17] how an integral equation is obtained for these unknown currents and using the Method of Moments, these electric field integral equations are converted into matrix equations which can then be solved by various techniques of algebra to provide the result. A brief overview of the Moment Method described by Harrington [18] and [5] is given below. |
| The basic form of the equation to be solved by the Method of Moment is: |
 |
| The basic functions gn must be selected in such a way, that each F(g n) in the above equation can be calculated. The unknown constants an cannot be determined directly because there are N unknowns, but only one equation. One method of finding these constants is the method of weighted residuals. In this method, a set of trial solutions is established with one or more variable parameters. The residuals are a measure of the difference between the trial solution and the true solution. The variable parameters are selected in a way which guarantees a best fit of the trial functions based on the minimization of the residuals. This is done by defining a set of N weighting (or testing) functions {w m} = w1, w2 ...w N in the domain of the operator F . Taking the inner product of these functions, equation (3.15) becomes: |
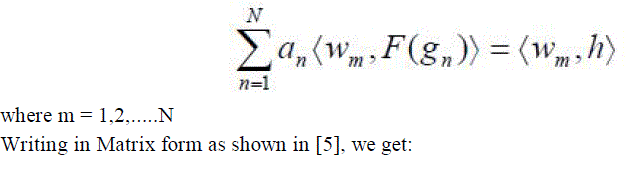 |
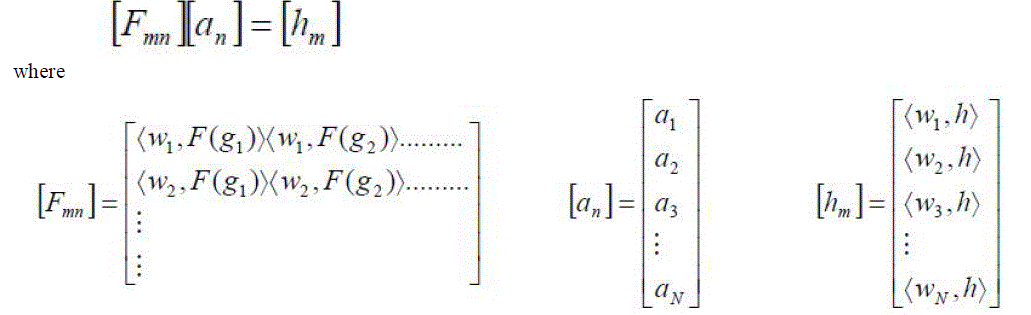 |
| The unknown constants an can now be found using algebraic techniques such as LU decomposition or Gaussian elimination. It must be remembered that the weighting functions must be selected appropriately so that elements of {wn} are not only linearly independent but they also minimize the computations required to evaluate the inner product. One such choice of the weighting functions may be to let the weighting and the basis function be the same, that is wn = gn. This is called as the Galerkin’s Method as described by Kantorovich and Akilov [19]. From the antenna theory point of view, we can write the Electric field integral equation as: |
 |
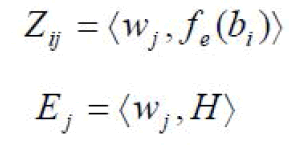 |
| J is the current vector containing the unknown quantities. |
| The vector E contains the known incident field quantities and the terms of the Z matrix are functions of geometry. The unknown coefficients of the induced current are the terms of the J vector. Using any of the algebraic schemes mentioned earlier, these equations can be solved to give the current and then the other parameters such as the scattered electric and magnetic fields can be calculated directly from the induced currents.. The software used for this project work is a Method of Moments simulator. |
FILTER THEORY. |
| Filter are two-port, reciprocal, passive, linear devices which attenuate heavily the unwanted signal frequencies while permitting transmission of unwanted frequencies. The practical filters have a small non-zero attenuation in the pass band and a small signal output in the attenuation or the stop band due to the presence of resistive losses in reactive elements and propagating medium. |
| FILTER PARAMETERS. |
| In filter designing following important parameters are considered. |
| 1. Pass bandwidth |
| 2. Stop band attenuation and frequencies |
| 3. Input and output impedances |
| 4. Return loss |
| 5. Insertion loss |
| 6. Group delay. |
| The most important parameters among the above is the amplitude response given in terms of the insertion loss Vs frequency characteristics. Let Pi be the incident power at the filter input , Pr is the reflected power, PL is the power passed on to the load. The insertion loss of the filter is defined by, |
 |
 |
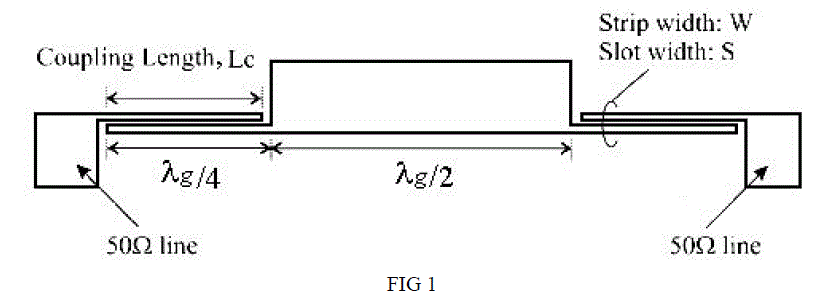 |
| The MMR in the filter generates first and third resonant mode at the edges of the UWB pass band. The parallel-coupled lines are modified to obtain the ultra-wide pass band. This could be done by adjusting the coupling length, Lc. |
| Result obtained Within the UWB passband, the measured insertion and return losses are lower than 2.0 dB and higher than 10.0 dB, respectively. |
| In recent years conventional microstrip band pass filters such as stepped-impedance filters, open-stub filters, semi lumped element filters, end- and parallel-coupled half-wavelength resonator filters, hairpin-line filters, interdigital and combine filters, pseudo combine filters, and stub-line filters are widely used in this parallel-coupled half-wavelength resonator filters are taken in consideration along with EBG structure based filter. |
PROPOSED EBG STRUCTURE. |
| The conventional EBG structure has a wide band-gap and compact nature. The inductor L results from the current flowing through the connecting via. The gap between the conductor edges of two adjacent cells introduces equivalent capacitance C. Thus a two dimensional periodic LC network is realized which results in the frequency band-gap and the center frequency of the band-gap is determined by the formula |
| ω = 1/√LC |
| From above equation it can be seen that in order to achieve an even more compact EBG structure, the equivalent capacitance C and inductance L should be increased. But in the EBG design procedure, if the dielectric material and its thickness have been chosen, the inductance L cannot be altered. Therefore, only the capacitance C can be enlarged . |
| Below fig.2 shows the proposed EBG structures for filter design. |
 |
SIMULATION & RESULTS |
| DESIGN OF PROPOSED UWB FILTERS |
| 3.Foliated UC-EBG filter and result. |
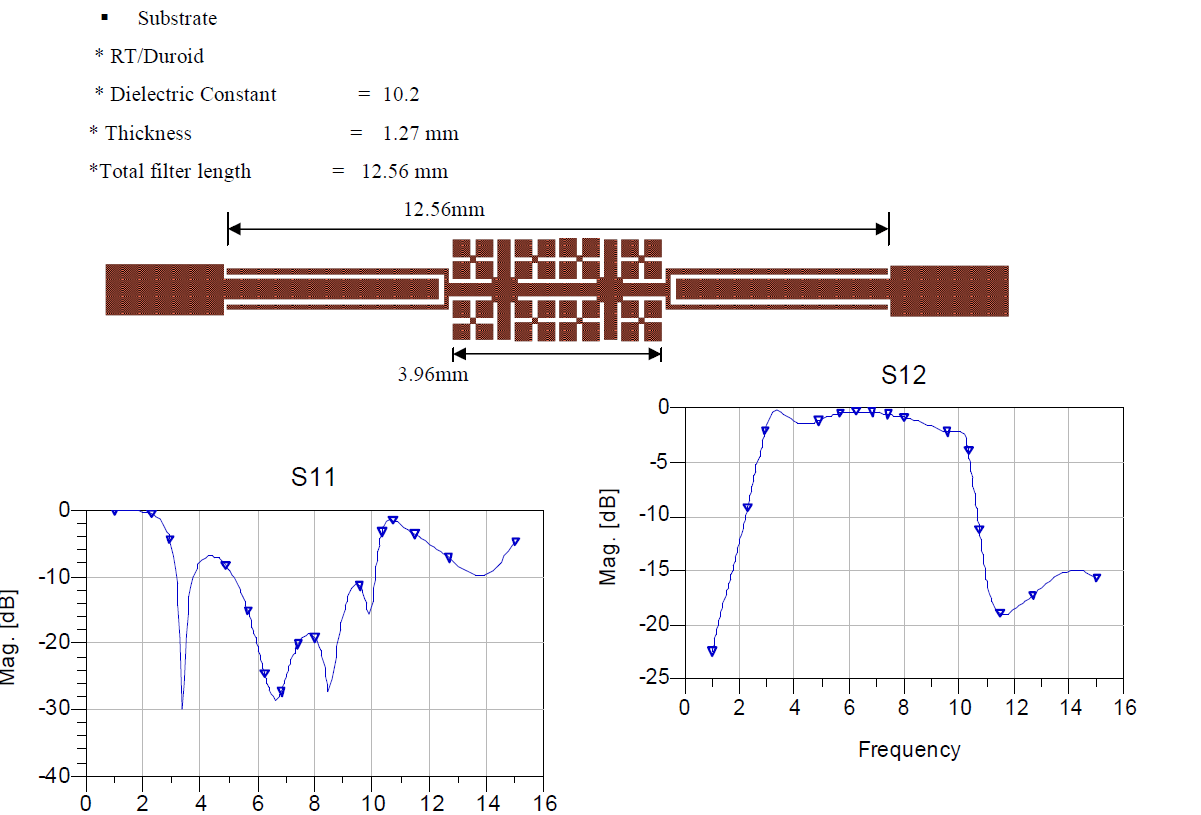 |
| Frequency |
 |
CONCLUSION |
| In this, two UWB BPFs with EBG structures are investigated and simulated.. There results have been compared by simulated using ADS Momentum simulator .The future work is towards improving the good out-of-band performances and other EBG structure to reduce the overall size of the filter. Also to improve the performances of EBG by using defected ground plane. |
References |
|