International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
MenuISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
H. B. Kekre1 and V. R. Lakshmi Gorty2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In this paper, the Kekre’s function is represented in mathematical concept. The Fourier transforms is applied to Kekre’s function and the results are obtained. The graphical representation is shown by MATLAB representing transforms to Kekre’s function. A generalized representation of Kekre’s function is shown in this paper. To all the assigned order N, of the Kekre’s functions, the solutions are displayed for each example. Linearity property using Fourier transforms when applied to Kekre’s function, is proved in the form of a theorem. For any positive arbitrary value, the transform of Kekre function is obtained. At the end of examples, the generalized representation of the Fourier transforms of Kekre’s function is formulated.
Keywords |
| Kekre’s function, Fourier transforms, generalized representation, linearity property. |
INTRODUCTION |
| Burrows and Colwell in [5] highlighted the difficulties which can arise when the Fourier transform of the unit step function is introduced to non-mathematics specialists. In [1] and [2] Kekre and Lakshmi Gorty, represented Mathematical concept of Laplace transforms and inverse Laplace transforms to Kekre’s function. The transforms of the functions in parameter ' s ' has been calculated and are obtained in the form of Kekre’s function. A generalized representation of Kekre’s function is shown in this paper. In [3], author described about the study discrete Fourier transformations of functions of the greatest common divisor and Euler’s totient function. Authors in [6] examine both the mathematics and music background with Fourier series representations of sound waves and found they are related to harmonics and tonal color of instruments. Foliage plant retrieval using polar Fourier Transform, color moments and vein features to retrieve leaf images based on a leaf image has been proposed by Abdul Kadir and others in their paper [7]. The method proved useful to help people in recognizing foliage plants. To understand the different applications the authors in [8] examined the potential of Fourier transform infrared (FT-IR) absorbance spectroscopy to detect biochemical changes in bacterial cells that occur during bacterial growth phases in batch culture. In [9] paper proposes a generalized algorithm to generate discrete wavelet transform from any orthogonal transform. |
| The authors in [10], explained finding a formula that relates the Fourier transform of a radial function on R n with the Fourier transform of the same function defined on R n+2. This formula enabled one to explicitly calculate the Fourier transform of any radial function f(r) in any dimension, provided one knows the Fourier transform of the onedimensional function t→f(|t|) and the two-dimensional function (x 1,x 2)→f(|(x 1,x 2)|). Kekre function is defined as |
 |
PRELIMINARY STUDY |
| Here the order of the Kekre’s function is ‘5’. Then the Kekre’s function can be represented as: |
 |
 |
 |
 |
 |
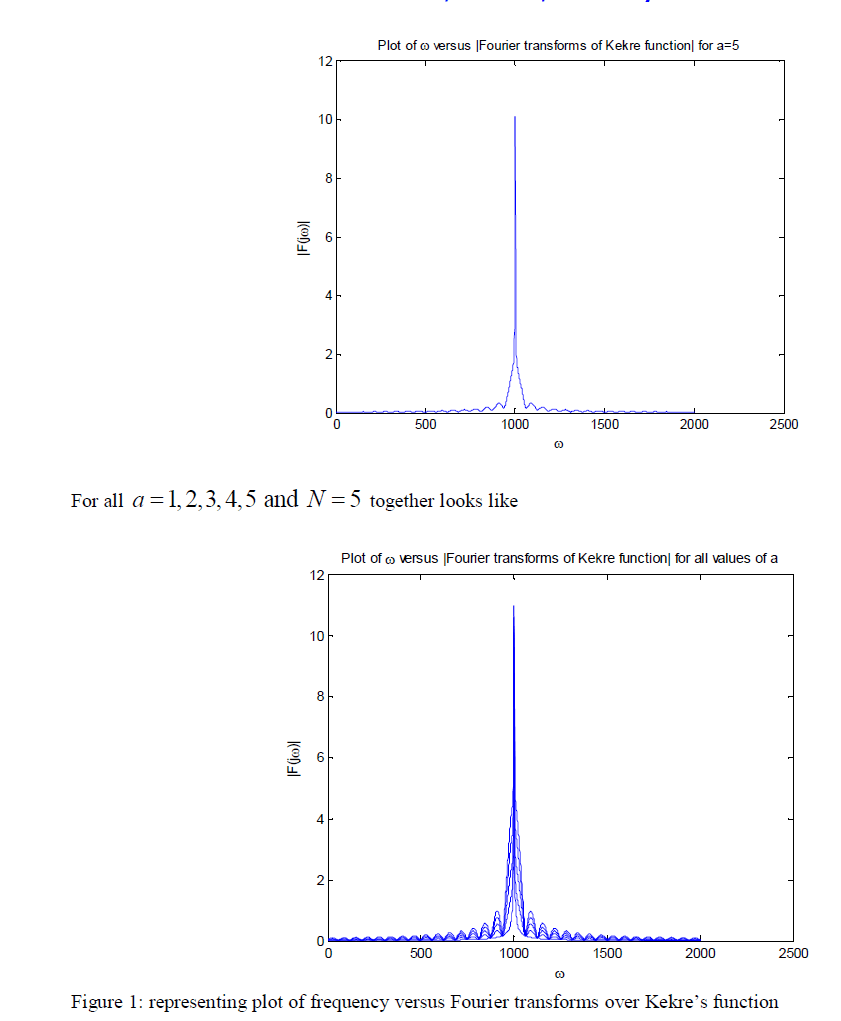CALCULATIONS |
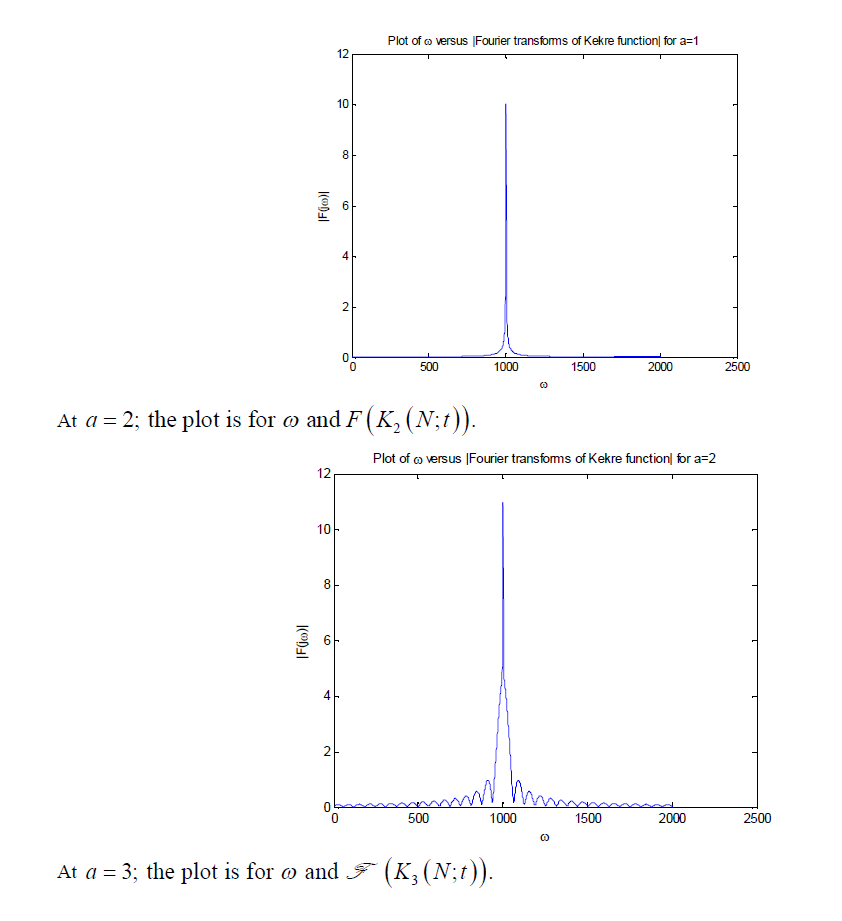
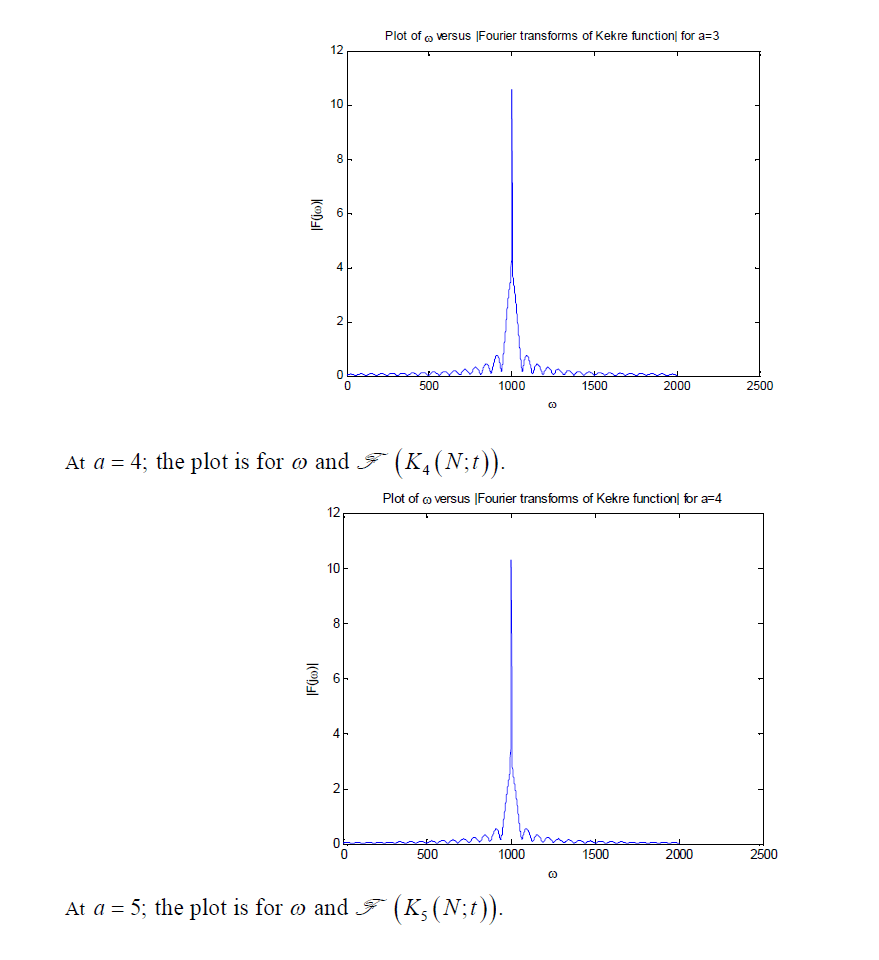
| For a function t Ka (N;t) the Fourier transforms is applied and calculated for N = 5;a = 1,2,3,4,5. On applying Fourier transforms over Kekre’s function from (1), the following results are obtained. |
 |
 |
 |
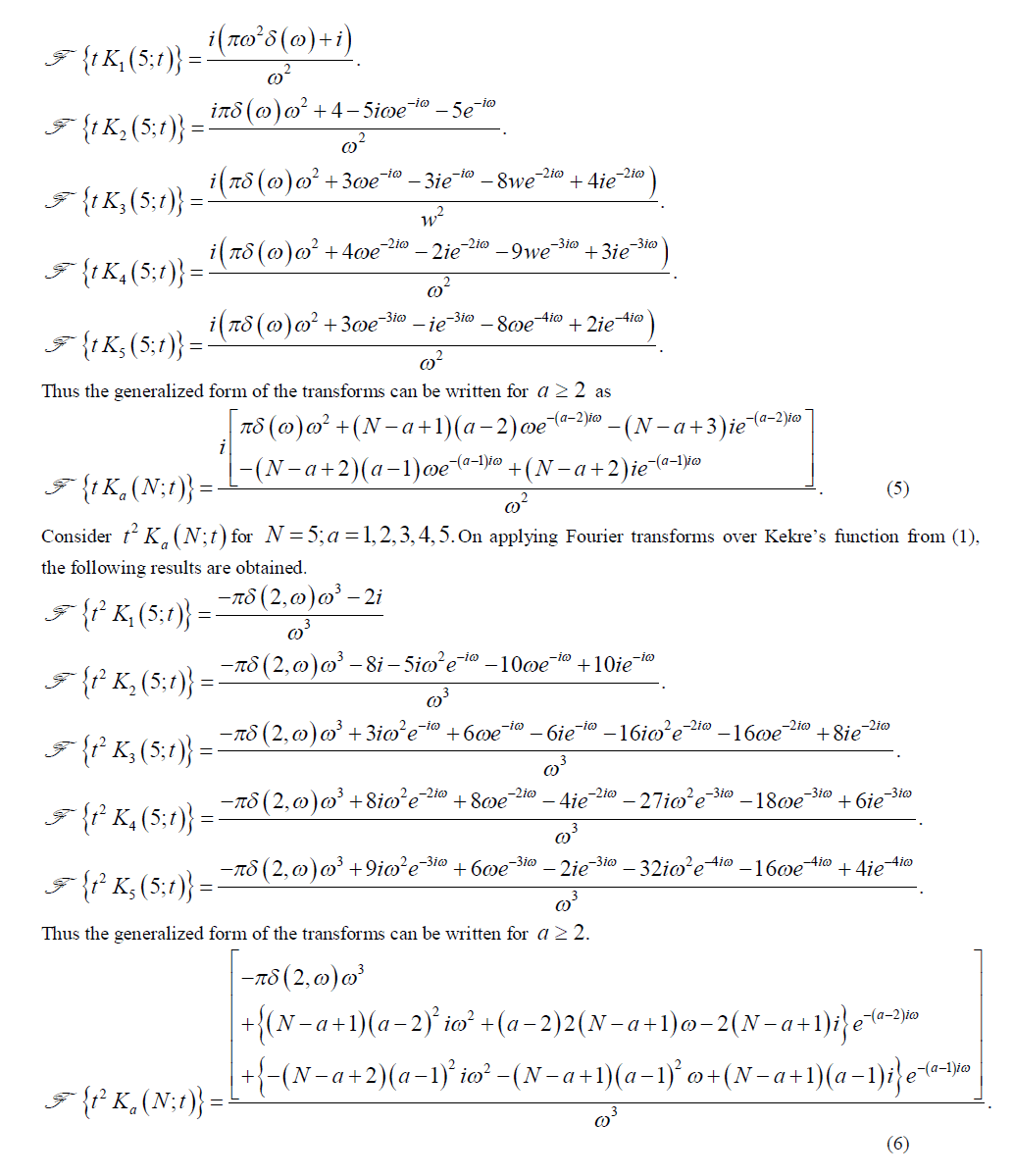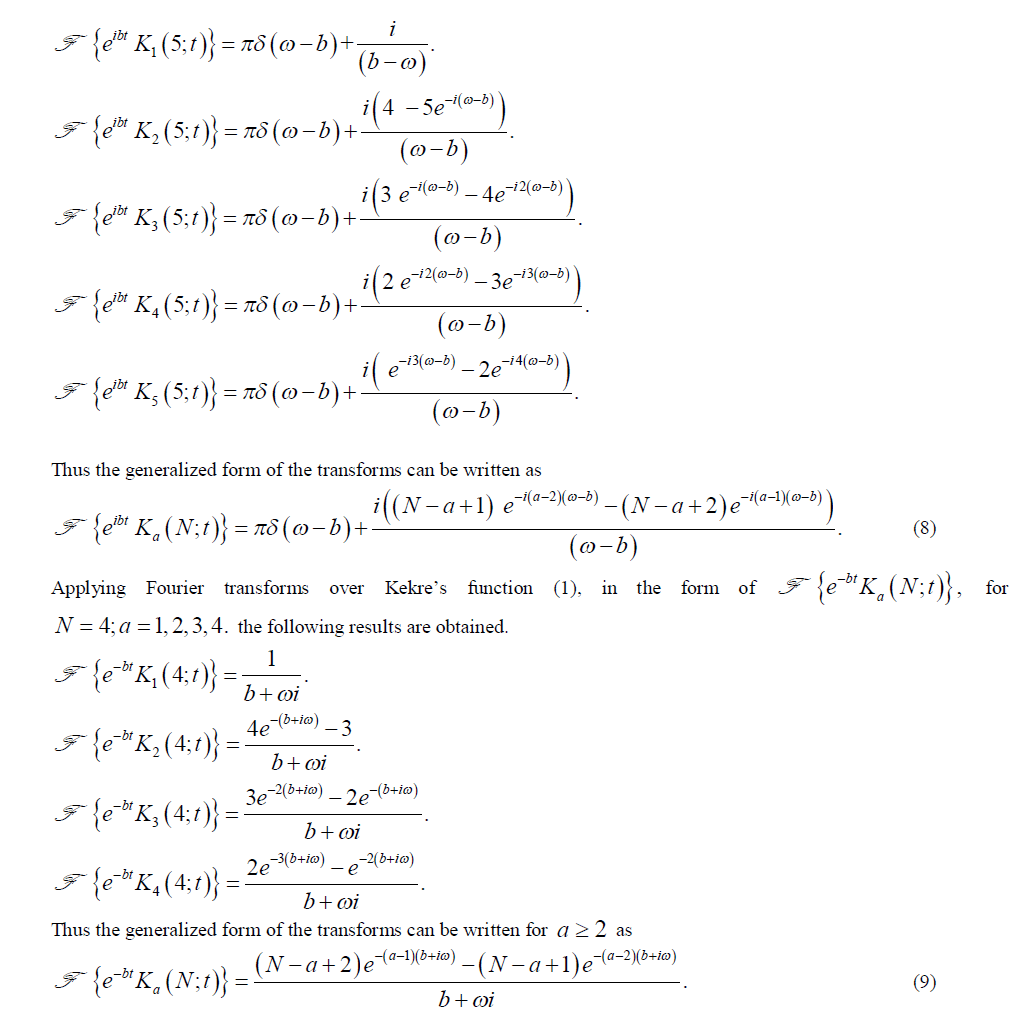RESULT AND DISCUSSION |
| All the examples considering N = 4 or N = 5. These results can be calculated considering for any value of N . The elementary functions using Kekre’s function has been evaluated applying Fourier transforms over it. At the end of examples the generalized representation of the Fourier transforms of Kekre’s function is formulated. These developed Fourier transforms to Kekre’s functions can be applied to applications of pulse radar and Bio-medical applications. |
CONCLUSION |
| Kekre’s function has been used in application to image processing and other computer engineering applications. This paper shows mathematical interpretation of Kekre’s function, such that even Mathematicians can use it efficiently. Results are displayed with their calculations and process of the existence of Kekre’s function applied using Fourier Transforms. |
FUTURE SCOPE |
| This evaluations and observation done by the author in this work can help researchers for the elaborate study using Fourier Transforms to Kekre’s function. Evaluation and analysis can be done for higher orders. Table for all the Fourier transforms to Kekre’s function can be calculated. |
References |
|