ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
K. J. Jegadish Kumar1, S.Sudharsan2 and V.Karthick2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Ubiquitous computing is fetching a significant part in everyone's life. Few such examples are the mobile communication, personal computation and portable hand held devices. The growth in ultra-low power technology enabled the new development of small autonomous mobile devices. For the wireless communication systems with these portable mobile devices, security is a critical factor due to their impact on privacy.. Traditional cryptographic algorithms are much complex and power consuming thereby unfit for this resource constrained applications. In this paper, a novel stream cipher called YUGAM-128 is designed using one dimensional cellular automata (CA) rule 30 and linear feedback shift register (LFSR). The prime aspect of the stream cipher is to generate random 128 bit keystream. The proposed stream cipher is implemented and synthesized in Spartan-3 FPGA device using Xilinx 13.2.
Keywords |
| Cellular Automata; Random number generator; LFSR; Stream Cipher |
INTRODUCTION |
| PSEUDORANDOM number generation by cellular automata (CA) has been an active field of research in the last decade [1], One of the underlying motivations stemming from the advantage offered by the CAs when considered from VLSI viewpoint: CAs are simple, regular, locally interconnected, and modular. These characteristic make them easy easier to implement in hardware than other models, thus making CAs as an attractive choice for on board applications. CA has been traditionally been used to implement RNGs in cryptographic devices [2] and in Built In Self-Test (BIST) circuits [3]. Random number generators play an import rule in several computational fields such as stochastic optimization methods. With the advent of massively parallel scientific computation, the parallel generation of pseudorandom numbers has become essential. With the advent massively parallel scientific computation, parallel generation of pseudorandom number has become essential. |
| The above domains depend critically on the quality of the random numbers as measured by appropriate statistical tests. Moreover, when very long sequences of random numbers are needed, computational efficiency is often of prime import, i.e., The sequence must be produced as rapidly as possible. CAs provide a good solution to this problem, able to produce rapid highquality Random-number streams. |
| One-dimensional CA random number generators have been extensively studied in the past [1], [3], [4], [5]. These studies have shown convincingly the suitability of CA-generated pseudorandom numbers and their superiority with respect to other widely used methods, such as linear feedback shift registers (LFSRs), especially in the case of delay type faults which require pairs of patterns in a specified order [6]. In these works, CA RNGs were essentially handcrafted by studying the structure of the bit patterns generated over time, with theoretical results serving as a baseline offering guidance. |
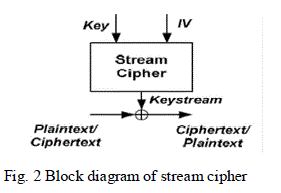
| The mass use of hand-held devices/PDA has popularized the use of stream ciphers. Stream ciphers are much less power consuming, requires small space for their operations and are faster in operation than other cryptographic algorithms. Generally, in stream ciphers a secret key and a public IV are input. Key stream bits are generated by the cipher per cycle of operation. The plain-text is XORed on the encryption side with the generated key stream to produce the cipher-text. Decryption is carried out by simply XORing the ciphertext with the key stream. |
CELLULAR AUTOMATA THEORY |
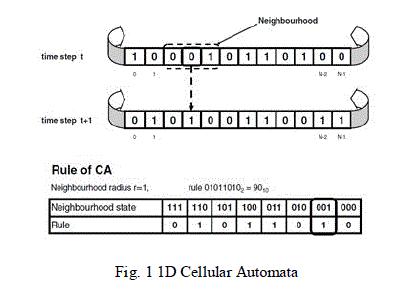
| A cellular automaton (CA) is dynamical systems in which space and time are discrete. A cellular automaton consists of an array of cells, each of which can be in one of a finite number of possible states, updated synchronously in discrete time steps, according to a local, identical interaction rule. Here, we will only consider Boolean automata in which the cellular state, s, 2 f0; 1g. The state of a cell at the next time step is determined by the current states of a surrounding neighbourhood of cells. The cellular array (grid) is ddimensional, where d. 1; 2; 3 is used in practice; in this paper, we shall concentrate on d. 2, i.e., On twodimensional grids. The identical rule contained in each cell is essentially a finite state machine, usually specified in the form of a rule table (also known as the transition function), with an entry for every possible neighbourhood configuration of states. The cellular neighbourhood of a cell consists of itself and of the surrounding (adjacent) cells. For one-dimensional CAs, a cell is connected to r local neighbours (cells) on either side, where r is referred to as the radius (thus, each cell has 2r. 1 neighbours). For two-dimensional CAs, two types of cellular neighbourhoods are usually considered: five cells, consisting of the cell along with its four immediate non diagonal neighbours (also known as the von Neumann neighbourhood) and nine cells, consisting of the cell along with its eight surrounding neighbours (also known as the Moore neighbourhood). In this work, we only consider 5-neighbor grids, thus limiting the already large search-space size; moreover, results exist only for this neighbourhood type, which is also more amenable to hardware implementation. |
| When considering a finite-size grid, cyclic boundary conditions are frequently applied, resulting in a circular grid for the one-dimensional case and in a toroidal one for the two-dimensional case. Fixed, or null, boundary conditions can also be used, in which the grid is surrounded by an outer layer of cells in a fixed state of zero. This case of configuration is usually easier to implement in hardware. |
 |
STREAM CIPHER |
| A stream cipher has a variable message input length, and it can be viewed as a small but changing secret substitution table that transforms plaintext bits at different positions with different substitution tables (the XOR operation between plaintext and key stream can be viewed as one-bit substitution determined by a key stream bit). A stream cipher consists of a state update function and an output function. The state of a stream cipher is updated continuously during encryption so that bits at different positions in a message are encrypted with different states. The output function generates key stream bits from the state and performs encryption or decryption. If the initial state of a stream cipher is not the same as the key, key setup is required to generate the initial state from the key. A key is used with different initialization vectors (IVs) is to generate key streams. The key/IV setup (resynchronization) is required to generate the initial state from the key and IV. |
| The criteria for good stream cipher are, long period with no repetitions statistically random, Large linear complexity (based on the size of equivalent LFSR), Correlation immunity (have the tradeoff with linear complexity), Confusion (output bits depend on all key bits) Diffusion and Use of highly non-linear Boolean functions. |
 |
DESIGN APPROACH |
| A. CA Rule Based Function |
| Rule 30 is a one-dimensional binary cellular automaton rule introduced by Stephen Wolfram in 1983. Wolfram describes it as being his "all-time favourite rule" and details it in his book, A New Kind of Science. Using Wolfram's classification scheme, Rule 30 is a Class III rule, displaying a periodic, chaotic behaviour. |
| This rule is of particular interest because it produces complex, seemingly random patterns from simple, welldefined rules and offers reversible property. Because of this, Wolfram believes that Rule 30, and cellular automata in general, are the key to understanding how simple rules produce complex structures and behaviour in nature. Rule 30 has also been used as a random number generator in Wolfram's program mathematical and has also been proposed as a possible stream cipher for use in cryptography. |
| In all of Wolfram's elementary cellular automata, an infinite one-dimensional array of cellular automaton cells with only two states is considered, with each cell in some initial state. At discrete time intervals, every cell spontaneously changes state based on its current state and the state of its two neighbors. For Rule 30, the rule set which governs the next state of the automaton is given in table I (6) |
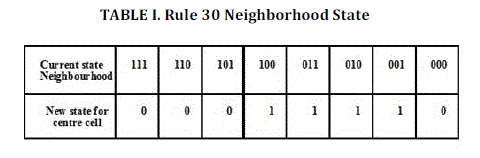 |
| The following pattern emerges from an initial state in a single cell with state 1 (shown as black) is surrounded by cells with state 0 (white). Time increases down the vertical axis. |
| The evaluated function for CA rule 30 is |
 |
| An LFSR consists of clocked storage elements (flipflops) and a feedback path. The number of storage elements gives us the said to be of degree m. The feedback network computes the input for the last flipflop as XOR-sum of certain flip-flops in the shift register Simple LFSR We consider an LFSR of degree m = 3 with flip-flops FF2, FF1, FF0, and a feedback path as shown in Fig. 3. The internal state bits are denoted by si and are shifted by one to the right with each clock tick. The rightmost state bit is also the current output bit. The leftmost state bit is computed in the feedback path, which is the XOR sum of some of the flip-flop values in the previous clock period. Since the XOR is a linear operation, such circuits are called linear feedback shift registers. If we assume an initial state of (s2= 1, s1= 0, s0= 0), Table 2.2 gives the complete sequence of states of the LFSR. Note that the rightmost column is the output of the LFSR. One can see from this example that the LFSR There is a simple formula which determines the functioning of this LFSR. Let’s look at how the output bits si are computed, assuming the initial state bits s0, s1, s2: |
 |
| B. Mathematical Description of LFSRs |
| The general form of an LFSR of degree m is shown in Fig. 2.4. It shows m flip-flops and m possible feedback locations, all combined by the XOR operation. Whether a feedback path is active or not, is defined by the feedback coefficient p0, p1, . . . , pm−1: |
| • If pi = 1 (closed switch), the feedback is active. |
| • If pi = 0 (open switch), the corresponding flipflop output is not used for the feedback. |
| With this notation, we obtain an elegant mathematical description for the feedback path. |
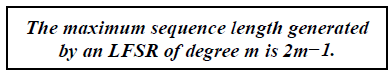 |
| If we multiply the output of flip-flop I by its coefficient pi, the result is either the output value if pi= 1, which corresponds to a closed switch, or the value zero if pi=0, which corresponds to an open switch. The values of the feedback coefficients are crucial for the output sequence produced by the LFSR. |
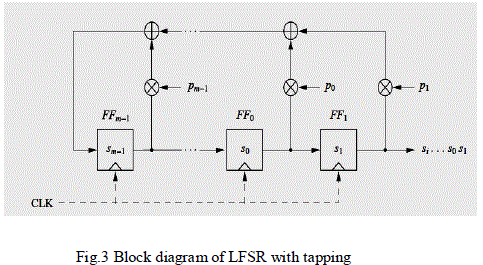 |
| Let’s assume the LFSR is initially loaded with the values s0, . . . , sm−1. The next output bit of the LFSR sm, which is also the input to the leftmost flip-flop, can be computed by the XOR-sum of the products of flip-flop outputs and corresponding feedback coefficient: |
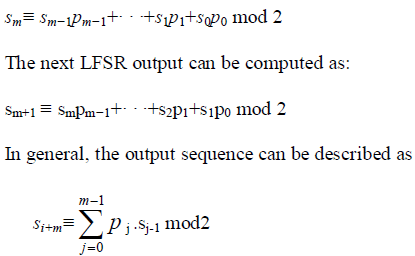 |
| Clearly, the output values are given through a combination of some previous output values. LFSRs are sometimes referred to as umber of recurring states, the output sequence of an LFSR repeats periodically. Moreover, an LFSR can produce output sequences of different lengths, depending on the feedback coefficients. The following theorem gives us the maximum length of an LFSR as a function of its degree. |
| It is easy to show that this theorem holds. The state of an LFSR is uniquely determined by the minterm register bits. Given a certain state, the LFSR deterministically assumes its next state. Because of this, as soon as an LFSR assumes a previous state, it starts to repeat. Since an m-bit state vector can only assume 2m−1 nonzero states, the maximum sequence length before repetition is 2m −1. Note that all zero state must be excluded. If an LFSR assumes this state, it will get “stuck” in it, i.e., It will never be able to leave it again. Note that only certain configurations (p0,. . . , pm−1) yield maximum length LFSRs. We give a small example for this below. |
PROPOSED STREAM CIPHER ARCHITECTURE |
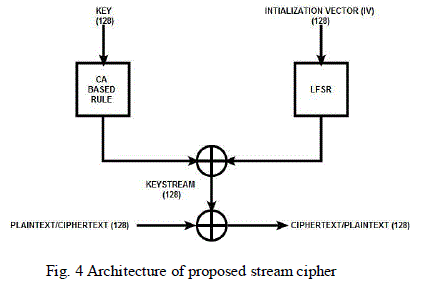
| The figure represents the simple the simplest architecture of the proposed steam cipher using cellular automata. In this architecture, the initial key 128 bit is transformed into unidentifiable form by the cellular automata (CA) rule. The 128 bit in initialization is applied to the linear feedback shift register (LFSR) and then its output is xored with CA rule based update key to generate a key stream per clock cycle. |
 |
HARDWARE IMPLEMENTATION AND SYNTHESIS RESULTS |
| The proposed stream cipher is implemented in SPARTAN-3 xc3vs50-5 pq208 device using Xilinx 13.2. The hardware implementation of the algorithm is very simple as the operator used in the design of stream cipher is flip-flops based hardware circuits. The nonlinearity of the algorithm is decided by the rule 30 CA based pseudo random number generator. The results of the Xilinx Spartan 3 FPGA implementations are shown in Table II. |
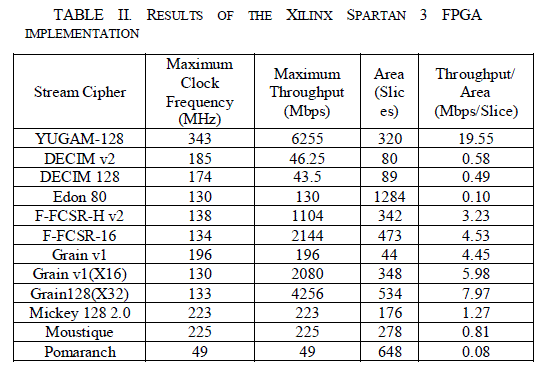 |
| The Xilinx static timing analysis tool is used to determine the maximum clock frequency. Brief overviews of each cipher implementation are given in the following. The ECIM ciphers produced low area implementations due to the simple LFSR structure; however, the through-put was low due to the decimation factor of four. Edon80 was the largest design of the implemented ciphers. The F-FCSR family of ciphers were fairly large (342 slices and 473 slices) compared to the smallest ciphers, but due to the high data radix (8 bits/cycle and 16 bits/cycle), the throughput and through-put/area was relatively high. Grain ranks top in terms of small area and good throughput/area ratio[19]. It was the smallest cipher and the parallelized versions of Grain produced higher throughput/area ratios. Mickey had a medium size area but a good throughput/area ratio; the main disadvantage Mickey had in Xilinx FPGAs were that the S and R registers could not be inferred into Xilinx primitive shift register blocks; thus Mickey in an ASIC implementation may yield better results when compared to the other small ciphers. The same could be said with the F-FCSR family of ciphers. Moustique was of medium-to-large area with a less than one ratio of throughput/area from our design. Moustique was the only self-synchronizing cipher so this should be mentioned in the comparison. Pomaranch was the slowest design and yielded a high area. An implementation using a lookup table of the S-Box was faster (68 MHz) but also larger (1155 slices)[19]. |
CONCLUSION |
| Multimedia information transmission like high quality videos and color still images requires high speed processor for fast processing and transmission over the communication channels. As a result, designing a high speed processing security algorithm has become a challenging issue for the portable computing applications. As a challenge, the proposed YUGAM-128 stream cipher is designed in a simple manner with mere shift registers, whose basic element is flip-flops, XOR and CA functions. This promises efficient implementation in reconfigurable FPGA with high throughput owing to parallelism nature. Hence, the algorithm suits well for the portable computing devices that are facilitated with GHz processors. |
References |
|