International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Fractal Based Space Vector PWM for Three Level Inverter

S.Jeyaseeli
Assistant professor, Dept. of EEE, V V College of Engineering, Tisaiyanvilai, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents a space vector pulse width-modulation technique based on fractal approach for multilevel inverters is presented. Here the properties of fractal structure together with the simplicity of fractal arithmetic are exploited to generate the SVPWM. The proposed method does not use any lookup tables for sector identification. The switching space vectors are also directly determined without using any lookup tables. Simulations are carried out using MATLAB/Simulink for a three level inverter. The proposed scheme can be extended to an n-level inverter, and a generalized algorithm is also presented

Keywords
Fractals, multilevel inverters, space vector Pulse width-modulation (SVPWM).

INTRODUCTION
Multilevel inverters have received a great deal of attention in recent years. In several papers, numerous topologies have been introduced and studied extensively for utilities, traction, and drive application . These inverters are suitable for high-voltage applications because of their ability to synthesize output voltage waveforms with a better harmonic spectrum and attain higher voltages with a limited maximum device rating[2]. Additionally, the harmonic content of output waveform decreases significantly as the number of inverter levels increases .The two main techniques of PWM generation for multilevel inverters are sine-triangle PWM SPWM) and space vector PWM (SVPWM)[3]. SVPWM involves synthesizing the reference voltage space vector by switching among the three nearest voltage space vectors SPWM involves the comparison of a reference signal with a number of level shifted carriers to generate the PWM The two main techniques of PWM generation for multilevel inverters are sine-triangle PWM (SPWM) and space vector PWM (SVPWM) Multilevel SPWM involves the comparison of a reference signal with a number of level shifted carriers to generate the PWM signal. SVPWM involves synthesizing the reference voltage space vector by switching among the three nearest voltage space vectors[4]-[5]. SVPWM is considered a better technique of PWM implementation, owing to its associated advantages as follows: 1) better fundamental output voltage; 2) better harmonic performance; and 3) easier implementation in digital signal processor and microcontrollers.
The implementation of SVPWM involves the following: 1) identification of the sector in which the tip of the reference vector lies; 2) determination of the three nearest voltage space vectors; 3) determination of the duration of each of these switching voltage space vectors; and 4) choosing an optimized switching sequence.
The proposed method uses simple arithmetic for determining the sector and does not require lookup tables. The switching vectors are also directly determined using simple arithmetic and hence do not require lookup tables. All the redundant states of each switching voltage space vector are also generated automatically without using lookup tables.

FRACTAL
Any basic structure that evolves by dividing itself into structures similar to it is said to have fractal structure. A fractal is a fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole by a property called self similarity. It is a powerful tool in computational geometry, and so used in many modern graphics applications. A fractal is a never ending pattern that repeats itself at different scales. This property is called “Self Similarity”. Fractals are extremely complex, sometimes infinitely complex - meaning you can zoom in and find the same shapes forever. Amazingly, fractals are extremely simple to make[1]. A fractal is made by repeating a simple process again and again.certain types of fractals are given below.
i. Natural fractals.
ii. Geometric fractals.
iii. Algebraic fractals.
iv. Mathematical fractals.

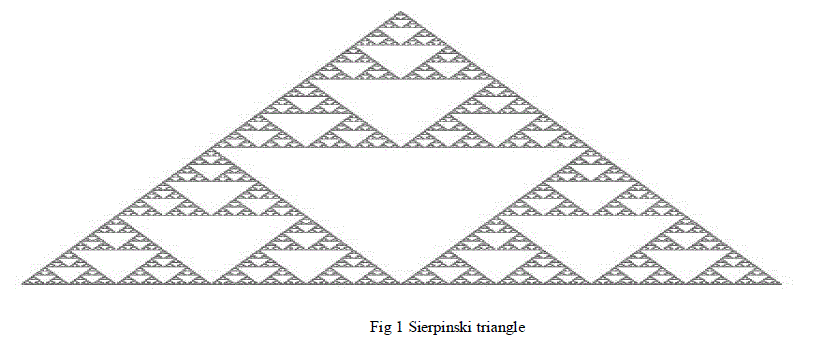
SIERPINSKI TRIANGLE
The basic structure, which is a triangle, is transformed by further dividing itself into smaller triangles. From that point of view, the switching voltage space vector representation of multilevel inverters has a fractal structure where the basic structure is a triangle. In a fractal theory the fractal structure with triangle as basic structure that gets divided into four smaller triangular regions, joined by the midpoints of the sides of the triangle, is called the sierpinski triangle.
IV. PROPOSED METHOD OF GENERATION OF PWM FOR MULTILEVEL INVERTERS THROUGH FRACTALS
The implementation of SVPWM involves the following four stages:
A) Sector identification;
B) Determination of switching voltage space vectors;
C) Determination of the duration of each of the determined switching voltage space vectors; and
D) Determination of an optimum switching sequence.

SECTOR IDENTIFICATION AND SWITCHING VECTOR DETERMINATION
Sector identification determines the triangle that encloses the tip of the reference space vector. In the proposed method,sector identification is done using the principle of repeated triangularization. The vertices of triangle (sector) represent the locations of switching voltage space vectors used to synthesize the reference space vector. From the instantaneous values of the three reference phase voltages Va, Vb, and Vc, the (α, β) coordinates of the voltage space vector are determined. The (α, β) components of the space
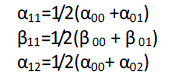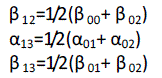image
image
The triangle with centroid closest to tip of reference space vector is ΔA11A12A13.
The sector is identified, and the inverter states corresponding to the switching vectors located at the vertices of the identified sector are also generated simultaneously. vertices of the hexagon forming the periphery are the same as the vectors of equivalent two-level inverter, having the The coordinates of the centroid of an equilateral triangle can be determined as the average of coordinates of the three vertices. represented by a vector of length four (Fig. 2).
image

SWITCHING VECTOR TIME CALCULATION
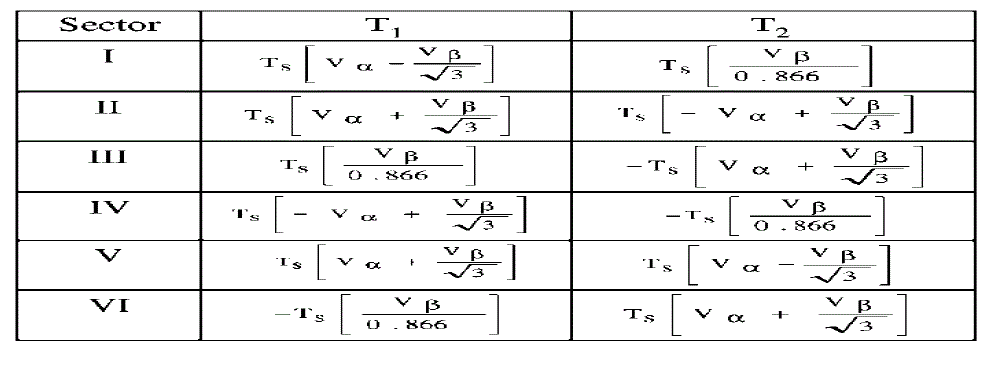
The next stage in the generation of SVPWM through the proposed method involves determining the duration for which the voltage space vectors located at the vertices of the identified sector are to be switched. The determination of the duration of operation of the switching voltage space vectors is simplified by mapping the sector that is identified to enclose the reference space vector to sector of a two-level inverter . The mapping of the identified sector to a sector of the two-level inverter is done by mapping one of the three vectors of the identified sector to the actual zero vector in the voltage space vector representation of the inverter. In this paper, the vector selected to be mapped to the actual zero vector is referred as virtual zero vector. The vector with minimum value for the sum of magnitudes of α and β coordinates is chosen to be the virtual zero vector for a particular sector. The sum of magnitudes of α and β coordinates represents the total offset of the vector from actual zero vector. Therefore, the chosen virtual zero vector is the vector at minimum offset from zero vector. The duration of the third vector (T0), which is the virtual zero vector, is also determined. From the determined T0, T1, and T2, the actual inverter leg switching times, designated as Tga, Tgb, and Tgc, are also determined as in [12]. The Tga, Tgb, and Tgc signals are used to generate the three PWM signals PWM_A, PWM_B, and PWM_C, respectively.
image

OPTIMIZED SWITCHING SEQUENCE SELECTION
Once the switching vectors are determined and their respective durations are calculated, then vectors are to be switched in an optimum sequence such that only one switching occurs when the inverter changes its state. In the space phasor PWM technique, the optimum switching is achieved by using the redundant states of the zero vector for alternate switching cycles. In this paper, the optimum switching is achieved by using two redundant switching states of the respective virtual zero vector in the alternate cycles. For every sector, the switching of the voltage space vectors starts and ends at the redundant states of the virtual zero vector. Therefore, in this paper, optimum switching sequence is achieved by adopting a strategy of selecting the switching state of the virtual zero vectors from the available redundancies. This simple strategy of choosing the switching states from the available redundant states achieves optimum switching in every sector and hence does not require lookup tables.

IN THE OVERMODULATION REGION
In the over modulation region, also the sector identification, switching vector determination, and determination of the virtual zero vector for the sector enclosing the reference space vector are done by utilizing the strategy explained earlier. It may be noted that, during overmodulation, in the case of two-level inverter, zero vector will not be switched and, in the case of multilevel inverters, the virtual zero vector will not be switched so that the entire sampling period is shared by only two vectors. This principle is used to detect the overmodulation region, and after mapping to the twolevel inverter hexagon, T1 and T2 time periods are modified so that Ts = T1 +T2 [6]-[9]. If an overmodulation is detected (i.e., if T0 < 0), the durations of the nonzero switching vectors are modified from T1 and T2 to T|1 and T|2, respectively, as
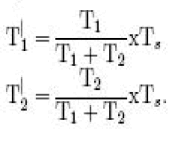image

INVERTER CONFIGURATION
The proposed scheme of generating SVPWM for multilevel inverters can be applied to any generalized inverter configurations like neutral point clamped, H-bridge configuration, capacitor clamped inverters, and open end winding.
The inverter configuration is achieved by feeding the induction motor from both winding ends by two two-level inverters [11]. The inverters I and II switch between the levels zero and Vdc/2, resulting in three voltage levels across the winding of the motor −Vdc/2, zero, and +Vdc/2. The three voltage levels are represented using the digits 0, 1, and 2.

ALGORITHM FOR INVERTER LEG SWITCHING TIME CALCULATION FOR AN n-LEVEL INVERTER
1) Read the instantaneous amplitudes of phase voltages.
2) Determine the coordinates of the instantaneous reference space vector.
3) Normalize the coordinates of the reference space vector through division by VDC/n − 1.
4) Determine the triangular region enclosing the normalized reference space vector for an equivalent two-level inverter.
5) Determine r, which is the number of iterations of steps 6) to 9). Steps 6) to 9) are repeatedly applied on the triangular region in step 4). r is given in (7).
6) Perform a triangularization on the triangular region identified in step 4).
7) Determine the centroid of each of the four triangles given by (7) and (8). Also determine the triangle with centroid closest to the normalized reference space vector.
8) If the number of applications of steps 6) to 9) is r, go to step 11); else, go to step 6).
9) The triangle finally determined in step 9) represents the triangle (sector) enclosing the reference space vector.
10) Select the virtual zero vector from the vectors located at the vertices of the identified sector.
11) Subtract the coordinates of the virtual zero vector from the coordinates of the identified sector.
12) Determine the duration of each switching voltage space vector using conventional equations for a twolevel inverter.
The duration of zero vector T0 =Ts − (T1 +T2). If T0 < 0, go to step 13); else, go to step 14).
13) T0 < 0 implies overmodulation. T1 and T2 are modified according to (9) and (10).
14) Determine the inverter leg switching times using T1 and T2, and generate the PWM.
15) Go to step 1).

SIMULATION RESULTS
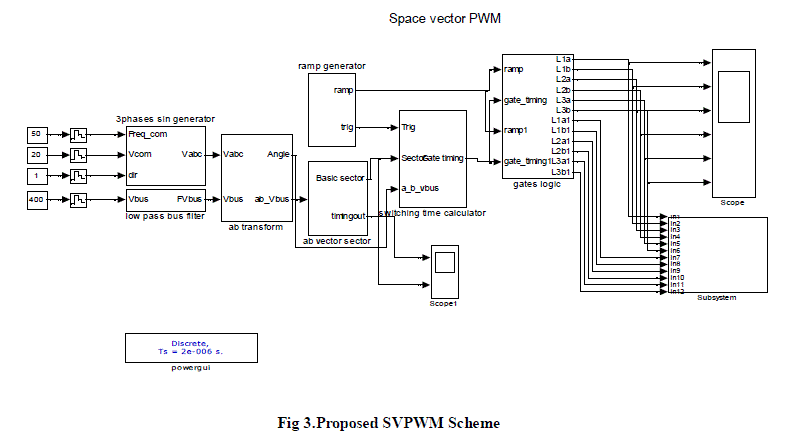
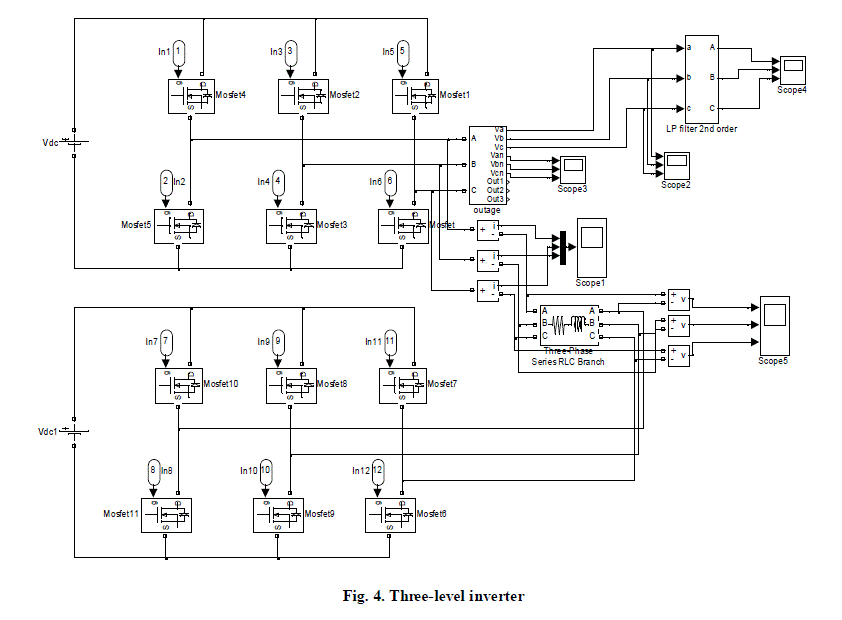
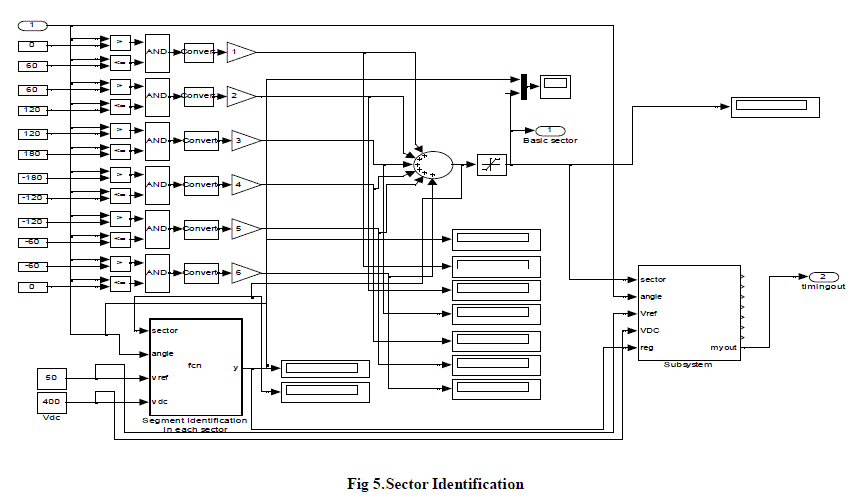
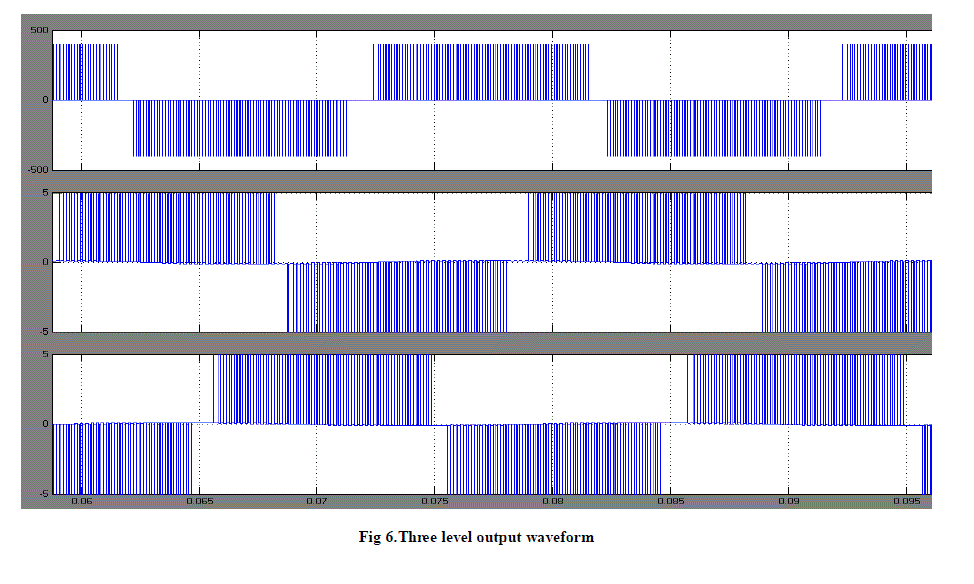
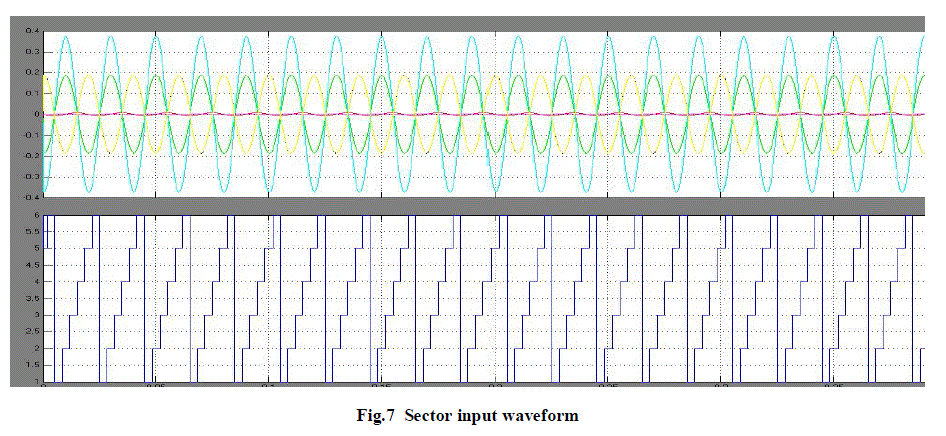
In this paper, the proposed system was simulated using Simulink and Sim Power Systems Toolbox. The simulation circuit of the proposed SVPWM scheme is shown in figure 3. The simulation circuit of the three level inverter and the sector identification are shown in figure 4 and 5. The three level inverter output waveform and the sector input waveform are shown in figure 6 and 7.
image
image
image
image
image

CONCLUSION
In this paper, presented a method of generating SVPWM for multilevel inverters using the fractal structure. The proposed method exploits the features of the fractal representation and the simplicity of fractal arithmetic. The sector identification algorithm proposed does not need lookup tables, and the inverter switching states corresponding to the sector are generated simultaneously along with the sector identification. Optimum switching of the vectors is also achieved without using lookup tables. Simulations are carried out using MATLAB/Simulink.

References