Free Radical Conservation Principle and Conservation Equation Research

Abstract

The purpose of this article is to improve the calculation methods of direct and indirect actions. Through analysis and research on the basic principles of radiation chemistry and radiation biology, as well as the induction and analysis of experimental process and experimental results, it is found that a certain amount of ionizing radiation produces a certain amount of for free radicals; for the same substance, the LET of the rays is different, and the yields of free radicals is different; for the same rays, the yields of free radicals is different for different substances. When the composition of the organism is constant and the water content is the same, a certain amount of radiation will produce a certain amount of free radicals, and a certain amount of free radicals will produce a certain amount of biological effects; when the composition of the organism is constant and achieving the same biological effects, the absorbed dose is inversely proportional to the water content of the organism. The greater the water content of the organism, the smaller the corresponding D37 value, but the total amount of free radicals remains unchanged.

Conclusion: When the environmental conditions of radiation are constant, for the same organism or biological macromolecule, no matter how its water content and D37 value change, the total amount of free radicals when reaching the same biological effect is constant. The free radical conservation equation derived from this principle can not only calculate the magnitude of direct and indirect actions, but also predict the magnitude of radiation effects and the required radiation dose, which plays an important role in the theoretical research and technical application of radiation biology.

Keywords

Radiation effect; Direct action; Indirect action; Free radicals conservation; Calculation method

Introduction

In the radiation process of water-bearing organisms, the effects of rays on organisms include direct and indirect actions. The D10 and D37 values refer to the radiation dose respectively required to kill 90%, 63% of microorganisms and other biological cells or inactivate 90%, 63% of biological active substances by ionizing radiation in the field of radiation biology. They are the characteristic index of traditional radiation biology to measure the radiation sensitivity of different organisms, and mathematical expression of the relationship between the amount of deposition of radiation energy the organism exposed and the damage or even inactivation or death of organisms ^[1].

Direct action means that the energy of the rays directly acts on the constituent substances of the organism, causing these biological macromolecules to be excited or ionized, and then undergoing decomposition and neutralization reactions to generate active biological macromolecular free radicals, which in turn interact with other biological macromolecules. These macromolecules react to generate new macromolecular free radicals. Indirect action means that after the energy of the rays is absorbed by the water molecules, the water molecules are also ionized or excited, and in the subsequent decomposition and neutralization reaction process, e-, •OH, •H and other free radicals are generated ^[2]. Subsequently, the free radicals produced by these two pathways react with other biological macromolecules to generate new macromolecular free radicals, and trigger a series of complex biochemical reactions in the organism, resulting in a variety of biological effects ^[3].

As the gradual increase of water content of organisms or bioactive macromolecules, the indirect actions continue to increase. The radiation sensitivity of organisms or active macromolecules continues to increase and the D₃₇ or D₁₀ value continues to decrease. This phenomenon has attracted widespread attention from researchers in the fields of radiation chemistry and radiation biology. The current research has studied at the molecular level how indirect actions can cause damage to organisms or biological macromolecules and what kind of damage they are subjected. And macroscopically the methods of drying, freezing and adding protective agents are used to measure the direct and indirect actions of radiation. However, these methods are difficult to meet the requirements of scientific research. Therefore, more effective methods for calculating direct and indirect actions must be studied ^[4].

Materials and Methods

Materials

Basic theories and experimental results of radiation biology research.

Methods

By analyzing and summarizing the basic theories and experimental results of radiation biology and radiation chemistry, when reaching the same radiation effect, the principle of free radical conservation and the equation of free radical conservation are derived. And this equation is used to calculate and verify the direct and indirect actions of RNase irradiated by γ-rays with different water content ^[5].

Experimental basis for the principle of free radical conservation

A certain amount of ionizing radiation produces a certain amount of free radicals. For example, 60Co γ-rays are used to irradiate water under normal temperature and pressure. For every 100ev of radiation energy absorbed by water molecules, 5.8 molecules of free radicals will be generated. For the same substance, the LET of the radiation is different, and the yields of free radicals is not the same. For the same LET radiation, the yields of free radicals is also different when the irradiated substances are different ^[6].

A certain amount of free radicals triggers a certain amount of biological effects. The diluting effect of free radicals in radiation biology illustrates that in solution, the number of inactivated solute molecules is related to a fixed number of free radicals. The processes of radiation polymerization, radiation grafting, radiation degradation and radiation crosslinking in polymer radiation chemistry have fully proved this principle. And medical radiation therapy is also a specific application of this principle ^[7].

The dose survival curve of a large number of organisms and biologically active macromolecules fully shows that a certain absorbed dose produces a certain amount of free radicals, and a certain amount of free radicals produces a certain amount of biological effects. The dose required to absorb is the same, which inactivates the same amount of biological macromolecules or kills the equivalent amount of organisms. And the total amount of free radicals produced is the same. The survival rate of organisms on the survival curve drops from 1.0 to 0.37, and then from 0.1 to 0.037. The absorbed dose (i.e., D₃₇ value) of the two processes is the same. This is the most powerful proof ^[8].

According to the definition of radiation biology, no matter what the initial content of organisms or biological macromolecules is, and no matter how big the difference is in the absolute number of actual inactivation, as long as the percentage of damage is the same, it is regarded as the same biological effect. For organisms or biological macromolecules with the same composition and water content, under the same radiation environmental conditions, the required absorbed dose to achieve the same biological effect is the same, and the total amount of free radicals produced is also the same ^[9].

When the water content of biological cells or biological macromolecules changes, the absorbed dose of radiation decreases with the increase of water content when the same biological effect is achieved. However, the total amount of free radicals remains unchanged. This is because a certain amount of biological effect must be caused by a certain amount of free radicals, and a certain amount of free radicals does not require a fixed amount of absorbed dose. Because the yields of free radicals derived from water is higher than that of biological macromolecules, resulting in the absorbed dose triggering a certain amount of free radicals decreases with the increase of water content ^[10].

Radiation inactivation of RNase

RNase with 0 water content is irradiated with γ-rays to inactivate 63%, that is, the absorbed dose is D₃₇. Perform a second irradiation to inactivate 63% of the remaining 37% active RNase, and the cumulative absorbed dose of the two radiations is D'₃₇. RNase with 50% water content is irradiated with γ-rays to inactivate 63%, that is, the absorbed dose is D_{37(50% RNase)}.

Results and Discussion

Results and analysis

When RNase was irradiated for the first time, 63% of RNase was inactivated. When irradiated for the second time, 63% of the remaining 37% active RNase was inactivated. Only 37% × 37% of RNase was active. 63% × 63% of the RNase inactivated by the second radiation is repeatedly irradiated, as shown in Figure 1. The absorbed dose required for the second radiation is still the same as the absorbed dose D₃₇ for the first radiation. These radiation effects are called equivalent biological effects and are all caused by direct actions, and are also the result caused by the same total amount of free radicals (Figures 1 and 2) ^[11].

Figure 1: Schematic diagram of RNase consecutive radiation inactivation effects for twice.

Note:

RNase active molecule,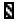

RNase inactivation molecule.

Figure 2: Schematic diagram of 50% RNase radiation effect.

Note: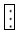

H20 molecules,

RNase active molecule,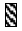

RNase inactivation molecule.

When the water content of RNase increases to 50%, in order to inactivate 50% of RNase by 63%, the amount of free radicals per unit of enzyme molecule must be equal to the amount of free radicals per unit of enzyme molecule during drying. The total amount of free radicals must also be equal. But at this time, the measured D₃₇ (50% RNase) value is lower than half of the D₃₇ value when it is dried. The free radicals generated by direct action cannot meet the requirement of inactivation of 63%, and 50% of the water molecules need to provide the required free radicals. As shown in Figure 2. At this time, part of the inactivation effect is caused by direct action, and the other part is caused by indirect action. The magnitude of direct and indirect action depends on the amount of free radicals provided ^[12].

Through the above experimental results, it can be concluded that when the external conditions of the radiation process (the same LET of the radiation, the same dose rate, the same temperature and pressure during irradiation, the same operation mode of the radiation process, and so on.) are constant, for the same organism or biologically active macromolecules, no matter how their water content and the corresponding D₃₇ value change, the total amount of free radicals when reaching the same biological effect is constant. The radiation inactivation of tobacco mosaic virus and the radiation inactivation experiments of aryl lipase, RNase, sucrose invertase, and alcohol dehydrogenase fully proved this conclusion ^[13].

Derivation of free radical conservation equation

Related concepts and basic parameters: Absorption coefficient, refers to the share of energy absorbed by certain substance when γ-ray or χ-ray passes through the substance with unit thickness. Unit: m²/kg.

The mass-energy absorption coefficient of biomaterials for γ-rays with an average energy of 1.25 MeV is calculated as follows.

μ_en/ρ=2.6691+2.6419y              (1)

In formula 1,

μ_en/ρ, mass energy absorption coefficient of a biomaterial, unit: 10^-3m²/kg.

y, hydrogen content of a biological material.

Calculation of mass energy absorption coefficient of H₂O: Calculated from the molecular formula of H₂O, yH₂0=0.111898. yH₂0 Substituted into formula 1, (μ_en/ρ)H₂O=2.965 × 10^-3m²/kg.

The yields of free radicals refers to the amount of free radicals produced by a specific substance absorbing 100eV of radiant energy, since it is impossible to specifically measure the radiant energy absorbed by various substances in a radiation experiment, the absorbed dose of the irradiated substance could be measured, and then by the mass energy absorption coefficient to be converted into the radiant energy absorbed by a specific substance ^[14].

Mass energy absorption coefficient of potassium dichromate silver (KAgCr₂O₇) dose agent.

According to literature, (μ_en/ρ)KAgCr₂O₇=2.960 × 10^-3m²/kg. Conversion of absorbed dose

D_m=(μ_en/ρ)_m/(μ_en/ρ)_d × D_d             (2)

In formula 2,

D_m- absorbed dose of a substance to be being measured, unit: Gy.

(μ_en/ρ)_m- mass energy absorption coefficient of a substance tested, unit: m²/kg.

D_d- absorbed dose of a substance to be been tested, unit: Gy.

(μ_en/ρ)_d- mass energy absorption coefficient of a substance to be been tested, unit: m²/kg.

Dose absorption rate of H₂0

The following two algebraic modules substituted into formula 2, (μ_en/ρ)KAgCr₂O₇=2.960 × 10^-3m²/kg, (μen/ρ)H2O=2.965 × 10^-3m²/kg, then calculated, DH₂O=1.0017DKAgCr₂O₇.

Free radical yield of H₂0

The amount of free radicals produced from water irradiated by a certain dose of ray, unit: mol/J.

According to the literature, GH₂0=5.8 molecules/100ev, which is converted to, GH₂0= 6.0088 × 10^-7mol/J.

Free radicals conservation equation

Calculation formula of free radicals yield (M_m) of biological macromolecule in organisms

According to the definition of free radicals, M_m=W × D_m × G_m            (3)

In formula 3,

W- Mass fraction of biological macromolecules in the organism, unit: kg, 0<W ≦ 1.0.

D_m- Absorbed dose of biological macromolecules in organism, unit: Gy.

G_m- Free radical yields of biological macromolecules in organisms, unit: mol/J.

Calculation of free radical yield (MH₂O) of water in organisms

MH₂O=(1-W) × DH₂O × GH₂O            (4)

In formula 4,

1-W-Mass fraction of water in organism, unit: kg, 0<1-W ≦ 1.0.

DH₂O-Absorbed dose of water in organism, unit: Gy.

GH₂O-Free radical yields of water in organism, unit: mol/J.

Calculation of total free radicals (M_t)

M_t=DKAgCr₂O₇ × (W × D_m × G_m+1-W）× DH₂O × GH₂O)             (5)

In formula 5,

DKAgCr₂O₇- Absorbed dose corresponding to a certain biological effect, unit: Gy.

Free radicals conservation equation

According to the definition of the total amount of free radicals and the principle of free radicals conservation ^[15].

D_i × (W_i × D_m × G_m+(1-W_i) × DH₂O × GH₂O)

=D_n × (W_n × D_m × G_m+(1-W_n) × DH₂O × GH₂O)                 (6)

In formula 6,

D_i, D_n-Absorbed dose of organisms or bioactive macromolecules with different water content when the same biological effect caused, unit: Gy.

Application conditions and functions of free radical conservation equation

Prerequisites for applying free radical conservation equation: To apply the free radical conservation equation to study the influence of radiation external conditions, radiation dose, and total amount of free radicals on radiation effects, the following preconditions must be met ^[16].

• The organism to be studied must be the same species or the same substance, and the internal components should be the same except for with the different water content.
• The external conditions (LET, dose rate, temperature, pressure, etc.) of the radiation must remain unchanged.
• If the influence of other parameters except the composition and water content on the radiation effect need to be measured (such as: dose rate effect, temperature effect, oxygen effect, protective agent, etc.), only one item can be set once, and other items should be constant ^[17].

Function of free radical conservation equation

• Through indirect measurement of the water content of the organism and the corresponding D₃₇ value, the measurement and calculation method of the free radical yields of biological cells with more than hundreds of components, which is difficult to measure, becomes simple and feasible [18].
• It can directly calculate the direct and indirect actions of the water containing biological system through the difference in the yields of free radicals between biological macromolecules and water molecules, avoiding that the drying method is not suitable for higher biological cells, and the freezing method underestimates the direct action. The method of adding protective agents also overestimates the impact of direct action ^[19].
• According to the water content of the organism, the radiation dose can be set to predict the radiation biological effect that will occur, and the radiation technical parameters that should be used can also be calculated according to the required biological effect ^[20].

Application of free radical conservation equation

Calculation of absorbed dose of RNase: The H content of RNase calculated from the molecular formula of RNase (C₉H₁₄N₄O₃) is 0.06237. The D₃₇ value of RNase was obtained from literature, which are D_{37 (RNase)}=420 kGy, D_{37 (0.5%RNase)}=4.0 kGy.

The H value and D₃₇ value are substituted into formula 1 and formula 2 and calculated, then obtained D_RNase=0.9574 DKAgCr₂O₇.

Calculation of free radical yields of RNase

D_H20=1.0017 DKAgCr₂O₇, DRNase=0.9574 DKAgCr₂O₇, GH₂0=600.088 × 10^-9 mol/J, D_37(RNase)=420 kGy, D_{37(0.5%RNase)}=4 kGy.

The algebraic value above are substituted into formula 6 to calculate, and obtained G_RNase=5.958 × 10^-9 mol/J.

Calculation of free radical of RNase and value of D37 at low water content

Let the water content of RNase be: 0.00, 10%, 20%, 30%, 40%, 50% and 60%. The values of including water content and related parameters of DH₂0, D_RNase, G_H20 and G_RNase were substituted into formula 3, formula 4, and formula 6. The percentage of direct and indirect action (That is: free radicals percentage) and the corresponding D₃₇ value at different water content was calculated. The results are shown in Table 1.

Table 1. Ratios of indirect and direct action and corresponding D₃₇ values at different water contents.

In Table 1, the quantitative calculation results by the free radical conservation equation show that when RNase is in a dry state, the biological effects of radiation are completely produced by the direct action of rays. The D37 value is as high as 420 kGy without indirect action at this time. When the water content rises to 10%, more than 90% of the radiation effect is produced by the indirect action derived from water radiolysis, and the direct action ratio is less than 10%, and the D37 value drops from 420 kGy to 36.73 kGy. When the water content of RNase reaches 50%, the ratio of direct action is less than 1%. These calculation results are consistent with radiation biology theory and research results ^[21].

Calculation of free radical of RNase and D₃₇ value at high water content

Let the water content of RNase be: 0.99500, 0.99750, 0.99900, 0.99950, 0.99975, 0.99990. The values of water content and related parameters are substituted into formula 3, formula 4, and formula 6 and calculated. The results are shown in Table 2.

Table 2. Ratios of free radical and values of D₃₇ in dilute solution of RNase.

In Table 2, the quantitative calculation results of the free radical conservation equation show that when the water content of RNase reaches 99.50%, the biological effects of radiation are mainly caused by indirect action, and the ratio of direct action is less than 5/100,000. When it reaches 99.90%, the direct action ratio is less than one hundred thousandths. Its D₃₇ value also drops below 4.00 kGy, and gradually changes linearly. These quantitative calculation results are consistent with actual results. See Figure 3 for details ^[22].

Figure 3: Curve of D₃₇ in dilute solution of RNase.

This result is completely consistent with the research result of Yijing Chen. It also shows that the free radical conservation equation is in line with objective reality ^[23-26].

Conclusion

The application of free radical conservation equation can not only calculate direct and indirect actions of different water content, but also reveal the change trajectory of radiation energy track control process and free radical diffusion control process in the radiation process. The physical and chemical processes of radiation are closely integrated, which is conducive to the research of radiation biology.

The free radical conservation equation can predict the degree of biological effect according to the different water content of the organism and radiation dose. It can also calculate the radiation technical parameters that should be used according to the expected biological effect, which plays an important role in the application of radiation biotechnology.

Theoretically, the influence of various environmental factors on radiation effect can be calculated by the free radical conservation equation, as well as the influence of sensitizers, protective agents and other impurities in the internal environment on the radiation effect.

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

Special thanks to Professor Christopher Chantler of Melbourne University, Professor Maolin Zhai of Peking university and professor Yimin Ha of Chinese academy of agricultural sciences for their valuable suggestions and support during the study. Thanks to national key research and development project (No. 2019YFD0902000) and Guangzhou people’s livelihood science and technology project.

Author Contributions

H.Z.X. constructed the concept and methodology, and wrote the original manuscript. S.H.W. inquired and collected datas. J.H.Q. tested and verified results. L.T. provided fund support and managed project progress.
Y.X.C. reviewed the manuscript. M.L.C. wrote, reviewed and edited manuscript.

Competing Interests

The authors declare no competing interests.

References

1. Rodemann HP, et al. Responses of normal cells to ionizing radiation. Semin Radiat Oncol. 2007;17:81-88.

   [Crossref] [Google Scholar] [PubMed]

2. Hall EJ, et al. Radiobiology for the radiologist. 8th edition. Lippincott Williams and Wilkins publications. Pennsylvania, US. 2019;67-110.

   [Google Scholar]

3. Gong SL, et al. Radiation cytobiology. 1st edition. China atomic energy press. Beijing, China. 2014;12-40.
4. Ruchardt C, et al. Basic principles of reactivity in free radical chemistry. Free Radic Res Commun. 1987;2:197-216.

   [Crossref] [Google Scholar] [PubMed]

5. Liu SZ, et al. Medical radiobiology. 3rd edition. China atomic energy press. Beijing, China. 2010:6-31.
6. Hoe ST, et al. Free radical reactions with proteins and enzymes: The inactivation of bovine carbonic anhydrase B. Biochim Biophys Acta. 1981;662:55-64.

   [Crossref] [Google Scholar] [PubMed]

7. Rao VS, et al. The relative efficiency of radicals in radiation damage to deoxyribose. Free Radic Res Commun. 1991;12:67-73.

   [Crossref] [Google Scholar] [PubMed]

8. Qiu GY, et al. Radiation biophysics. Wuhan university press. Wuhan, China. 1990;54-113.
9. Hitschke K, et al. Inactivation of the Na, K-ATPase by radiation induced free radicals evidence for a radical chain mechanism. FEBS Lett. 1994;353:297-300.

   [Crossref] [Google Scholar] [PubMed]

10. Yamazaki I, et al. Free radical mechanisms in enzyme reactions. Free Radic Biol Med. 1987;3:397-404.

    [Crossref] [Google Scholar] [PubMed]

11. Geng YS, et al. A study on the resistance and stability of bacillus pumilus E601 against radiation. Chin J Epidemiol. 1999;20:334-337.

    [Google Scholar]

12. Kong QL, et al. The effect of E-beam irradiation on the sterilization for calcium lactate. J Radiat Res. 2011;29:33-37.

    [Google Scholar]

13. Ballarini F, et al. From DNA radiation damage to cell death: Theoretical approaches. J Nucleic Acids. 2010:1-8.

    [Crossref] [Google Scholar] [PubMed]

14. Shao CL, et al. Mechanisms of formation of DNA strand breaks induced by γ-Rays. Sheng Wu Hua Xue Yu Sheng Wu Wu Li Xue Bao. 1999;31:159-162.

    [Google Scholar] [PubMed]

15. Osman R, et al. Molecular mechanisms of radiation induced DNA damage: H-addition to bases, direct ionization and double strand break. Free Radic Res Commun. 1991;13:465-467.

    [Crossref] [Google Scholar] [PubMed]

16. Kelsey CA, et al. Radiation biology of medical imaging. 1st edition. John Wiley and Sons Inc. New Jersey, Canada. 2014;125-140.

    [Google Scholar]

17. Luo XL, et al. DNA strand breaks and crosslinks induced by transient anions in the range 2-20 eV. J Chem Phys. 2014;140:155101-155111.

    [Crossref] [Google Scholar] [PubMed]

18. Milligan JR, et al. Variation of single strand break yield with scavenger concentration for plasmid DNA irradiated in aqueous solution. Radiat Res. 1993;133:151-157.

    [Google Scholar] [PubMed]

19. Jones GDD, et al. Yield of strand breaks as a function of scavenger concentration and LET for SV40 irradiated with 4He ions. Radiat Res. 1993;136:190-196.

    [Google Scholar] [PubMed]

20. Siddiqi MA, et al. Single and double strand break formation in DNA irradiated in aqueous solution: Dependence on dose and OH radical scavenger concentration. Radiat Res. 1987;112:449-463.

    [Google Scholar] [PubMed]

21. Vysin L, et al. Proton induced direct and indirect damage of plasmid DNA. Radiat Environ Biophys. 2015;54:343–352.

    [Crossref] [Google Scholar] [PubMed]

22. Huang GL, et al. Fundamentals of radiation chemistry of polymers. Sichuan university press. Chengdu, China. 1993:328-356.
23. Alpen E, et al. Survival curve and its significance. Radiation biophysics, academic press. Newyork, USA. 1998;169-193.
24. Seymour CB, et al. Relative contribution of bystander and targeted cell killing to the low dose region of the radiation dose response curve. Radiat Res. 2000;153:508-511.

    [Crossref] [Google Scholar] [PubMed]

25. Zheng Z, et al. Mass energy absorption coefficient of biomaterials and its calculation formula. Nucl Agr Bull. 1997;18:63-71.
26. Chen YJ, et al. Study on radiation induced deactivation of catalase in dilute aqueous solution and protective effect. J Radiat Res. 1993;11:18-22.