ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| Dr.T.V.U.Kiran Kumar HOD, Dept Of ECE, Bharath University, Chennai-600073, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Biomedical signal compression has been increasing interest due to the need of storing or transmitting large amount of multichannel data. Wavelets and wavelet packets have recently emerged as powerful tools for signal compression. A novel scheme for signal compression based on the discrete wavelet packet transform (DWPT) decomposition was proposed. The mother wavelet and the basis of wavelet packets were optimized and the wavelet coefficients were encoded with a modified version of the embedded Zero tree algorithm. The internal optimization was the best basis selection that was performed for a given mother wavelet. In conclusion, best basis selection and optimization of the mother wavelet through parameterization led to substantial improvement of performance in signal compression with respect to DWT and random selection of the mother wavelet.
Keywords |
| Compression Ratio(CR),Discrete Wavelet Packet Transform(DWPT),Embedded Zero tree Wavelet (EZW),Percent Residual Difference(PRD). |
INTRODUCTION |
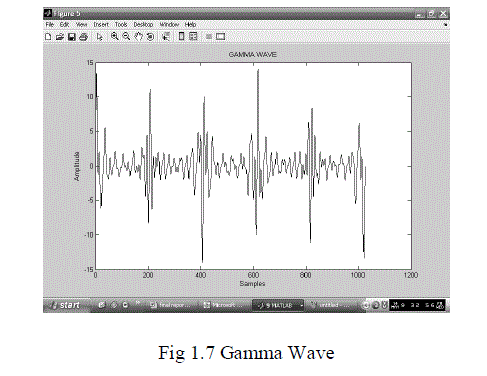
| The human body is able to successfully function as a single system through the integrated communication of electrical pulses known as action potentials. The electrical activity at the cellular level can be traced by the origin of action potentials .Neurons are cells highly specialized for their electrical function and use their membranes to maintain electrochemical gradients of sodium, potassium, calcium, and chloride ions. Generally speaking, there is a higher concentration of potassium on the cell’s interior and a higher concentration of sodium in the extra cellular matrix.The electroencephalography (EEG) measures brainwaves of different frequencies within the brain. The raw EEG has usually been described in terms of frequency bands;(i)DELTA(less than 4 Hz);(ii)THETA (4-8 Hz);(iii)ALPHA (8-12 Hz);(iv)BETA (13-30Hz);(v)GAMMA greater than 30(Hz). |
| Data compression algorithms are used to reduce the number of bits required to represent an image or a video sequence. Data compression treats information in digital form that is, as ones and zero numbers represented by bytes of data with very large data sets. The solution is to increase the bandwidth but high cost makes this less attractive. Therefore, compression is necessary and an essential method for creating image files with manageable and transmittable sizes. |
| Compression takes an input X and generates a representation Y that hopefully requires fewer bits. To generate the reconstruction Z, a reconstruction algorithm operates on the compressed representation Y. Data compression can be divided into two types based on the reconstruction. One is lossless compression, in which Z is identical to X. Run Length coding, Huffman coding, Lempel-Ziv algorithms, and Arithmetic coding are examples of lossless methods. Much higher compression is achieved in lossy compression compared to lossless but Z to be different from X. |
METHODS |
| (i)Transform: Representation of signal in another form is called transform. It does not change the information content present in the signal. Mathematical transformations are applied to signals to obtain further information from that signal that is not readily available in the raw signal. There are a number of transformations that can be applied. |
| (ii)Wavelets: Mathematical functions that cut up data into different frequency components are called wavelets. The main advantages are to analyze discontinuities in higher derivatives, sharp spikes, trends, breakdown points, and self-similarity. .Wavelet analysis is capable of revealing aspects of data that other signal analysis techniques miss and can often de-noise or compress a signal without appreciable degradation. One major advantage afforded by wavelets is the ability to perform local analysis - that is, to analyze a localized area of a larger signal. A wavelet is a waveform of effectively limited duration that has an average value of zero. |
 |
| (iii)Wavelet Transform: A time-frequency representation of the signal is obtained by using wavelet transform.. To overcome the shortcoming of the Short Time Fourier Transform (STFT), which can also be used to analyze non-stationary signals wavelet transform was developed. The main disadvantage of STFT is a constant resolution at all frequencies. Multi-resolution is a technique used to analyze different frequencies with different resolutions it is used in wavelet transform. An oscillating function of time or space is called a wave and is periodic. In contrast, wavelets are nothing but localized waves. |
| Discrete Wavelet Packet Transform(DWPT): The wavelet packet method is a derivation of wavelet decomposition that offers a richer analysis of signal. Wavelet packet has three parameters: position, scale and frequency. We generate a library of bases called wavelet packet bases-for a given orthogonal wavelet function. Preserving global energy, and reconstructing exact feature-each of these bases offers a particular way of coding signals. For numerous expansions of a given signal the wavelet packets can be used. The most suitable decomposition of a given signal is selected with respect to an entropy-based criterion. |
| Best Basis Selection in DWPT:The DWPT decomposition can be seen as a binary tree in which each node represents either a space Wj p or the related coefficients Cj p ={wjp[k]}0≤k<N /2 j). This signal representation is highly redundant since each node space is the direct sum of its two children. To obtain a non redundant and still invertible representation of the signal, the full tree can be pruned by selecting a set of subspaces within the tree. This selection is performed by choosing two children between their parent. The leaves of the resulting tree constitute a decomposition of the initial space V0 . For a tree of depth J, the number of possible decompositions of V0 is NJ = N 2J−1+1 with N0 =1. |
| This large collection of wavelet packet bases must be explored to find a pertinent basis for a given signal and a given mother wavelet. An exhaustive search is not easible, given the large number of possible decompositions. Wickerhauser and Coifman [9] proposed a fast algorithm along with an additive information cost function to prune the full wavelet packet tree. A map M from sequences {xi} to R is called an additive information cost function if M(0) = 0 and M{x j} = M(x j ) Σj . Given such a map, a full wavelet packet tree can be fast pruned [order O(N log N) ] to find the basis B that minimizes M(Bx) with a bottom-up series of decisions to keep children nodes (split) or to keep parent node (merge). |
EMBEDDEDZEROTREE WAVELET ALGORITHM |
| A wide variety of encoding methods have been developed for wavelets, and of these, the EZW encoding introduced by Shapiro [5] is one of the most powerful. The EZW algorithm obtains the best reconstructed signal quality for a given bit rate under the constraint that the encoding is embedded. With an embedded encoding, all encodings of the signal at a lower bit rate are embedded as prefixes of the bit stream for the target bit rate, and therefore, the transmission and decoding of compressed data can be stopped at any point and a signal can be reconstructed. The following presentation of the EZW algorithm was inspired by that in. |
| The EZW algorithm is based upon: 1) prioritized transmission of the location and sign of a signal’s “significant” wavelet coefficients; 2) compactly encoding the locations of non significant coefficients by exploiting the self-similarity of the wavelet transform across scales; and 3) successive approximation of significant coefficient magnitudes via ordered bit plane transmission of coefficient data. A coefficient’s significance is determined by comparing its magnitude with a set of octavely decreasing thresholds; a coefficient is significant with respect to a particular threshold if its magnitude is greater than or equal to that threshold. |
| The forward wavelet transform decorrelates a signal and concentrates its information into a relatively small number of coefficients with large magnitude. These large coefficients contain more energy than the small coefficients, and thus are more important to the reconstructed signal quality than the small coefficients. Therefore, the EZW prioritization scheme transmits the large (significant) coefficients before transmitting the smaller coefficients. The threshold is lowered by a factor of two for each pass this is accomplished by making multiple passes over the wavelet coefficients. |
| On each pass, the coder refines the magnitude value of each coefficient determined to be significant during previous passes and then searches through the coefficients previously considered to be insignificant, encoding information regarding the significance of each with respect to the new threshold. To reduce the amount of information transmitted, the EZW coder takes advantage of the observation that if a wavelet coefficient cv,k at a coarse scale is insignificant with respect to a given threshold, it is highly likely that all the wavelet coefficients in the same spatial location at finer scales, i.e., the descendants of cv,k in the hierarchical pyramid, will also be insignificant with respect to the threshold. If this is indeed true, we say that cv,k is the root of a zerotree. By encoding that is a zerotree root, we compactly specify that its (possibly numerous) descendants are insignificant. |
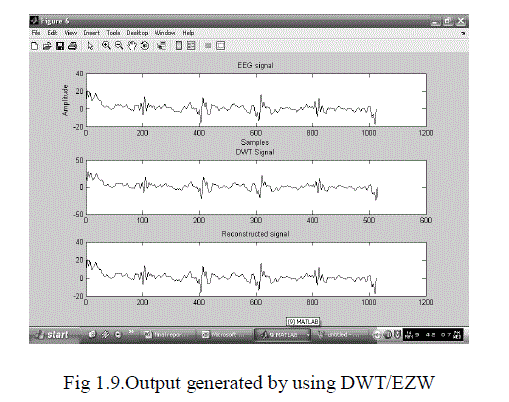
| Compression scheme: The overall compression algorithm is separated in two stages. The DWPT of the signal is first computed for a given vector value θ (mother wavelet parameterization). Then, using a cost function, the wavelet packet tree is pruned according to the best basis algorithm presented above. This stage is lossless and its output is another representation of the signal. However, for transmission purposes, the size of the output of the DWPT is larger than the original number of samples since the tree structure corresponding to the best basis must also be transmitted together with the transformation coefficients. If we assume that each basis is equiprobable, then for NJ possible bases, log2(NJ ) bits will be needed to code the basis.The decoding and inverse transformation blocks perform the inverse of these two stages to reconstruct the signal. The distortion metric used to quantify the difference between the original signal x[k] and the reconstructed signal xˆ[k] after decoding is the percent residual difference (PRD): |
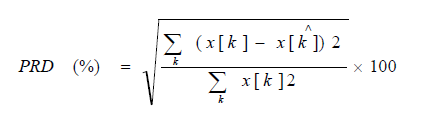 |
 |
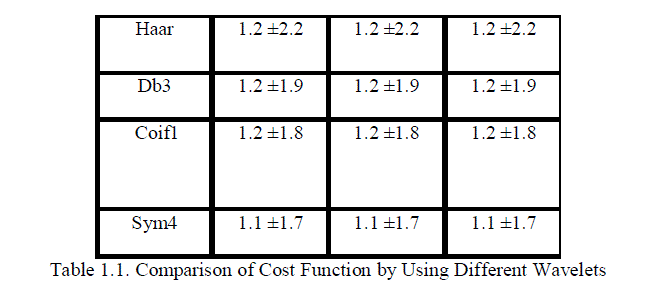 |
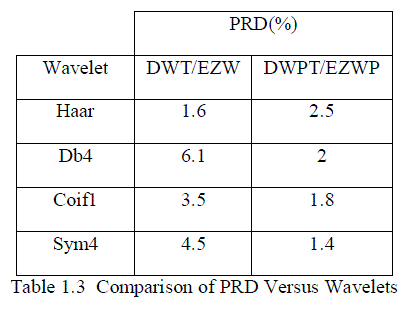
| We observe that Symlet4 orthogonal wavelet achieve lowest PRD among the tested wavelets from the above table. |
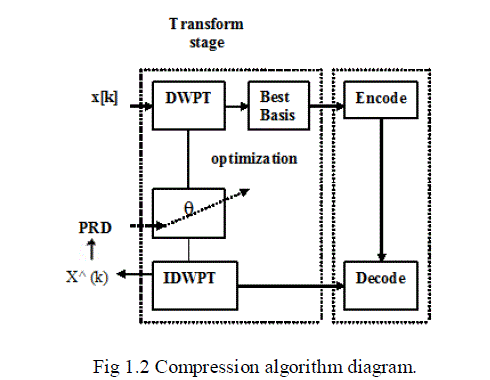
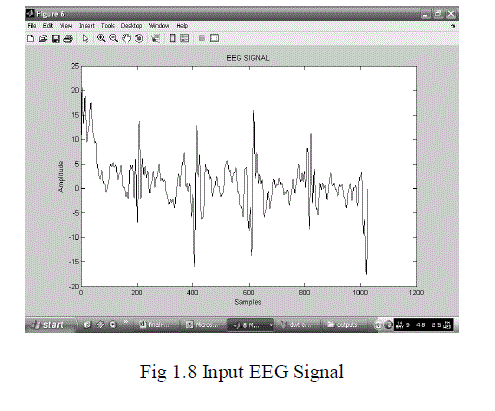
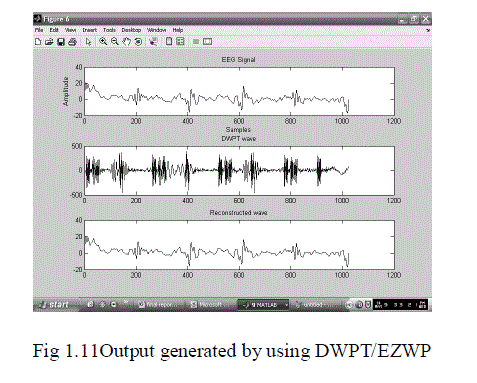
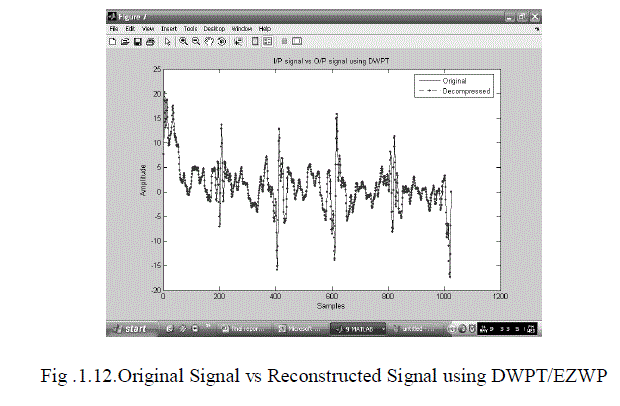
| In the figure 6.3 x (k) is the input to the compression algorithm. The discrete wavelet packet transform(DWPT) decorrelates the individual samples. The transformed representation of x(k) is passed as input to the embedded zerotree wavelet (EZWP) coding scheme. The encoding process continues until a predefined target bit rate is met. When this happens, the decoding process initiates. The IDWPT block carries out the inverse DWPT on the decoded wavelet coefficients, and it returns a distortion metric PRD and the reconstructed signal x^(k). The distortion metric is compared among the set of parametrized wavelets and its minimum identifies the optimal wavelet. h is the parameter vector which defines the wavelet. Once the optimal wavelet is selected, it is used to compress the signal to be transmitted or stored DWPT and EZWP are repeated for all values of a predefined set of values of the parameter vector θ and the θ value leading to the minimum PRD is chosen as representing the best mother wavelet (wavelet optimization). The internal optimization is the best basis selection that is performed for each mother wavelet. |
RESULTS AND DISCUSSION |
| A compression algorithm based on wavelet packets and mother wavelet optimization has been proposed. The algorithm is an extension of the DWT optimization proposed in [3] with the inclusion of the best wavelet packet tree to represent the signal. This constitutes a more flexible mapping of the frequency plane than the DWT and is the first approach that combines optimization of the scaling filter and of the wavelet packet for compression. Depending on the signal type, the parameterization of the mother wavelet and the best basis selection were shown to have an impact in reducing the PRD. |
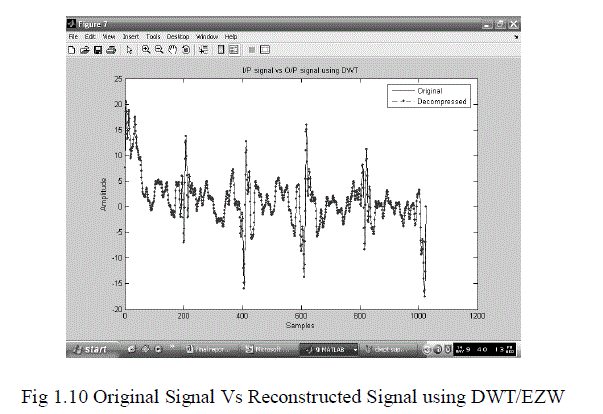
| The results showed that wavelet optimization with DWT improve the quality of the decoded signal with respect to classic wavelets. Optimization of the mother wavelet also resulted in reduced PRD in case of DWPT. Since the distortion rate cannot be predicted, a mother wavelet could not be selected a-priori but should be based on the signal characteristics. |
 |
| The separation between subbands is performed by filters whose selectivities depend on the mother wavelet and whose bandwidths depend on the packet selected. Joint optimization of the mother wavelet and of the wavelet packet corresponds to the optimal subband analysis in terms of filter transfer function and bandwidths for the purpose of compression. |
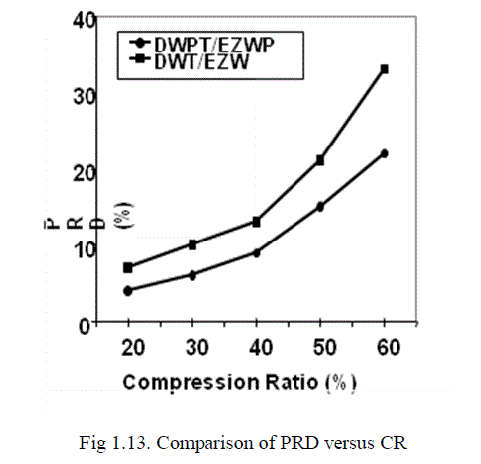
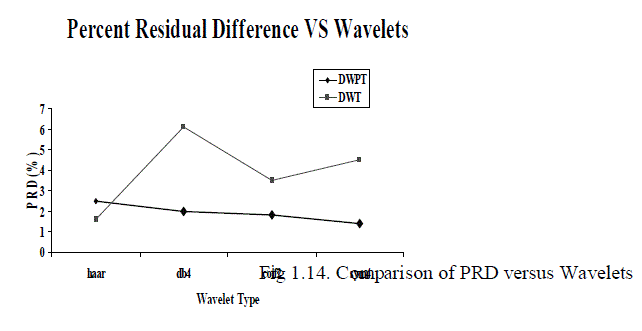
| The best basis selection resulted in a further decrease in PRD with respect to DWT for EEG signals. In this case, DWPT with Coiflet and Symlet wavelets performed better than DWT with optimal wavelet indicating that the best basis for EEG compression is very different from the dyadic wavelet basis.A basis optimization is thus necessary. Table 1.1 shows that the cost function did not significantly influence the results, thus any of the three cost functions compared can be used. However, it is underlined that the proposed optimized DWPT/EZWP method does not result in significant worsening of performance even when the optimal basis is close to the dyadic one. Its application may provide large or more limited improvement over classic DWT depending on the signal type. In particular, the DWPT/EZWP approach with best basis selection performs consistently worse than the DWT/EZW in case of worst wavelet. |
| Methods comparison: The method proposed (DWPT/EZWP) has been compared with DWT/EZW with classic wavelets which has been used in [4].The improvement in performance due to the optimization of the mother wavelet and to best basis selection comparing a number of possible wavelet approaches. The present work focused only on wavelet compression schemes. In addition, the encoder chosen (EZWP) is naturally adapted to the hierarchical DWPT transformation but any other encoding scheme could be used with the proposed optimization. The current study aimed mainly at proposing a sub band signal decomposition optimized for the purpose of compression while the specific encoding scheme was of smaller interest. |
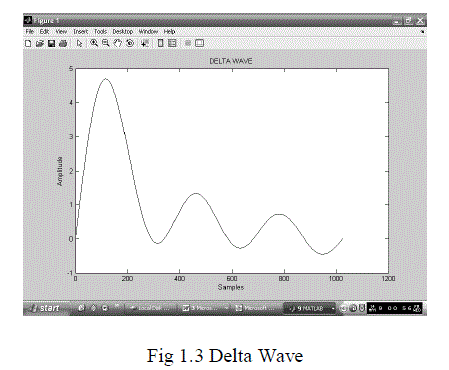 |
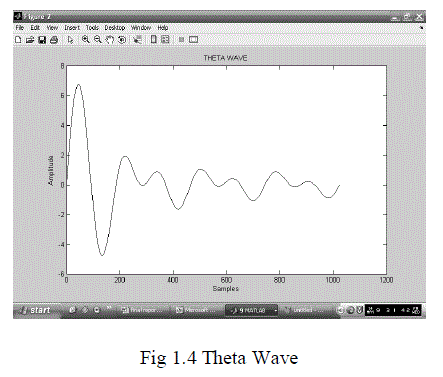 |
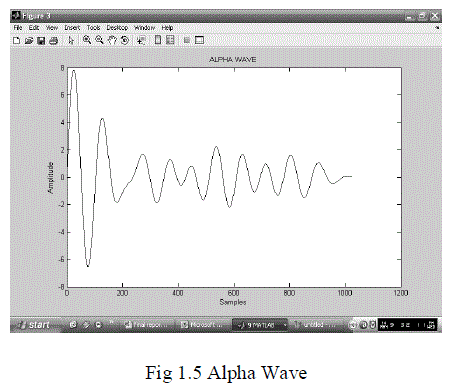 |
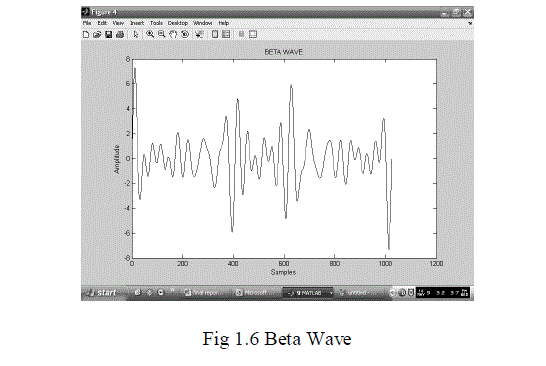 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
CONCLUSION |
| It was shown that the best basis selection and optimization of the mother wavelet through parameterization lead to improvement of performance in signal compression with respect to random selection of the mother wavelet and DWT. The method provides an adaptive approach for optimal signal representation for the purpose of compression and can thus be applied to any type of one-dimensional biomedical signal.A classical approach for optimizing the basis function set is to search for the best wavelet packet decomposition. The two optimizations (tree in wavelet packet decomposition and mother wavelet)can be merged in future studies. |
References |
|