Keywords
|
| Complex dynamics,Relative Superior Julia set, Relative Superior Mandelbrot set. |
INTRODUCTION
|
| A Fractal is a mathematical set that has a fractal dimension that usually exceeds its topological dimensions and may fall between the integers. In other words, Fractals may be described as self-similar patterns. As mathematical equations, fractals are usually nowhere differentiable, which illustrates that it cannot be measured in traditional ways. The term Fractal was first used by mathematician Benoit Mandelbrot in 1975. Mandelbrot based it on the Latin word” fractus”, that means broken or fractured. He used it to extend the concept of theoretical fractional dimensions to geometric patterns in nature. The history of fractal straces a path from chiefly theoretical studies to modern applications in computer graphics,with several notable people contributing canonical fractal forms along the way. |
| The study of transcendental function has emerged out as discrete dynamical systems in numerical and complex analysis. It forms a rich dynamics for well-known Julia sets and Mandelbrot sets[8]. On the other hand, the dynamics of iterated polynomials are one of the greatest pioneering work of Doaudy and Hubbard[10]. Given a polynomial of degree n? 2 the most important set is the Julia set J consisting of the points z ?C which have no neighborhood in family of iterates, forms a normal family. Specially for the polynomials, one can start with the set of points I which converge to infinity under iteration (escaping points) and its complement K ?C / I is known as filled in Julia sets and it consists of points with bounded orbits. In other words, the Julia set c J of the function c Q where 2 c Q ? z ? c is either totally disconnected or connected. Its counterpart, Mandelbrot set for a family c Q is defined as { : 0 } c c M ? c?C orbit of under iteration by Q is bounded For | c | ? 2, orbit of 0 escapes to? so only| c | ? 2 is considered. For any n, ( ) | (0) | 2 n c Q ? , then the orbit of 0 tends to infinity[8]. |
| The key feature of this paper is to show that the inverse sine function, which falls under category of transcendental function, is an example, where Julia set is all ofC . There is a great difference between the dynamics of polynomials and transcendental functions. Picard’s Theorem [21] tells us that for a transcendental function f ,given any “neighborhood of infinity” U ?[{z;| z |?r}, r?R] f (U) covers C with exception of at most one point. This is certainly not true for polynomials because we find a neighborhood of U so that f (U)? U . |
| The study of dynamical behavior of the transcendental functions were initiated by Fatou[12]. For transcendental function, points with unbounded orbits are not in Fatou sets but they must lie in Julia sets. Attractive points of a function have a basin of attraction, which may be disconnected. A point z in Julia for cosine function has an orbit that satisfies | Imz |?50 |
| A Julia set thus, satisfies the following properties: |
| (i) Closed |
| (ii) Nonempty |
| (iii) Forward invariant t(If z?J (F) , |
| then F(z)?J (F) , where F is the function). |
| (iv) Backward invariant |
| (v) Equal to the closure of the set of repelling cycles of F . |
| On the other hand, Fatou Set is the complement set of Julia set, also stated as stable set. Attracting cycles and their basins of attraction lie in the Fatou set, since iterates here tend to cycle and thus forms a normal family. |
| Thus, the iteration of complex analytic function F decompose the complex plane into two disjoint sets |
| 1. Stable Fatou sets in which iterates are well behaved. |
| 2. Julia sets on which the map is chaotic. |
| In trigonometric function, S(z) ? sin z , 0 is defined as fixed point for S . If 0x ?R , then either 0 S(x ) ? 0 or 0 ( ) 0 n S x ? . Also, we have the points lying on the imaginary axis have their orbits that tend to infinity since sin(iy) ? i sin(hy) . On the other hand for cosine function, if [ ( )] n C z ? ? ? as n ? ? , then orbits which escapes do so, with the increase in the imaginary part. Here, Mandelbrot plane will contain infinitely many critical points given by 2 2 n ? , where n?N . Sine and cosine functions are thus declared as “Topologically complete” [15]. |
| The dynamics of cosine and sine function as revealed in the past literature states that the points that converge to ? under iteration are organized in the form of rays. It is well known that the set of escaping points is an open neighbourhood of ? , which can be parameterized by dynamic rays. As the tangent function is compromised of sine and cosine function, thus it will undertake most of the properties of both the functions. For the entire transcendental functions, the point ? is an essential singularity (rather than super attracting point). Ereneko[11] studied that for every entire transcendental functions, the set of escaping points is always non-empty. His query was answered in an affirmative way by R. L. Devaney[5,6 &7], for the special case of Exponential function, where every escaping point can be connected to ? , along with unique curve running entirely through the escaping points. |
| A dynamic ray is connected component of escaping set, removing the landing points. It turns out to be union of all uncountable many dynamic rays, having Hausdroff dimension equal to one. However by a result of McMullen[15 ] the set of escaping points of a cosine family has an infinite planar Lesbegue measure. Therefore the entire measure of escaping points sits in the landing points of those rays which land at the escaping points |
| We are introducing in this paper dynamics of inverse sine function and applied Relative Superior Ishikawa iterates to develop an entirely new class of fractal images of this transcendental function. Escape criteria of polynomials are used to generate Relative Superior Mandelbrot Sets and Relative Superior Julia Sets. Our results are quite different from existing results in literature as we determined the connectivity of the Julia Sets using Ishikawa iterates. |
II. PRELIMINARIES
|
| The process of generating fractal images from sin( ) n z?arc z ?c is similar to the one employed for the self-squared function[17]. Briefly, this process consists of iterating this function up to N times. Starting from a value 0 z we obtain 1, 2, 3, 4, z z z z ... by applying the transformation tan( ) n z? z ? c . |
| Definition2.1: Ishikawa Iteration [13]: Let X be a subset of real or complex numbers and f : X ?X for 0x ?X , we have the sequences{ } n x and { } n y in X in the following manner: |
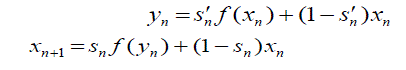 where 0 ? sn? ?1, 0 1 n ? s ? and ? ? n s? &? ? n s are both convergent to non zero number. where 0 ? sn? ?1, 0 1 n ? s ? and ? ? n s? &? ? n s are both convergent to non zero number. |
| Definition 2.2[4, 18]: The sequences? ? n x and ? ? n y constructed above is called Ishikawa sequences of iterations or Relative Superior sequences of iterates. We denote it by 0 ( , , , ) n n RSO x s s? t . Notice that 0 ( , , , ) n n RSO x s s? t with n s? =1 is 0 ( , , ) n SO x s t i.e. Mann’s orbit and if we place 1 n n s ? s? ? then 0 ( , , , ) n n RSO x s s? t reduces to 0 O(x , t) . |
| We remark that Ishikawa orbit 0 ( , , , ) n n RSO x s s? t with 1/ 2 n s? ? is relative superior orbit. Now we define Mandelbrot sets for function with respect to Ishikawa iterates. We call them as Relative Superior Mandelbrot sets. |
| Definition 2.3[4, 18]: Relative Superior Mandelbrot set RSM for the function of the form ( ) n c Q z ? z ? cwhere n = 1, 2, 3, 4… is defined as the collection of c?C for which the orbit of 0 is bounded i.e. { : (0) : 0,1, 2...} k c RSM ? c?C Q k ? is bounded. |
| In functional dynamics, we have existence of two different types of points. Points that leave the interval after a finite number are in stable set of infinity. Points that never leave the interval after any number of iterations have bounded orbits. So, an orbit is bounded if there exists a positive real number, such that the modulus of every point in the orbit is less than this number. |
| The collection of points that are bounded, i.e. there exists M, such that | ( ) | n Q z ?M , for all n, is called as a prisoner set while the collection of points that are in the stable set of infinity is called the escape set. Hence, the boundary of the prisoner set is simultaneously the boundary of escape set and that is Julia set for Q. |
| Definition 2.4[4, 18]]: The set of points RSK whose orbits are bounded under relative superior iteration of the function Q (z) is called Relative Superior Julia sets. Relative Superior Julia set of Q is boundary of Julia set RSK |
III. GENERATING THE FRACTALS
|
| We have used in this paper escape time criteria of Relative Superior Ishikawa iterates for function |
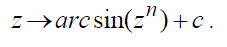 |
| Escape Criterion for Quadratics: Suppose that | z |? max{| c |,2 / s,2 / s?}, then | | (1 ) | | n nz ? ?? z and | | n z ? ? as n??.So, | z |? | c | &| z |?2 / s as well as | z |?2 / s? shows the escape criteria for quadratics |
| Escape Criterion for Cubics: Suppose 1/2 1/2 | z |? max{| b |, (| a | ?2 / s) , (| a | ?2 / s?) } then| | n z ? ? as n ? ? . This gives an escape criterion for cubic polynomials |
| General Escape Criterion: Consider 1/ 1/ | | max{| |, (2 / ) , (2 / ) } n n z ? c s s? then| | n z ? ? as n ? ? is the escape criterion. (Escape Criterion derived in [4,18]). |
| Note that the initial value 0 z should be infinity, since infinity is the critical point of tan( ) n z? z ? c . However instead of starting with 0 z = infinity, it is simpler to start with 1 z = c , which yields the same result. (A critical point of z ?F(z) ? c is a point where F?(z) ? 0 ). |
IV. GEOMETRY OF RELATIVE SUPERIOR MANDELBROT SETS AND RELATIVE SUPERIOR JULIA SETS
|
| The fractals generated from the equation sin( ) n z?arc z ?c possesses symmetry along the real axis. |
Relative Superior Mandelbrot Sets:
|
| ? In case of quadratic polynomial, the central body is bifurcated from middle. The body is maintaining symmetry along the real axis. Secondary lobes are very small initially for s = 1, s? =1. As the value of the set changes to s =0.8, s? =0.3, the central body gets more unified. As the value of s is still more minimized along with s? , the central body is merged into one with none of the secondary lobe. The symmetry is maintained along real axis. |
| ? In case of Cubic polynomial, the central body is showing bifurcation into two equal parts, each part containing one major secondary lobe which appears to be similar in size of central body. The symmetry of this body is maintained along both axes. For s =0.7 s? =0.3, the central body remains unaltered while the major secondary lobes gets more flattened and distorted, on each side. |
| ? In case of Biquadratic polynomial, the central body is divided into three parts, each part having one major secondary bulb. The secondary bulbs present on either side of the real axis shows larger extensions. The body is maintaining symmetry along the real axis. For s =0.6 s? =0.3, the major secondary lobes disappears. For s =0.6 s? =0.3, along the sides of two bifurcations of the central lobe, we observe extensions. |
| ? For n = 11, the body is showing ten bifurcations of the central body along with the beautiful ring shaped extensions along the imaginary axis. |
Relative Superior Julia Sets:
|
| ? Relative Superior Julia Sets for the transcendental arc sine function maintains its symmetry along axis, for quadratic polynomial. |
| ? The Relative Superior Julia Sets for Cubic function are symmetrical about both the axes i.e. along real and imaginary axes as well as possesses reflectional and rotational symmetry. |
| ? The Relative Superior Julia Sets for Biquadractic function is having symmetry along the real axis, along with a black central escape region, which resembles to its Mandelbrot sets. |
V. GENERATION OF RELATIVE SUPERIOR MANDELBROT SETS
|
| A. Mandelbrot Sets of Quadratic function: |
| Fig1:Relative Superior Mandelbrot Setfors=s'=1 |
 |
| Fig2:Relative Superior Mandelbrot Setfors=0.8, s'=0.3 |
 |
| Fig 3:Relative Superior Mandelbrot Setfor s=0.9, s'=0.1 |
 |
B. Mandelbrot Sets of Cubic function:
|
| Fig1:Relative Superior Mandelbrot Setfor s=s'=1 |
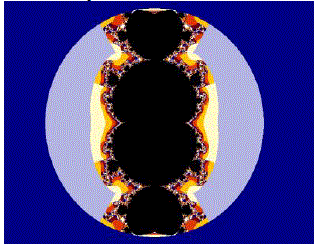 |
| Fig2: Relative Superior Mandelbrot Setfor s=0.7, s'=0.3 |
 |
| Fig 3:Relative Superior Mandelbrot Setfor s=0.8, s'=0.1 |
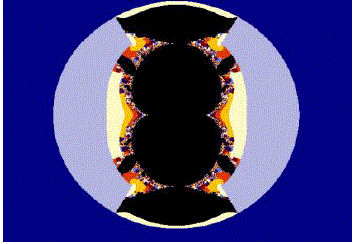 |
| C. Mandelbrot Sets of Biquadratic function: |
| Fig1:Relative Superior Mandelbrot Setfor s=s'=1 |
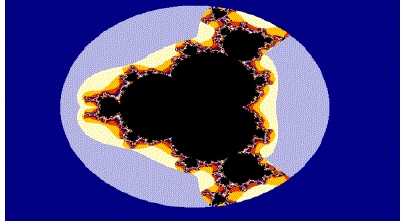 |
| Fig2: Relative Superior Mandelbrot Setfor s=0.6, s'=0.3 |
 |
| Fig 3: Relative Superior Mandelbrot Set for s=0.8, s'=0.1 |
 |
| D. Generalization of Relative Superior Mandelbrot Set |
| Fig1:Relative Superior Mandelbrot Setfor s=0.8, s'=0.1, n=11 |
 |
VI. GENERATION OF RELATIVE SUPERIOR JULIA SETS
|
A. Julia sets of Quadratic function:
|
| Fig1:Relative Superior Julia Setfor s=0.9, s'=0.1,c=-0.51250+.0125i |
 |
| B. Julia Sets of Cubic function: |
| Fig1:Relative Superior Julia Setfor s=0.7, s'=0.3, c= -0.0094170316490+.03114228566i |
 |
| C. Julia Sets of Biquadratic function: |
| Fig1:Relative Superior Julia Setfor s=0.8, s'=0.1,c=0.1476620813-0.01528084713i |
 |
VII. FIXED POINTS
|
A. Fixedpointsofquadraticpolynomial
|
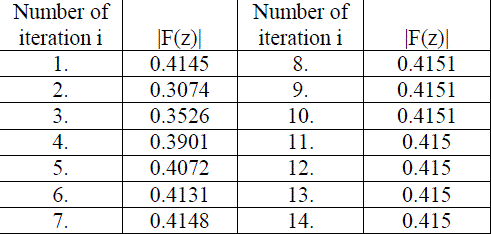 |
| Here we observed that the value converges to a fixed point after 11 iterations |
 |
| Here we observed that the value converges to a fixed point after 19 iterations |
 |
| Here we observed that the value converges to a fixed point after 19 iterations |
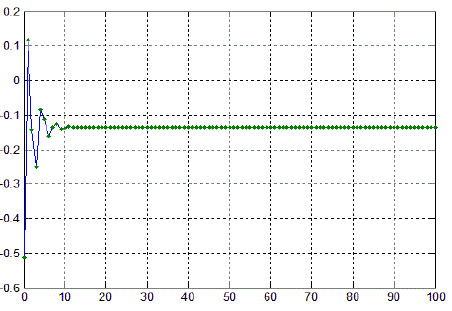 |
| B. Fixedpointsofcubicpolynomial |
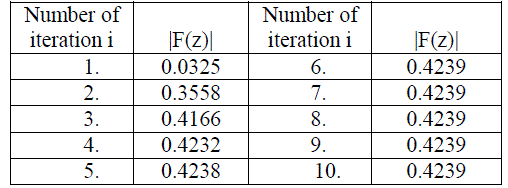 |
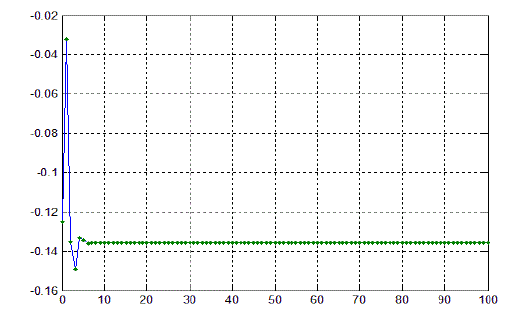
| Here we observed that the value converges to a fixed point after 06iterations |
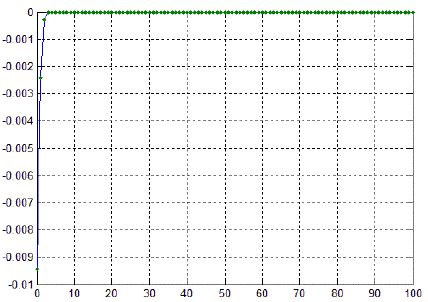
| Figure 1. Orbit of F(z) at s=0.8 and s'=0.1 for (z0= 0.02577277309+0.03516014432i) |
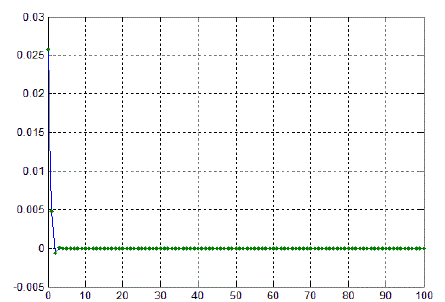 |
| Table 2: Orbit of F(z) at s=0.7 and s'=0.3 for(z0 =-0.0094170316490+.03114228566i) |
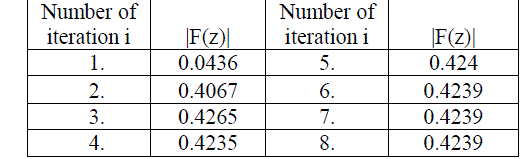 |
| Here we observed that the value converges to a fixed point after 06iterations |
| Figure 2. Orbit of F(z) at s=0.7 and s'=0.3 for(z0 =-0.0094170316490+.03114228566i) |
 |
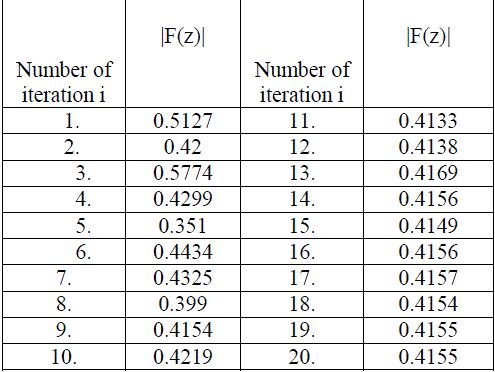
| C. FixedpointsofBiquadraticpolynomial: |
| Table 1: Orbit of F(z) at s=0.1 and s'=0.5 for (z0= 0.3000244068+0.1862906688 i) |
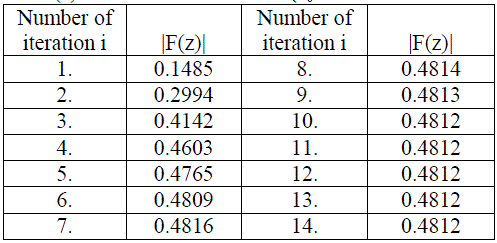 |
| Here we observed that the value converges to a fixed point after 10 iterations |
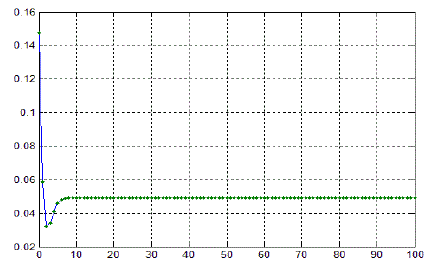
| Figure 1. Orbit of F(z) at s=0.6 and s'=0.3 for (z0= 0.1476620813 -0.01528084713i) |
 |
| Table 2 Orbit of F(z) at s=0.8 and s'=0.1 for (z0=0.1476620813 -0.01528084713i) |
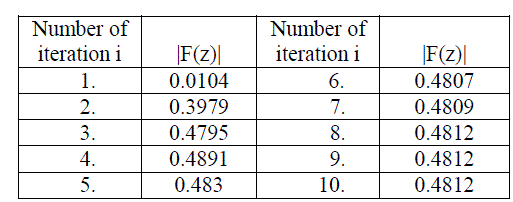 |
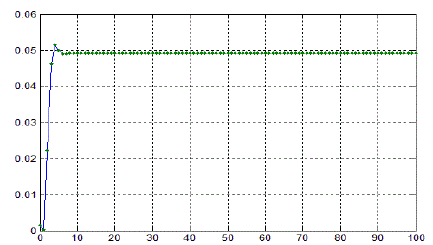
| Here observe that the value converges to a fixed point after 08 iterations |
| Figure 2. Orbit of F(z) at s=0.8 and s'=0.1 for (z0=0.1476620813 -0.01528084713i) |
 |
VIII. CONCLUSION
|
| In this paper we studied the inverse sine function which is one of the members of transcendental family. Relative Superior Mandelbrot sets possess 2n wings. Besides this, these Julia sets explores the presence of central black region, which are the Mandelbrot images of respective sets. For even powers, Relative Superior Mandelbrot sets show symmetry only along the real axis while on the other hand, for odd terms, body maintains its symmetry along both axes. The results thus obtained are innovative. Our study is unique in sense that we have used escape time criteria for transcendental function to generate fractals using Relative Superior Ishikawa iterates, otherwise results according to past literature would have shown Julia sets to be disconnected. |
References
|
- W. Bergweiler, Iteration of meromorphic functions. Bull. Amer. Math. Soc. (N. S.) 29 (1993), 151–188.
- W. Bergweiler and A Ereneko, “Dynamics of a higher dimensional analog of the trigonometric functions”, Bull. Amer. Math. Soc. (N. S.)1(2010), 35-38.
- B. Branner, The Mandelbrot Set, Proceedings of Symposia in Applied Mathematics39 (1989), 75-105. Published as Chaos and Fractals: TheMathematicsBehind the ComputerGraphics.
- Yashwant S Chauhan, RajeshriRana and Ashish Negi. “New Julia Sets of Ishikawa Iterates”, International Journal of Computer Applications7(13):34–42, October 2010. Published By Foundation of Computer Science.ISBN: 978-93-80746-97-5.
- R. L. Devaney and M. Krych, “Dynamics of exp(z)”, Ergodic Theory Dynam. Systems4 (1984), 35–52.
- Robert L. Devaney, FolkertTangerman, “ Dynamics of entire functionsnear the essential singularity”, Ergodic Theory and DynamicalSystems 64 (1986) 489–503.
- R. L. Devaney and F. Tangerman, “Dynamics of entire functions near the essentialSingularity”, Ergodic Theory Dynam. Systems 6 (1986),489–503.
- Robert L. Devaney, “An Introduction to Chaotic Dynamical Systems”, Second Edition, 1989, Perseus Books Publishing, Reading, MA.
- Robert L. Devaney, Xavier Jarque, and M´onica Moreno Rocha, “Indecomposable continua andMisiurewicz points in exponential dynamics”,Internat. J. Bifur. Chaos Appl. Sci. Engrg.15(2005), no. 10, 3281–3293.
- AdrienDouady and John Hubbard, “Etude dynamique des polynˆomes complexes”, Pr´epublicationsmath´ematiques d’Orsay 2 (1984) and 4(1985).
- AEreneko, “Iteration of entire functions”, Dynamical Systems and Ergodic theory, BanachCenter Publ. 23, Polish Sc. Pub. , Warsaw 1989,339-345.
- Pierre Fatou, “Sur Iteration des functions transcendantesentires”, Acta Math 47(1926), 337-378.
- S.Ishikawa,“Fixedpointsbyanew iteration method”,Proc.Amer.Math.Soc.44(1974),147-150.
- B. B. Mandelbrot, “ TheFractalGeometry of Nature”,W.H.Freeman,NewYork,1983.
- Curt McMullen, “Area and Hausdorff dimension of Julia sets of entire functions”, Transactions of the American Mathematical Society 300 1(1987), 329–342.
- J. Milnor, “Dynamics in One Complex Variable: Third Edition”, Princeton University Press, 2006.
- H. PeitgenandP.H.Richter, The Beautyof Fractals,Springer-Verlag,Berlin,1986.
- RajeshriRana, Yashwant S Chauhan and Ashish Negi. “Non Linear Dynamics of Ishikawa Iteration”, International Journal of ComputerApplications 7(13):43–49, October 2010. Published By Foundation of Computer Science.ISBN: 978-93-80746-97-5.
- RajeshriRana, Yashwant S Chauhan and Ashish Negi. “Ishikawa Iterates for Logarithmic Function”, International Journal of Computer
- Applications 15(5):47-56, February 2011. Published By Foundation of Computer Science. ISBN: 978-93-80747-50-1.
- G. Rottenfuser and D. Schleicher, “Escaping points of the cosine family”, ArXIV Math. DS/0403012 (2004)
- D. Schleicher, “The dynamical fine structure of iterated cosine maps and a dimension Paradox”, Duke Math. J. 136 (2007), 343–356.
- DierkSchleicher and Johannes Zimmer, “Escaping Points of Exponential Maps”, Journal of the London Mathematical Society (2) 67(2003),380–400.
- DierkSchleicher and JohannesZimmer, “Periodic Points and Dynamic Rays of Exponential Maps”AnnalesAcademiaeScientiarumFennicae28 2 (2003), 327–354.
|