Genetic Algorithm based controller design for a higher order process

Abstract

This Paper deals with the tuning of PID controller using conventional methods and computational technique like Genetic Algorithm. The main objective is to prove that the response of the system obtained is more desirable and satisfactory when the PID controller is tuned using Genetic Algorithm than when tuned using traditional methods. The obtained value is compared with conventional methods like Ziegler Nicholas and Tyreus Luyben methods. The criteria used for comparison include time domain specifications, Performance index and robustness of the system.

Keywords

PID tuning, Computational technique, GA, ZN, TL, PI, Controller

INTRODUCTION

Increasing complexities in industrial processes have compelled the control engineers to implement advanced control strategies to improve the efficiency of the process control system. Usage of PID controllers has become indispensible for its simplicity, reliability and flexibility [1]. The proportional term in the controller generally helps in establishing system stability and improving the transient response while the derivative term is often used when it is necessary to improve the closed loop response speed even further. Conceptually the effect of the derivative term is to feed information on the rate of change of the measured variable into the controller action. The most important term in the controller is the integrator term that introduces a pole at s = 0 in the forward loop of the process [5]. This makes the compensated open loop system a type 1 system for perfect steady state set point tracking. Technically, a PID controller reduces the steady state error, minimizes the overshoot and improves the settling rate [6]. They do, however, present some challenges to control and instrumentation engineers in the aspect of tuning of the gains required for stability and good transient performance [5]. These features can be attained only by proper tuning of the PID controller. Various tuning algorithms were proposed by many scientists- each algorithm having its own merits and demerits. PID controller is tuned using the algorithm which is suitable for that particular process. Well known and widely implemented algorithms include ZN tuning, Cohen-Coon method, Tyreus Luyben technique and Internal model controller. ZN method was proposed by John G. Ziegler and Nathaniel B. Nichols in 1942 [5]. ZN method is one of the most widely used tuning techniques as it involves simple algorithm for its implementation. The Cohen-Coon method of controller tuning corrects the slow, steady-state response given by the Ziegler-Nichols method when there is a large dead time (process delay) relative to the open loop time constant; a large process delay is necessary to make this method practical because otherwise unreasonably large controller gains will be predicted. This method is only used for first-order models with time delay; due to the fact that the controller does not instantaneously respond to the disturbance. IMC was introduced by Garcia and Morari in the year 1982 [2]. Design of IMC based controller depends on the complexity of the model and the performance requirements stated by the designer. The proposed IMC structure provides valuable insight regarding controller tuning effects on both performance and robustness. Literature Survey: The research work of Stark in finding the mathematical model of the control system responsible for opening and closing of pupil according to the intensity of light entering the human eye in used in this paper. His work is taken from the book named Control and dynamical systems by Richard M. Murray. The controller of the system is tuned using both conventional and advanced tuning strategies. The basic techniques implemented in controlling the process using Genetic Algorithm are taken from “Application of Genetic Algorithm for tuning of PID Controller for a real time industrial process”.

II. SYSTEM DESCRIPTION

The human eye is an organ that is easily accessible for experiments. It has a control system which adjusts the pupil opening to regulate the light intensity at the retina. This control system was explored extensively by Stark in the late 1960s [4]. To determine the dynamics, light intensity on the eye was varied sinusoidally and the pupil opening was measured. A fundamental difficulty is that the closed loop system is insensitive to internal system parameters. Analysis of a closed loop system thus gives little information about the internal properties of the system. Stark used a clever experimental technique which allowed him to investigate both open and closed loop dynamics. He excited the system by varying the intensity of a light beam focused on the eye and he measured pupil area. By using a wide light beam that covers the whole pupil, the measurement gives the closed loop dynamics. The open loop dynamics was obtained by using a narrow beam. By focusing a narrow beam on the edge of the pupil opening the gain of the system can be increased so that the pupil oscillates.

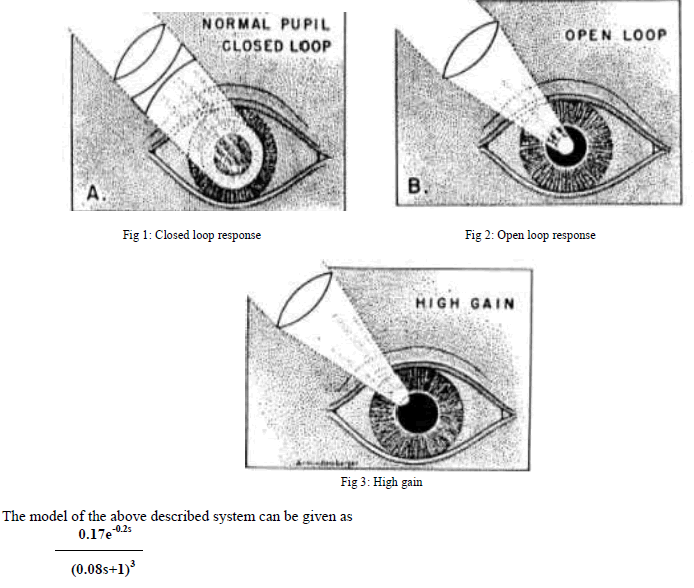III. CONVENTIONAL TUNING METHODS

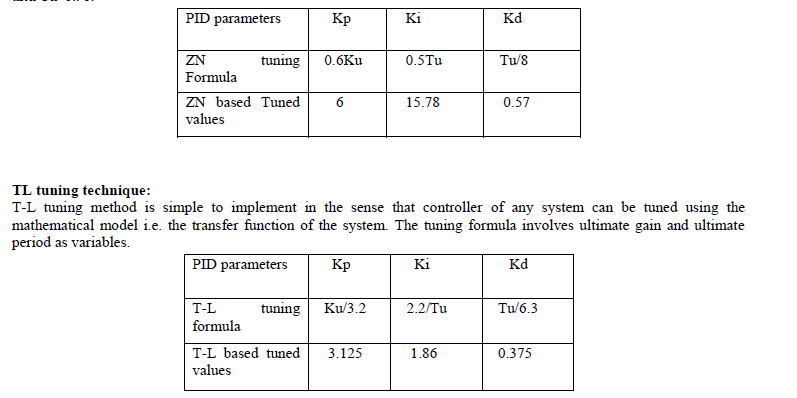
A suitable PID controller should be included in the process control loop to improve the response of the system. ZN and Tyreus- Luyben techniques were proven to be the suitable techniques for tuning a higher order process. ZN tuning technique: Tuning a controller using ZN technique involves determining the values of ultimate gain (Ku) and ultimate period (Tu). These values were found using Bode plot and root locus. For ωco=8.26rad/sec, it is found that Ku=10 and Tu=0.76.

IV. GENETIC ALGORITHM

Genetic Algorithm form a class of adaptive heuristics, based on principles derived from the dynamics of natural genetics. The searching process simulates the natural evolution of biological creatures and turns out to be an intelligent exploitation of a random search. A candidate solution (chromosome) is represented by an appropriate sequence of numbers. In many applications the chromosome is simply a binary string of 0’s and 1’s. The quality of its fitness function evaluates a chromosome, with respect to the objective function of the optimization problem. A selected population of solution initially evolves by employing mechanisms modelled similar to those used in Genetics. Various operations are performed while tuning a controller with GA namely Reproduction, Crossover and Mutation. Reproduction Reproduction selects goods strings in a population and forms a mating pool known as selection operator. Here, Rank order method is used as reproduction operator where the probability of selecting a particular string is more if its fitness is more. Crossover Crossover involves creating new strings by exchanging information among strings of the mating pool based on a probability Pc. A string point crossover operator is used here which is performed randomly by choosing a crossing site along the string and by exchanging all bits on either side of the chosen site.

Mutation Mutation involves changing one particular bit of the selected string i.e. 1 is mutated into 0 and vice versa. The need for mutation is to create a point in the neighbour of the current point, thereby achieving a local search around the current solution. Mutation is also used to maintain diversity in the population. The controller can be tuned using Genetic Algorithm by assuming the following operators: Initial population size=100 Bounds of controller parameters: Kp = [0 8] Ki = [0 20] Kd = [0 2] Objective function: Integral of Absolute Error The implementation of GA is done to find the optimal PID controller parameters. They are plotted as the best values among the considered population size for all the iterations, and are given in the following figures:

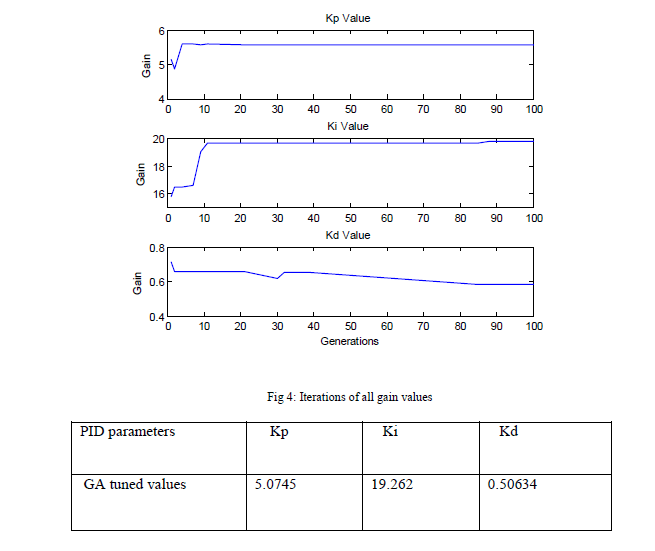V. RESULTS AND COMPARISON

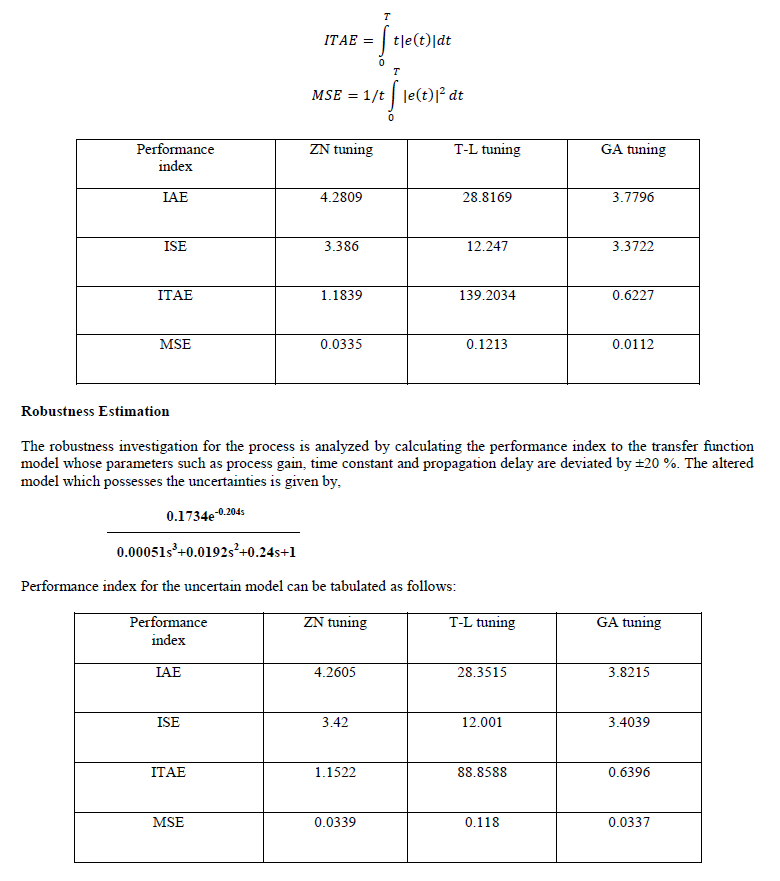
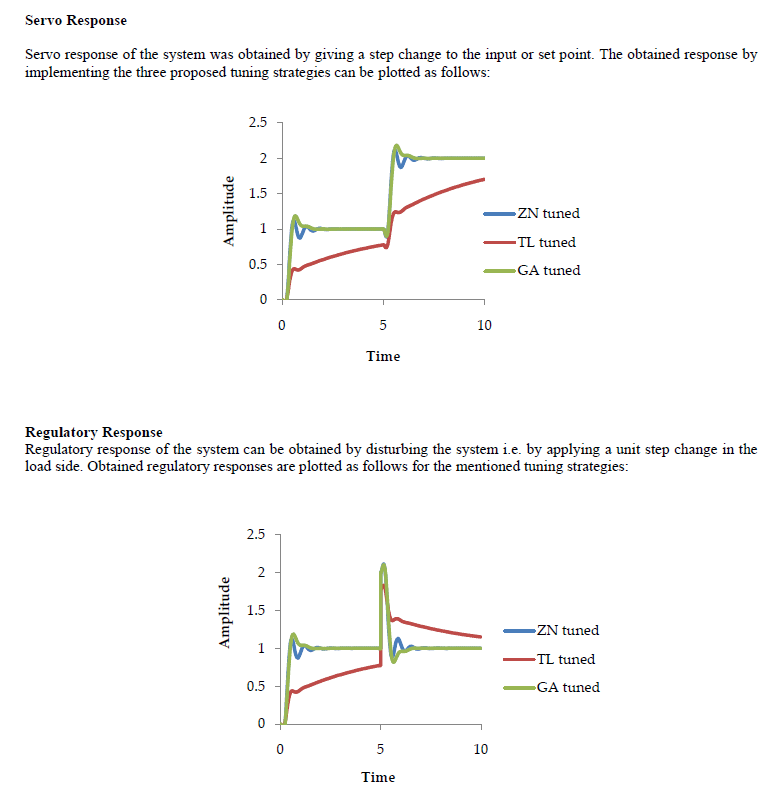
Response of the system was observed by applying a unit step input with a PID controller tuned using the proposed conventional methods and genetic algorithm. The following graph shows the comparative analysis of all the three methods:

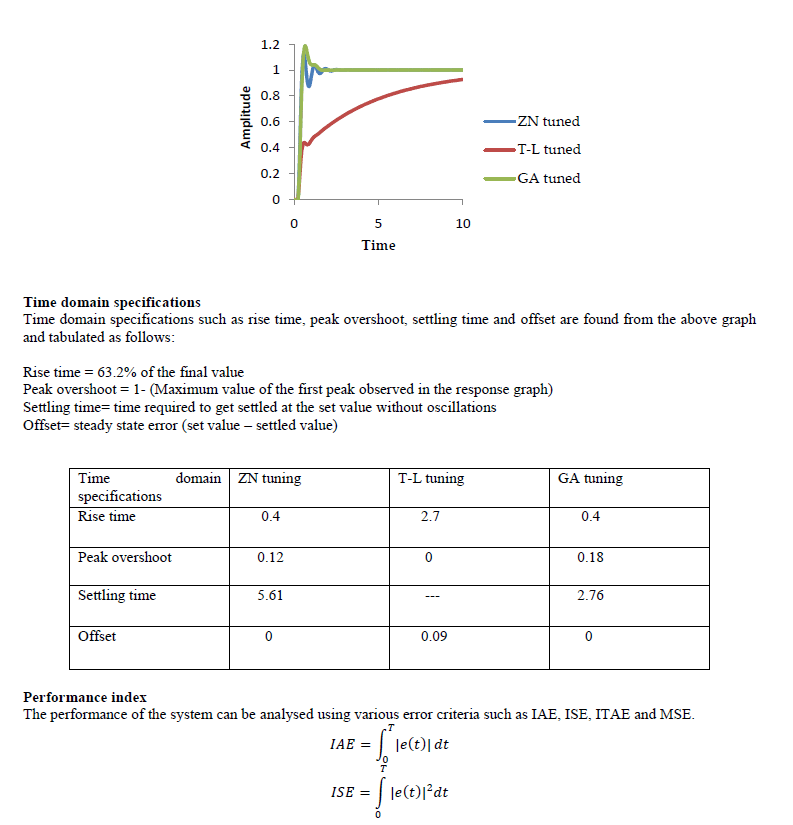VI. CONCLUSION

It is obvious from the presented results that the response of the system with a GA tuned PID controller significantly outmatches the responses of the system with conventionally tuned PID controllers. Rise time and settling time of the system is notably lower for a GA tuned controller than its conventional counterpart. The values of all errors are lower for a GA tuned controller. System with controller tuned using genetic algorithm is more robust for uncertain models. Better servo and regulatory responses are obtained if the controller is tuned using Genetic algorithm. The various results presented prove the betterness of the GA tuned PID settings than ZN and TL tuned ones. The simulation responses for the models reflect the effectiveness of the GA based controller in terms of time domain specifications. The performance index under the various error criterions for the proposed controller is always less than the conventionally tuned controller. GA presents multiple advantages to a designer by operating with a reduced number of design methods to establish the type of the controller, giving a possibility of configuring the dynamic behaviour of the control system with ease, starting the design with a reduced amount of information about the controller (type and allowable range of the parameters), but keeping sight of the behaviour of the control system.

References

1. [1]. S. M. Girirajkumar, Atal. A. Kumar, N. Anantharaman, Application of Genetic Algorithm for tuning of PID Controller for a real time industrial process, in sensors and Transducers Journal , Oct 2010.
2. Mohd Sazli Saad, Hishamuddin Jamaluddin, Intan Zaurah Mat Darus, Implementation of PID Controller Tuning using Differential Evolution and Genetic Algorithm, in International Journal of Innovative computing, Information and control, November 2012 .
3. Neenu Thomas, Dr. P. Poongodi, Position Control of DC Motor Using Genetic Algorithm Based PID Controller, in the Proceedings of the World Congress on Engineering 2009 Vol II.
4. Book named Control and dynamical systems by Richard M. Murray, Chapter 6 named Transfer Function.
5. Arturo Y. Jaen-Cuellar, Rene de J. Romero-Troncoso, Luis Morales-Vela Zquez and Roque A. Osornio-Rios, PID controller tuning optimization with Genetic Algorithm in Servo system, in International Journal of Advanced Robotic Systems, May 2013.
6. Aytekin B. Agis, Determination of the PID Controller Parameters by Modified Genetic Algorithm for Improved Performance, in the Journal of Information , Science and Engineering, 2007.