Governing Control and Excitation Control for Stability of Power System Based on ANFIS

Abstract

The issue of power system stability is becoming more crucial [1]. The excitation and governing control of generator play an important role in improving the dynamic and transient stability of power system. In this paper, the authors present a Neuro-fuzzy based method for the excitation control and governing control. The application of Neuro-fuzzy model (ANFIS model) to generate two compensating signal to modify the controls during system disturbances is proposed [5]. A simulation model comparing single machine to infinite bus system is applied [6]. The oscillation of internal generator angles is observed to indicate the good performance of proposed control scheme [8]. Power system stability issue has been studied widely. Many significant contributions have been made, not only in the aspect of analyzing and explaining the dynamic phenomena but also in the effort of improving the stability of transmission systems. Among these techniques, generator control is one of the most widely applied in power industry. In this paper a coordination of governing control and excitation control using Adaptive Neuro Fuzzy Inference System (ANFIS) model compensate their control inputs during faults [1]. The proposed ANFIS automatically coordinates the behavior of the two compensations. The observations show its satisfactory behavior for proposed control.

Keywords

Power System, Transient Stability, Fuzzy logic, Excitation and governing Control.

I.INTRODUCTION

Power system stability issue has been studied widely. Many significant contributions have been made, not only in the aspects of analyzing and explaining the dynamic phenomena, but also in the efforts of improving the stability of transmission systems [10]. Among these techniques, generator control is one of the most widely applied in the power industry [12]. This typically includes governing and excitation control. Most attention is directed toward the excitation control. Most of excitation controls are based on SISO-PID control, MIMO linear control, optimal linear and non-linear control, and intelligent control, such as applications of neural network and fuzzy logic and hybrid of these two i.e. neuro-fuzzy systems [13].

In the field power plant engineering fuzzy set theory is applied in system control, planning and load scheduling. The neural network has also been applied in power system control by developing neural controllers. Fuzzy logic has also been applied to design power system stabilizers. Governing system behavior is neglected in the design of excitation control. Part of the reason is the slow response of governing systems compared with exciting system [5]. However proper control of governing system is helpful in damping system oscillation and improving the transient stability [7-9].

In this piece of research work, coordination of governing control and excitation control using neuro-fuzzy theories to compensate their control inputs during faults. The angular speed ( ), the accelerating speed   m c P  P and the terminal voltage Vt  of generator are observed to characterize the severe ness of oscillation [2]. The design of Neuro-fuzzy controller is applied to a single machine infinite bus system [7]. A 3-phase fault is used as an example of system disturbances. SIMULINK simulation model is built to study the dynamic behavior of synchronous machine and the performance of proposed controller [11].

II.RELATED WORK

The reliability of a system can be determined on the basis of tests or the acquisition of operational data. However, due to the uncertainty and inaccuracy of this data, the estimation of precise values of probabilities is very difficult in many systems (e.g. power system, electrical machine, hardware etc., Hammer (2001), El-Hawary (2000)).

The basis for this approach is constituted by the fundamental works on fuzzy set theory of Zadeh (1978), Dubois and Prade (1980), Zimmerman (1986) and other. The theory of fuzzy reliability was proposed and development by several authors, Cai, Wen and Zhang (1991, 1993); Cai (1996); Chen, Mon (1993); Hammer (2001); El-Hawary (2000), Onisawa, Kacprzyk (1995); Utkin, Gurov (1995). The recent collection of papers by Onisawa and Kacprzyk (1995), gave 654 I.M. ALIEV, Z. KARA many different approach for fuzzy reliability. According to Cai, Wen and Zhang (1991, 1993); Cai (1996) various form of fuzzy reliability theories, including profust reliability theory Dobois, Prade (1980); Cai, Wen and Zhang (1993); Cai (1996); Chen, Mon (1993); Hammer (2001); El-Hawary (2000); Utkin, Gurov(1995), posbist reliability theory, Cai, Wen and Zhang (1991, 1993) and posfust reliability theory, can be considered by taking new assumptions, such as the possibility assumption, or the fuzzy state assumption, in place of the probability assumption or the binary state assumption. Chen [14] analyzed the fuzzy system reliability using vague set theory. The values of the membership and non-membership of an element, in a vague set, are represented by a real number in [0, 1]. Cai, Wen and Zhang (1993) presented a fuzzy set based approach to failure rate and reliability analysis, where profust failure rate is defined in the context of statistics. El-Nawary (2000) presented models for fuzzy power system reliability analysis, where the failure rate of a system is represented by a triangular fuzzy number. The work of Jerry M.Mendel and Feilong Liu (2007) on Super-Exponential Convergence of the Karnik–Mendel Algorithms for Computing the Centroid of an Interval Type-2 Fuzzy Set is a well-recognized work in the field. Design of Interval Type-2 Fuzzy Logic Based Power System Stabilizer (Imam Robandi, and Bedy Kharisma 2008) has sufficient materials as a reference work. Juan R. Castro and Oscar Castillo (2007) worked on Interval Type-2 Fuzzy Logic for Intelligent Control Applications. Also Jerry M. Mendel and Robert I.Bob John (2002) presented, how Type-2 Fuzzy Sets Made Simple. Mamdani ( 1974) developed the method to apply the fuzzy algorithm for simple control of dynamic plant. Qureshi (2003) published his work on power system reliability problems, control problems and protection problems. Qureshi (2004) in his Ph.D. thesis took the project work of Reliability of nuclear plants using fuzzy logic transformation. R.R.Yager(2000) reported a valuable information on fuzzy subsets of type-2 in decision. N.N.Karnik and J.M. Mendel worked on interval type-2 fuzzy logic systems and reported his findings in IEEE Transactions, fuzzy systems.

III. NEURO-FUZZY CONTROL DESIGN.

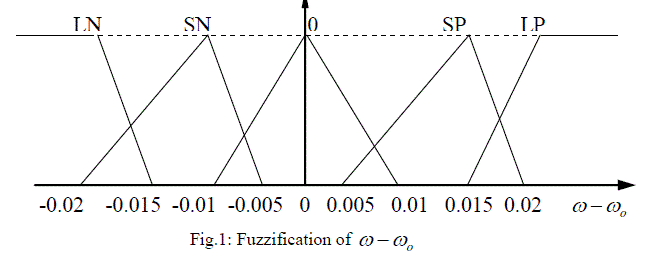
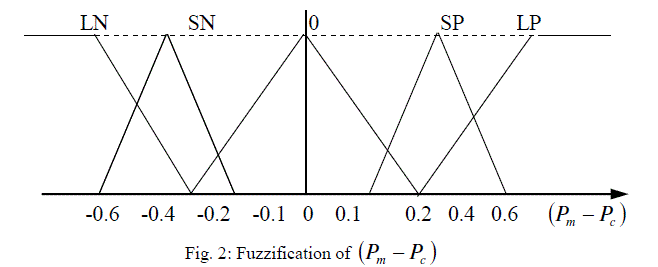
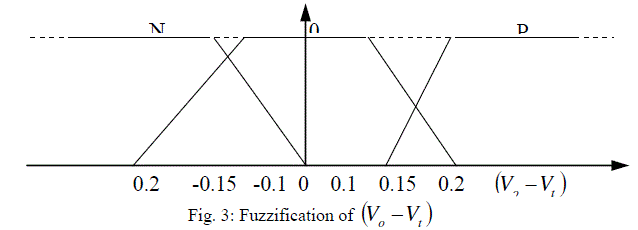
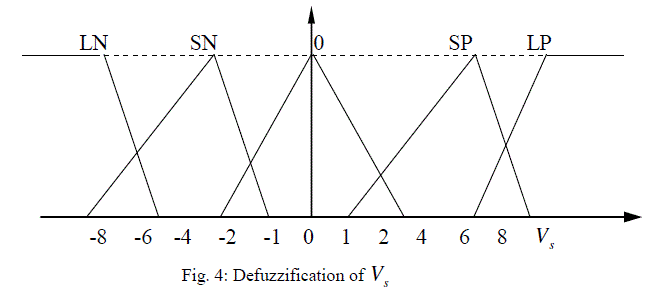
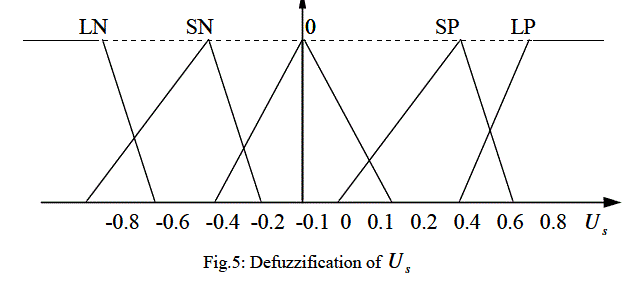
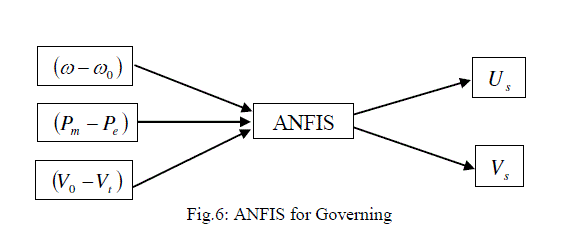
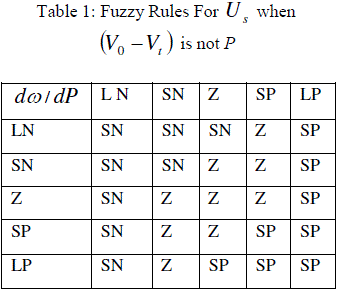
The basic dynamic behavior of a generator can be shown using a simple single machine to infinite bus system. In proposed study, the control scheme was designed for the single generator11. The governing control is a traditional PID Control, which is similar to International Journal of Electrical and Electronics Engineering (IEEE) type 1 model. The excitation control is a ANFIS architecture. Fig.1 to Fig.3 shows the fuzzification of input parameters i.e. incremental angular speed, power and terminal voltage respectively. Similarly Fig.4 & Fig.5 shows the output parameters i.e. source voltage and command signal respectively [1-3].

IV. DESIGN OF ANFIS COMPENSATION MODEL

Two performance indices (i) oscillating time or system damping should be faster, (ii) transfer capability, the more power transferred, the better are performances demonstrated here. In a single machine to infinite bus system, the power output of generator can be expressed as [13].

(3)

When there is fault in the transmission line as shown in fig7. The machine is running along the curve II during the fault period. When the fault disappears, the machine will run along the curve I . Area A represent the accelerating energy and B the decelerating energy. For damping A and B must be smaller. For this either the mechanical power input ( Pm) is reduced or electric power output ( Pe) is increased [8,12].

After increasing the voltage and decreasing the mechanical power follow first swing the same behavior as mentioned above when machine is in acceleration and decreasing the voltage and increasing the mechanical power when machine is in deceleration. These behaviors are shown in fig.8 and fig.9. Considering the slow reaction of governing system, two compensating signals Us and Vs are generated by ANFIS loop [1].

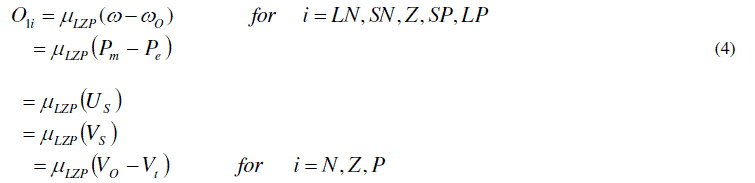V. SIMULATION RESULTS

In the simulation, the performance of the controllers with and without compensations is verified. In three phase fault occurs at t = 2.0 second at the beginning of one line and last for 0.2 second. By comparing the oscillation of internal angle  of generator for fault at the end of transmission line in two cases, with and without Fuzzy Logic compensation, as shown in fig. 11, the oscillation of  in the case with compensation is damped faster then that without compensation [14].

Similarly fig.12, fig.13 and fig.14 show the comparison of oscillation of internal angle of generator with fault at middle, beginning and generalized form of transmission line for two cases i.e. with ANFIS compensation and without ANFIS compensation. The dotted line curve shows the response of damping without ANFIS compensation and solid curve shows the response of damping with ANFIS compensation. Also some other cases were simulated to check the performance of proposed compensating, including the single line to ground, double line to ground and line-to-line faults, loud jumps.

VI. DISCUSSION

The compensating signal s U for governor generated by ANFIS block and the generated compensating signal s V for the conventional control (linear optimal excitation control) are referred as the control with ANFIS compensation and without ANFIS compensation respectively. By comparing the oscillation of internal angle  of generator in two cases, with and without ANFIS compensation as shown in fig.14, the oscillation of  in the case with compensation is damped out faster than without compensation.

The transient stability of transmission line is compared here. Three-phase fault in beginning of transmission is used as an example. Table 3 and 4 are showing the parameters of governing system and the parameters of modeled system respectively.

The robustness of compensated control is studied in simulation. The severe ness of system faults is simulated by the faults at different positions in the transmission line. The fault at the beginning, in the middle and at the end of transmission line is studied. It can be observed that the proposed compensation is robust for various system faults. In serious in slide system faults cases the compensation helps the original controls to damp the system oscillation. When the disturbances are trivial, which won’t cause large oscillation, as designed, there are no compensating outputs.

The cases with only one compensating output are also studied. When only the output for exciting control is added, the control performance is better than that without compensation except the first swing. When only the output for governing control is added the first swing is better but those after first swings are worse than the oscillation in the case without compensation.

VII. CONCLUSION

The generator controls are investigated in a single machine to infinite bus system. By analyzing the dynamic behavior of synchronous machine, two compensating variables are introduced based on the ANFIS architecture[1,14]. Since both governing and exciting controls are compensated, the proposed ANFIS compensator coordinates the behaviors of two controls. The transient stability of the transmission line is also compared with and without compensation case

Table 5 shows about 4.6% increase of the transient stability [14]. The benefits came from the decrease of mechanical power and increase of the voltage after fault disappeared in first swing [1,11]. The robustness of the proposed control is studied .The compensated generator controls display good performance for different disturbance [1,14].

References

1. Jang J.S.R., Sum C.T. & Mizutani” Neuro-fuzzy and soft computing” A computational Approach to learning one machine Intelligence “ Prentice Hall India, New Delhi, 2004
2. Lu Qiang, Wang Zhonghong, Han Yingdo “Optimal Control of Power Transmission System”, Published in China, 1982.
3. Lu Qiang, Sun Yuanzhang “ Power System Nonlinear Control”, Published in China, 1993.
4. Taiyou Yong, Study of Large Generator Fast Valve Control and Fuzzy Control”, Master Thesis in Tsinghua University, 1995.
5. Hiyama T, “Rule-based stabilizer for multi-machine power system” IEEE Transactions on Power-System, Vol., no; p.403-11, 1990
6. Hsu Y.Y., Cheng CH,”A fuzzy controller for generator excitation control”, IEEE Transactions on System, Man and Cybernetics. Vol.23, no.2, pp 532-39, 1993.
7. EI-Metwally K.A.; Malik O.P., “Fuzzy logic power system stabilizer”, IEEE Proceeding Generation Transmission and Distribution. Vol.142, no.3, pp 277-81, 1995
8. Hiyama T “ Integrated fuzzy logic stabilizing controller for power systems” Proceeding of the 35th IEEE Conference on Decision and Control (Cat. No. 96CH35989) IEEE, York , NY, 4 vol.48 58 pp 2185-90 vol.2, USA; 1996
9. Toliyat H.A., Sadeh J., Ghazi R.“ Design of augmented fuzzy logic power systems stabilizers to enhance power systems stability”, IEEE Transactions on Energy Conversion.Vol.11, no1, pp97-103. 1996
10. Hiyama T,Ueki Y, Andou H,“ Integrated fuzzy logic generator controller for stability enhancement”, IEEE Transactions on Energy Conversion. Vol. 12, no.4, p.400-6, 1997
11. El-Sherbiny M.K., EL Saady G, “Efficient incremental fuzzy logic controller for power stabilization” Electric Machines and Power Systems. Vol.25, no.4, pp 429-41, 1997
12. Hiyama-T, “Damping of multi-mode oscillations using integrated fuzzy logic generator controller”, APSCOM-97. Fourth International Conference on Advances in Power System Control, Operation and Management (IEEE Conf. Publ. No.450). IEEE, London, UK, 2 vol. Xxiii+840, pp 77-82 vol.l. , 1997
13. Dash P.K., Liew A.C., Mishra B.R., “ An adaptive PID stabilizer for power systems using fuzzy logic” Electric Power Systems Research. Vol.44, no.3, p.213-22, 1998,
14. MATLAB Manual on SIMULINK, FUZZY