Research & Reviews: Journal of Engineering and Technology
MenuISSN: 2319-9873
ISSN: 2319-9873
+44 7456 035580 1Department of CSE, BVC Engineering College, Odelarevu, Andhra Pradesh, India
2Department of CSE, Acharya Nagarjuna University, Guntur, Andhra Pradesh, India
3Department of CSE, JNTUK, Kakinada, Andhra Pradesh, India
Received: 25/08/2013 Accepted: 01/10/2013
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
NLCA has grown as potential classifier for addressing major problems in bioinformatics. Lot of bioinformatics problems like predicting the protein coding region, finding the promoter region, prediction of the structure of protein and many other problems in bioinformatics can be addressed through Cellular Automata. Even though there are some prediction techniques addressing these problems, the approximate accuracy level is very less. An automated procedure was proposed with HACA (Hybrid Attractor Cellular Automata) which can address all these problems. Extensive experiments are conducted for reporting the accuracy of the proposed tool. The average accuracy of HACA when tested with ENCODE, BG570, HMR195, Fickett and Tongue, ASP67 datasets is 78%.
Abbreviations: Non Linear Cellular Automata(NLCA) ,Cellular Automata (CA), Hybrid Attractor Cellular Automata (HACA), Genetic Algorithm (GA)
Cellular Automata, HACA, Protein Structure, Promoter Region, Protein Coding Region
Many interesting problems in bioinformatics that can be addressed by Cellular Automata Classifier. Predicting the structure of protein with the topology of the chain, finding the protein coding region and finding the promoter region can be done very easily with NLCA. The tree dimensional arrangement of amino acid sequences can be described by tertiary structure. They can be predicted independent of each other. Functionality of the protein can be affected by the tertiary structure, topology and the tertiary structure. Structure aids in the identification of membrane proteins, location of binding sites and identification of homologous proteins [9-11] to list a few of the benefits, and thus highlighting the importance, of knowing this level of structure This is the reason why considerable efforts have been devoted in predicting the structure only. Knowing the structure of a protein is extremely important and can also greatly enhance the accuracy of tertiary structure prediction. Furthermore, proteins can be classified according to their structural elements, specifically their alpha helix and beta sheet content.
Proteins are chains of amino acids joined together by peptide bonds. Many conformations of this chain are possible due to the rotation of the chain about each Cα atom [12-15]. It is these conformational changes that are responsible for differences in the three dimensional structure of proteins. Each amino acid in the chain is polar, i.e. it has separated positive and negative charged regions with a free C=O group, which can act as hydrogen bond acceptor and an NH group, which can act as hydrogen bond donor. These groups can therefore interact in the protein structure. The 20 amino acids can be classified according to the chemistry of the side chain which also plays an important structural role. Glycine takes on a special position, as it has the smallest side chain, only one Hydrogen atom, and therefore can increase the local flexibility in the protein structure.
Gish et al has proposed database similarity search for identifying protein coding regions, Salzburg et al has proposed a decision tree algorithm to solve the problem. Very less work was done to find the promoter regions in DNA sequences. The Objective of structure prediction is to identify whether the amino acid residue of protein is in helix, strand or any other shape. In 1960 as a initiative step [25-27] of structure prediction the probability of respective structure element is calculated for each amino acid by taking single amino acid properties consideration [1,3,6]. The third generation technique includes machine learning, knowledge about proteins, several algorithms which gives 70% accuracy. Neural Networks [10,11] are also useful in implementing structure prediction programs like PHD, SAM-T99.
This model is built describing a predefined set of data classes. A sample set from the database, each member belonging to one of the predefined classes, is used to train the model. The training phase is termed as supervised learning of the classifier. Each member may have Hybrid features. The classifier is trained based on a specific metric. Subsequent to training, the model performs the task of prediction [28-30] in the testing phase. Prediction of the class of an input sample is done based on some metric, typically distance metric.
The evolution process is directed by the popular Genetic Algorithm (GA) [16,17] with the underlying philosophy of survival of the fittest gene. This GA framework can be adopted to arrive at the desired NLCA rule structure appropriate to model a physical system. The goals of GA formulation are to enhance the understanding of the ways NLCA performs computations and to learn how NLCA may be evolved to perform a specific computational task and to understand how evolution creates complex global behavior in a locally interconnected system of simple cells.
A NLCA consists of a number of cells organized in the form of a lattice. It evolves in discrete space and time. The next state of a cell depends on its own state and the states of its neighboring cells. In a 3-neighborhood dependency, the next state qi(t + 1) of a cell is assumed to be dependent [36] only on itself and on its two neighbors (left and right), and is denoted as
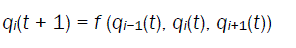(1)
where qi(t ) represents the state of the ith cell at tth instant of time, f is the next state function and referred to as the rule of the automata. The decimal equivalent of the next state function, as introduced by Wolfram, is the rule number of the NLCA cell. In a 2-state 3-neighborhood NLCA, there are total 223 that is, 256 distinct next state functions .Out of 256 rules, two rules 85 and 238 are illustrated below:
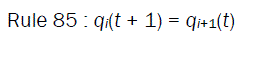(2)
(3)
An n-bit HACA with k-attractor basins can be viewed as a natural classifier. It classifies a given set of patterns into k number of distinct classes, each class containing the set of states in the attractor basin. To enhance the classification accuracy of the machine, most of the works have employed HACA Fig 1, to classify patterns into two classes (say I and II). The following example illustrates an HACA [31] based two class pattern classifier.
Figure 1: Example of HACA with basin 0000
Input : The Training set S = {S1, S2, · ·, SN}
Output : HACA Tree. Partition(S,N)
Step 1 : Generate a –spatial HACA with N number of attractor basins.
Step 2 : Distribute S based on fitness into N attractor basins (nodes).
Step 3 : Evaluate the distribution as per rule in each attractor basin
Step 4 : If S’ of an attractor basin belong to only one class, then label the attractor basin (leaf node) for that spatial class.
Step 5 : For examples (S’) of an attractor basin belong to N’ number of classes, then Partition (S’, N’).
Step 6 : Stop.
A class of non-linear CA, termed as Hybrid Attractor CA (HACA) [32], has been proposed to develop the model. Theoretical analysis, reported in this chapter, provides an estimate of the noise accommodating capability of the proposed HACA based associative memory model. Characterization of the basins [18] of attraction of the proposed model establishes the sparse network of non-linear CA ( HACA) [33,34] as a powerful pattern recognizer for memorizing unbiased patterns. It provides an efficient and cost-effective alternative to the dense network of neural net for pattern recognition. Detailed analysis of the HACA rule space establishes the fact that the rule subspace of the pattern recognizing/classifying NLCA lies at the edge of chaos. Such a NLCA, as projected in [20], is capable of executing complex computation. The analysis and experimental results reported in the current and next chapters confirm this viewpoint. A HACA employing the NLCA rules at the edge of chaos is capable of performing complex computation associated with pattern recognition.
The entropy and mutual information of the NLCA in successive generations of GA are reported in for four different NLCA size (n= 10, 15, 20, 30). For each of the cases, the values of entropy and mutual information reach their steady state once the AIS FHACA for a given pattern set gets evolved. For understanding the motion, the initial population (IP) is randomly generated. All these figures points to the fact that as the CA evolve towards the desired goal of maximum pattern recognizing capability, the entropy values fluctuate in the intermediate generations, but saturate to a particular value (close to the critical value 0·84 [24]) when fit rule is obtained. Simultaneously, the values of mutual information fluctuate at the intermediate points prior to reaching maximum value that remains stable in subsequent generations. All these figures indicate that the CA move from chaotic region to the edge of chaos to perform complex computation associated with pattern recognition.
Crossover operator randomly chooses a locus and exchanges the subsequences before and after that locus between two chromosomes to create two offspring. The crossover operator helps to explore the search space by virtue of providing means to generate new solutions out of the current population. The probability of selecting a pair of chromosomes to be employed for crossover depends upon the fitness of chromosomes. Majority of chromosomes for the next generations are produced through the crossover process. We have experimented with two different techniques of crossover to speed up the rate of convergence. However, there is no major difference in performance between the two schemes.
Figure 1: Score Analysis
Mutation operator randomly flips some of the bits in a chromosome. The mutation, applied to perturb one or more solutions, ensure that the search space explored is not closed under crossover. The probability of mutation on a given chromosome is kept very low. In our problem, 10% of the population of NP is generated out of mutations of the elite rules. Here also we have experimented with two standard techniques of mutation.
• Using Bp, create an input sequences Ib (corresponding to the base NLCA protein) by replacing each amino acid in the primary structure with its hydrophobia city value. The output sequences Ob is created by replacing the structural elements [19,21] in Bs with the values, 200, 600, 800 for helix C, strand and coil respectively
• Solve the system identification problem, by performing NLCA de convolution with the output sequences Ob and the input sequence Ib to obtain the NLCA response, or the sought after running the algorithm.
• Transform the amino acid sequence of Tp into a discrete time sequences It, and convolve with F; thereby producing the predicted structure (Ot = It*F) of the target NLCA protein Fig 3, table 1,2.
• The result of this calculation Ot is a vector of numerical values. For values between 0 and 200, a helix C is predicted, and between 600 and 800, a strand is predicted by CA. All other values will be predicted as a coil by HACA. This produces mapping for the required target structure Ts of the target CA protein T
In the experiments conducted, the base proteins are assigned the values 300,700,900 for helix C, strand and coil respectively. We have found an structure numbering scheme that is build on Boolean characters of CA which predicts the coils, stands and helices separately .The HACA based prediction procedure [22-24] as described in the previous section is then executed, and each occurrence of each sequences in the resulting output, is predicted . The query sequence analyzer was designed and identification of the green terminals of the protein is simulated. The analysis of the sequence and the place of joining of the proteins are also pointed out.
Figure 2: Prediction Accuracy of protein coding reigns and promoter regions
Figure 3: Amino Acid Input
Table 1: Prediction Accuracy of protein coding reigns and promoter regions
Table 2: Prediction Accuracy for protein structure prediction
We have proposed a cellular automata classifier which can address major issues in bioinformatics. Extensive experiments are conducted for reporting the accuracy of the proposed tool. The average accuracy of HACA when tested with ENCODE, BG570, HMR195, Fickett and Tongue, ASP67 datasets is 78%. This work can be extended to achieve good classification accuracy for other problems in bioinformatics like genome annotation, sequence analysis etc.