ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
A. Anilet Bala1, Chiranjeeb Hati2 and CH Punith2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
A new image denoising method based on curvelet transform is proposed. The limitations of commonly used separable extensions of one-dimensional transforms, such as the Fourier and wavelet transforms, in capturing the geometry of image edges are well known. Here, we pursue "true" two-dimensional transform that can capture the intrinsic geometrical structure that is key in visual information. Denoising of an image is done by processing an image through Wiener filter and using curvelet transform [1], [6]. Experimental results show that proposed denoising technique performs better in terms of the PSNR. We have compared PSNR values of proposed algorithm with that of wavelet and curvelet in RBG and YCbCr regions.
Keywords |
| curvelets, discrete wavelet transform, FFT, radon transform, ridgelets, Wiener filter. |
INTRODUCTION |
| Visual perception has become an essential part of communication in today’s world. Because of which it is important to ensure that transmitted data is not corrupted by any kind of unwanted signals called noise. Noises are generated due to the improper modelling of production and/or capturing system of the signal. Therefore, real world signals usually contain deviations from the ideal signal that is expected. Image denoising is an important pre-processing task for further image processing such as edge detection or image segmentation. The main aim of any denoising algorithm is to reduce noise levels, while preserving the image features. At present day, there are various image denoising algorithms available which are successful in denoising a noisy image, but are inefficient in attaining better signal to noise ratio and/or retaining the image features. |
RELATED WORKS |
| Although the DWTs have established an impressive reputation as a tool for mathematical analysis and signal processing, it has the disadvantage of poor directionality, which has undermined its usage in many applications. Significant progress in the development of directional wavelets has been made in recent years. The complex wavelet transform have improved directional selectivity. However, the complex wavelet transform has not been widely used in the past, as it is difficult to design complex wavelets with perfect reconstruction properties and good filter characteristics. The dual-tree complex wavelet transform (DT CWT) proposed by Kingsbury [4], which added perfect reconstruction to the other attractive properties of complex wavelets. |
| The 2-D complex wavelets are essentially constructed by using tensor-product one-dimensional (1-D) wavelets. The directional selectivity provided by complex wavelets (six directions) is much better than that obtained by the classical DWTs (three directions), but is still limited. |
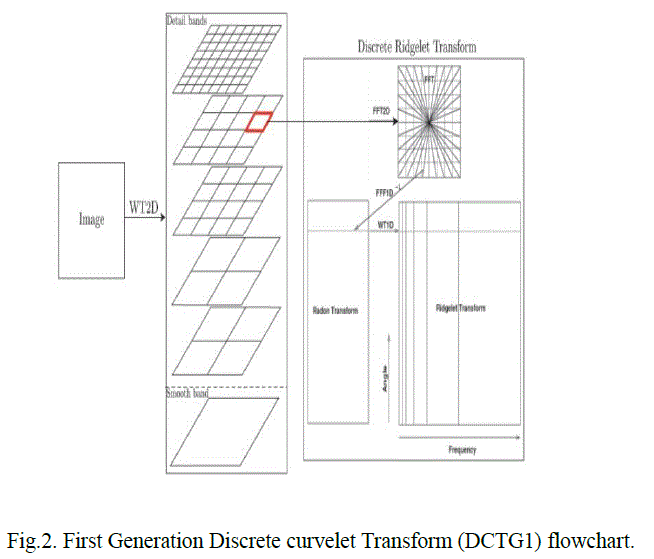
| In 1999, an anisotropic geometric wavelet transform, named ridgelet transform, was proposed by Candès and Donoho [6]. The ridgelet transform is optimal at representing straight-line singularities. Unfortunately, global straight-line singularities are rarely observed in real applications. To analyse local line or curve singularities, a natural idea is to consider a partition of the image, and then to apply the ridgelet transform to the obtained sub images. This block ridgeletbased transform, which is named curvelet transform, was first proposed by Candès and Donoho in 2000. |
PROPOSED ALGORITHM |
| In this paper, we propose a novel denoising method. The method uses curvelet transform and Wiener filtering [8] to denoise an image. Initially we obtain a noisy image by degrading it by adding additive Gaussian noise (most common type of noise). Then we implement our algorithm, which firstly passes it through a Wiener filter. And then the output of which is then applied by curvelet transform. The resultant image is denoised and also retains the important image information. Fig.1 shows the flow of the proposed algorithm. |
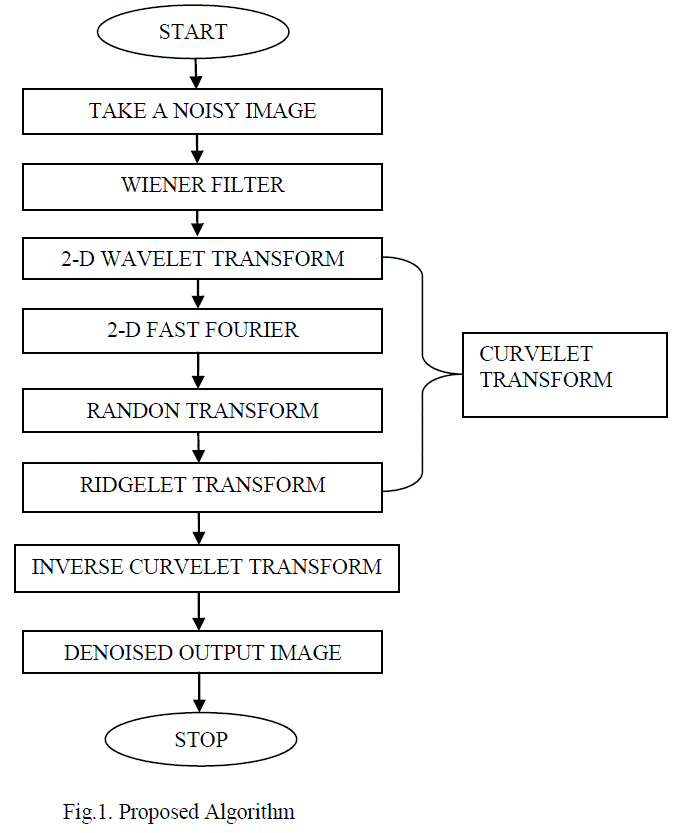 |
| A. WIENER FILTERING |
| The Wiener filter is commonly utilized because of its simplicity and its speed. It is deemed simple because it uses a system of linear equations to calculate a set of optimal filter weights that reduce the noise level of a received signal. It estimates cross-correlation and covariance matrices of noisy signals to calculate these weights and provide an accurate Estimate of the undistorted deterministic signal under Gaussian noise. The noise statistics are estimated and then used to determine a set of optimal filter weights. By then processing a new input signal, containing similar noise characteristics, with the optimal filter weights, the signal deterministic component is estimated. This method is optimal when the noise distribution is Gaussian. Furthermore, its execution only requires a few computational steps that are very fast to process. |
| The inverse filtering is a restoration technique for deconvolution, i.e., when the image is blurred by a known lowpass filter, it is possible to recover the image by inverse filtering or generalized inverse filtering. However, inverse filtering is very sensitive to additive noise. The approach of reducing one degradation at a time allows us to develop a restoration algorithm for each type of degradation and simply combine them. |
| The Wiener filtering executes an optimal trade-off between inverse filtering and noise smoothing. It removes the additive noise and inverts the blurring simultaneously. The Wiener filtering is optimal in terms of the mean square error. In other words, it minimizes the overall mean square error in the process of inverse filtering and noise smoothing. The Wiener filtering is a linear estimation of the original image. The approach is based on a stochastic framework. The orthogonality principle implies that the Wiener filter in Fourier domain can be expressed as follows: |
 |
 |
 |
 |
PERFORMANCE CALCULATION |
| In this paper, we presented a strategy for denoising a noisy image by the wiener and the curvelet transforms. The noise level in an image can be estimated by calculating the PSNR value. Therefore, performance can be measured by comparing the PSNR values of the noisy, curvelet and the proposed algorithm. Mean Square Error is defined as: |
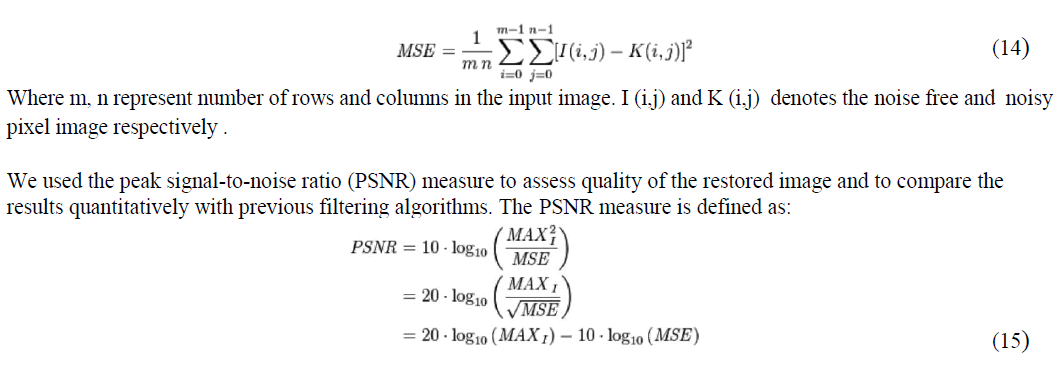 |
RESULT AND DISCUSSION |
| We test our algorithm with Peppers and Lena image. The tested images are corrupted with Gaussian white noise with noise standard deviation (σ) 10,20,30,40,50,60,70 respectively. The qualitative analysis of Peppers and Lena images, corrupted with White Gaussian noise, is shown in Fig. 3 and Fig. 5. The Peppers image corrupted with severe white Gaussian noise attack is demonstrated in Fig.3. Compare to curvelet algorithms, our proposed scheme highlights the best visible quality of the restored Peppers image. Table1 and 2 shows the simulation results, in terms of PSNR measure, for peppers and Lena standard images. In Table 1, our proposed scheme provided the best PSNR value for the Peppers image at various noise standard deviations. However, curvelet transform has given considerably low value. Fig. 4 and 6 shows the plot of PSNR values of proposed algorithm along with curvelet transform output and noisy image. We observed that the PSNR value of our proposed method is higher compare to curvelet transform and it works well for all the level of noises. |
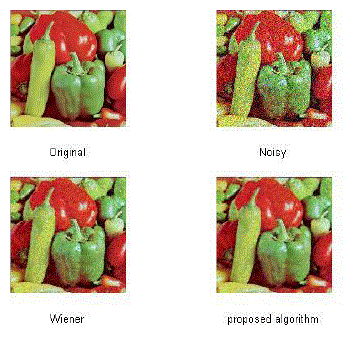 |
| Fig.3. Peppers image with σ = 40 dB (a) original input image i.e. without noise, (b) image contaminated with white Gaussian noise, (c) Output image of Wiener filter, (d) output image of the proposed method. |
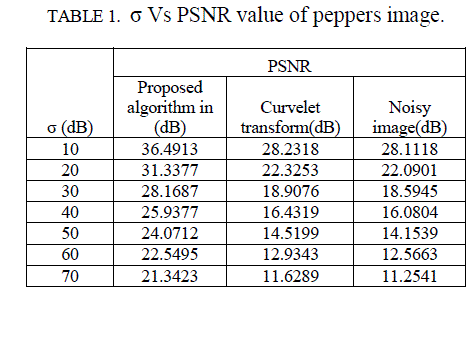 |
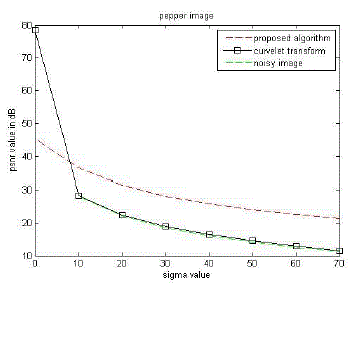 |
| Fig.4. Plots the PSNR values of proposed algorithm along with curvelet transform output and noisy image. |
 |
| Fig.5. Lena image with σ = 40dB (a) original input image i.e. without noise, (b) image contaminated with white Gaussian noise, (c) Output image of Wiener filter, (d) output image of the proposed method |
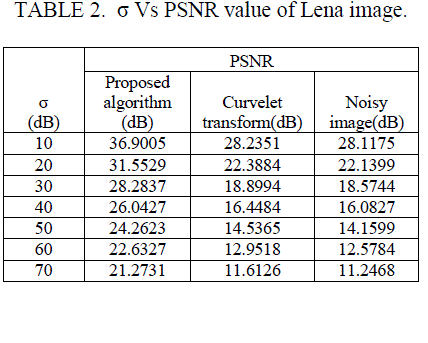 |
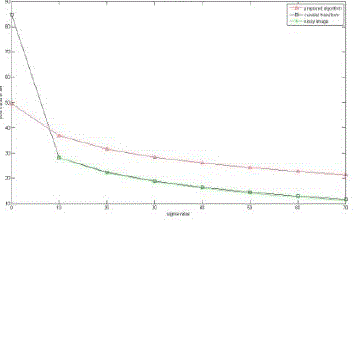 |
| Fig.6. Plots the PSNR values of proposed algorithm along with curvelet transform output and noisy image. |
CONCLUSION |
| Our proposed denoising algorithm has denoised pepper image and the PSNR value have been found to better than the curvelet and the wavelet transform. The algorithm performs even better in YCbCr region than in RGB region. The PSNR versus sigma graph has also been plotted which clearly explains that the proposed algorithm is more efficient. The graph shows a decrease in PSNR value as the sigma value increases, which is natural because, as the noise increases the signal to noise ratio is expected to decrease. |
References |
|