Implementation of a Bi-Variate Gaussian Random Number Generator on FPGA without Using Multipliers

Abstract

The multivariate Gaussian distribution is used to model random processes with distinct pair-wise correlations, such as stock prices that tend to rise and fall together. Multivariate Gaussian vectors with length n are usually produced by first generating a vector of n independent Gaussian samples, then multiplying with a correlation inducing matrix requiring Operations(n2) multiplications. This paper presents a method of generating bivariate vectors directly from the uniform distribution and eliminating the need for any multipliers. The method relies only on small read only memories and adders, and so can be implemented using only logic resources (lookup-tables and registers), saving multipliers, and block-memory resources for the numerical simulation that the multivariate generator is driving. As an optimization, only positive values are considered for the implementation. FPGA-optimized Random Number Generators (RNGs) used for uniform distribution are more resource efficient than software-optimized RNGs, as they can take advantage of bit-wise operations and FPGA-specific features. This paper use a new type of FPGA RNG called a LUT-SR RNG, which takes advantage of bit-wise XOR operations and the ability to turn LUTs into shift-registers of varying lengths. This paper model a Gaussian random number generator where its inputs elements are correlation matrix of standard deviation from previous history.

Keywords

Field-programmable gate array (FPGA), Monte Carlo simulation, bivariate samples, random number generation.

INTRODUCTION

THE multivariate Gaussian distribution is used to capture simple correlations between related stochastic processes, such as the stock prices of companies in similar business sectors, where the stock prices of companies in the sector tend to rise and fall together. To simulate the behavior of such processes, multivariate Gaussian random number generators (MVGRNGs) are used to generate random samples, which are then used to drive Monte Carlo simulations. Such simulations often require a huge number of independent runs in order to provide an accurate answer, such as the valueat- risk calculations performed by financial institutions, which are used to estimate how much money the institution might lose over the next day. Such long-running simulations are an ideal target for field programmable gate array (FPGA) acceleration, as they offer abundant parallelism, and are computationally bound [1]–[3]; however, they are reliant on a fast, resource-efficient, and accurate source of random samples from the multivariate Gaussian distribution. This paper is an implementation of a bivariate random number generator was resource usage to standard bit-wise logic elements.

This paper follows

1) An algorithm for generating samples from the multivariate Gaussian distribution using only uniform random bits, table- lookup, and addition;

2)A hardware architecture for implementing an MVGRNG using only lookup-tables (LUTs) and flip-flops (FFs), which allows a regular densely-packed placement strategy and achieves 500 MHz+ clock speeds.

MULTIVARIATE GAUSSIAN RANDOM NUMBERS

Generation of the univariate Gaussian distribution with a specific mean, μ, and variance, σ2, is achieved by first generating a standard Gaussian variate ‘r’ with mean zero and variance one, then applying a linear transformation

An alternative method is to use the singular value decomposition (SVD) algorithm. This decomposes the matrix into an orthogonal matrix U and a diagonal matrix S, such that Σ = USUT . This decomposition allows the construction of the solution A = U √ S. The disadvantage of the SVD-based construction is that in general all the elements of the matrix are nonzero, resulting in an n2 cost in both the number of stored elements, and in the number of multiply-accumulates per transformed vector. However, the SVD algorithm is able to handle a wider range of covariance matrices, such as illconditioned matrices that are very close to singular and reduced rank matrices, where the output vector depends on fewer than n random factors. Such difficult covariance matrices frequently occur in practice [7], so this paper focuses on the use of a dense SVD-style decomposition.

GENERATION USING LUTS AND ADDERS

The standard generation method uses direct matrix multiplication, forming each output element from a linear combination of r (the vector of n IID Gaussian samples)

HARDWARE ARCHITECTURE

The central idea in this paper, of replacing Gaussian samples and multipliers with uniform samples and tables, allows for many types of possible implementations. For example, the tables can be implemented using LUTs or block-RAMs, and the generator can vary in throughput from 1 to n cycles per generated vector. This paper focuses on the highest performance mode of the generator, to provide the maximum contrast with previous implementations, while still providing good efficiency and quality. The specific choices made are as follows.

1) Logic Resources Only: tables are implemented using LUTs, so the only resources used are LUTs and FFs (no DSPs or block-RAMs).

2) Parallel Generation: the generator operates in a fully parallel mode, providing one new n-element vector per cycle, unlike previous approaches which generated one vector for every n cycle.

3) Maximum Clock Rate: the generator operates at the maximum realistic clock-rate for the target FPGA. For the Virtex-5 this is effectively 550 MHz, as this is the maximum clock rate of the DSP and RAM blocks that will be used in the simulation that the generator is driving.

4) Regular Architecture: simulations typically consume almost all resources in the FPGA (due to replication of simulation cores), and a regular, explicitly placed highly routable, and generator allows fast place-and route while still achieving high overall clock-rate.

5) No Matrix Specialization: the generator is not optimized for a specific correlation matrix, and should support the loading of any correlation structure without structural modification.

SIMULATIONS AND EXPERIMENTAL RESULTS

For the simulation purpose the σ values of the covariance matrices, clock and a reset signal are given as inputs. The σ values can be obtained from the expert advice or from the previous experience. The clock can attain the maximum value of the used platform. The reset is made logic high for one clock for loading the sigma values i.e. the covariance matrices values and then the random number generated for corresponding σ values is available in every clock cycle after reset is made logic low. Output is random numbers for the corresponding experiment for which it can be used for fast simulations like Monte Carlo simulation.

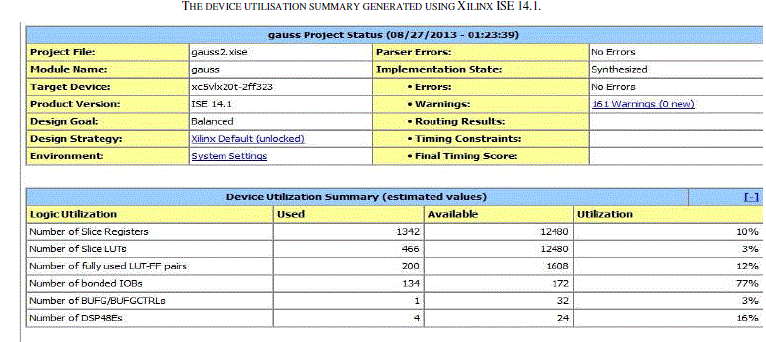
For memory optimization and bit representation and evaluation in Xilinx, we in this experiment use σ values represented as bits. The bits can vary from 0.0000 to 9.9999, 105 values can be represented by this method by using 217 bits. This reduces the memory utilization to a great extent.So the real value of σ values is converted into its corresponding bits representation which can be obtained by multiplying the value with 104 converting it into binary and appending zeros to the MSB. So by this method real value 1 is equivalent to binary of 1000 and real value of 2 is equivalent to binary of 2000. So the 1, 2 and 3 can be represented respectively as 00010011100010000, 00100111000100000, and 00111010100110000.

The output random number generated is also in the binary format of 32 bits because of the addition involved in obtaining output and it can be converted into its real values by multiplying with 10-8 and convert to decimal. The obtained σ values are used for updating the LUT values by multiplying each RAM values with the corresponding covariance matrics values (σ values). Then this updated RAM-LUT is used for random number generation.

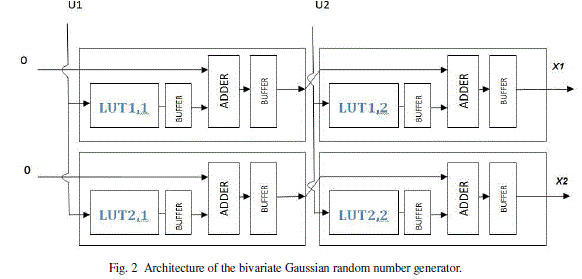A bivariate random number generator is implemented in the vertex 5 platform and many optimizations are done for the fast processing and less memory usage. An optimization is on avoiding the negative values understanding that the Gaussian profile maps its mirror image in both positive and negative side. So the adder used here works in the first quadrant. The LUTs used here also avoids negative values and reduce memory in terms of an extra bit needed to indicate it. This also gives more accurate outputs as the number of samples taken exactly doubles. The values stored in the LUT’S have equal probability [5].

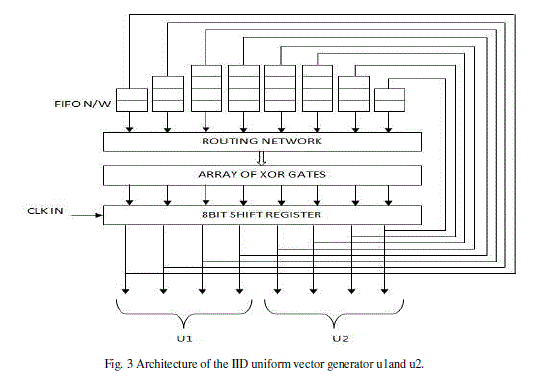This type of FPGA-optimized uniform random number generator, called a LUT-SR RNG. These RNGs takes advantage of the ability to configure LUTs as independent shift-registers, allowing high-quality long period generators to be implemented using only a small amount of logic. In addition the period and quality scale with the number of output bits, unlike generators adapted from software. A key advantage of the LUT-SR generators over previous FPGAoptimized uniform random number generators is that they can be reconstructed using a simple algorithms. In concert with the tables of maximum period generators, this allows FPGA engineers to use the new RNGs without needing to find generator instances themselves [6].

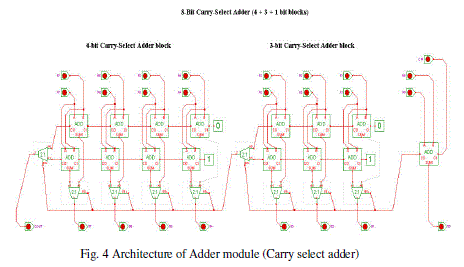Carry select adder is used for the fast addition. The basic idea is to add 2 bits using 3 1-bit full adders and a 2-bit multiplexer. One adder adds the least significant bit in the normal fashion. The other two add the most significant bit, one of them assuming that the carry in will be 0 and the other assuming that the carry in will be 1. Then the multiplexer chooses the output from one of these adders based on the carry produced by the adder for the least significant bit [8].

TABLE II

THE TIMING ANALYSIS REPORT.

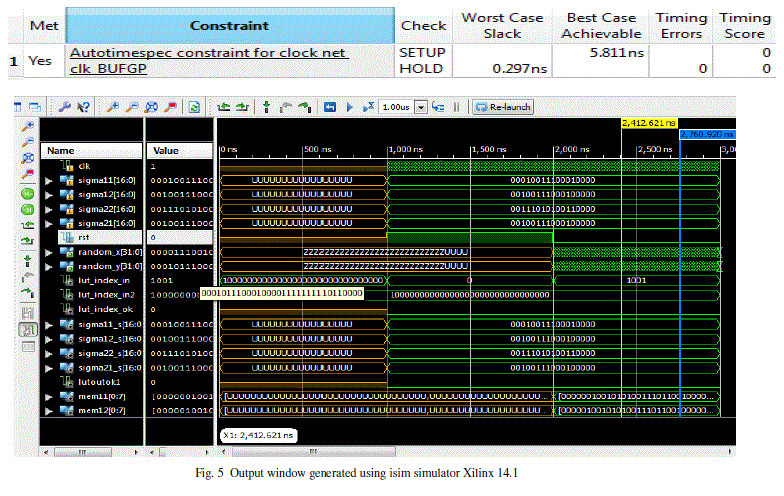CONCLUSION

This paper presented a method for bi-variate Gaussian random number generator in FPGAs, which decomposes the generation into a series of table-lookups and additions. This method can be extended to use in numerical Monte Carlo simulations; risk analysis etc as it only uses LUTs and FFs, and so all DSP and block-RAM resources can be used in the simulation core that the generator is driving. This can be extended to multivariate generators as a future work. Adder/subtracter module can be included for getting more accurate and extended values.

ACKNOWLEDGMENT

The authors would like to thank the Department of Electronics and communication, SNGCE Kadayirippu for their support. We would also like to thank friends and resource persons who give technical support, valuable advice and encouragement throughout the project.

References

D. B. Thomas and W. Luk, “Credit risk modelling using hardware accelerated monte-carlo simulation,” in Proc. ACM Symp. FPGAs Custom Comput. ach., 2008, pp. 229–238. N. Woods and T. VanCourt, “FPGA acceleration of Quasi-Monte Carlo in finance,” in Proc. Int. Conf. Field Programm. Logic Appl., 2008, pp. 335–340. A. Kaganov, P. Chow, and A. Lakhany, “FPGA acceleration of Monte- Carlo based credit derivative pricing,” in Proc. Int. Conf. Field Programm. Logic Appl., 2008, pp. 329–334. D. B. Thomas and W. Luk, “Multivariate Gaussian random number generation targeting reconfigurable hardware,” ACM Trans. Recon. Technol. Syst., vol. no. 12, pp. 22–26, 2008. Multiplierless Algorithm for Multivariate Gaussian Random Number Generation in FPGAs David B. Thomas, Member, IEEE, and Wayne Luk, Fellow, IEEE FPGA-Optimised Uniform Random Number Generators using LUTs and Shift Registers David B. Thomas and Wayne Luk Imperial College London Bedrij, O. J., (1962), “Carry-select adder,” IRE Trans. Electron. Comput. Pp.340–344.