Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Implementation of FFT Based Automatic Image Mosaicing

Vinod.G.R 1, Mrs. Anita R 2
  1. PG Student [VLSI & Embedded systems], Dept. of ECE, EPCET, Bangalore, Karnataka, India
  2. Associate professor, Dept. of ECE, EPCET, Bangalore, Karnataka, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper proposes FPGA implementation technique to generate a panoramic view by combining images. Image mosaicing is useful for a variety of tasks in vision and computer graphics. It presents a complete system for stitching a sequence of images with some amount of overlapping between every two successive images. There are three contributions in this paper. First is an image registration method which handles rotation and translation between the two images using FFT phase correlation. Second is an efficient method of stitching of registered images using the registration parameters obtained in previous step using pixel mapping method. Third is image blending where the seam present in the stitched image is removed by weighted average blending method.

Keywords
FFT Phase Correlation, Registration, Rotation, Translation, Image Stitching, Image Blending.

INTRODUCTION
An Image mosaic is a composition generated from a sequence of still images. By applying methods shown in this paper parameters which are used to get the mosaic of images can be obtained, it is possible to construct a single image from many images with some overlapping areas, covering the entire visible area of the scene. The steps in mosaicing are image registration, image stitching and image blending.
Image registration refers to the geometric alignment of a set of images. The set may consist of two or more digital images taken of a single scene from different sensors, or from different viewpoints. The goal of registration is to establish geometric correspondence between the images so that they may be transformed, compared, and analyzed in a common reference frame. This is of practical importance in many fields, including remote sensing, medical imaging, and computer vision.
The registration method presented here uses the Fourier domain approach to match images that are translated and rotated with respect to one another. Fourier methods differfrom other registration strategies because they search for the optimal match according to information in the frequency domain. The algorithm uses the property of phase correlation for automatic registration, which gives the translation parameters between two images by showing a distinct peak at the point of the displacement. With this as the basis, rotation is also found.
The next step, following registration, is image stitching. Image integration or image stitching is a process of overlaying images together on a bigger canvas. The images are placed appropriately on the bigger canvas using registration parameters to get the final mosaic by pixel mapping method. At this stage, the main concerns are in respect of the quality of the mosaic and the efficiency of the algorithm used. In this paper, an efficient method for stitching multiple images has been proposed.
Next step is image blending, where due to the light variation in the two images which are stitched a seam appears. To get seamless image weighted average blending method is used.

BLOCK DIAGRAM
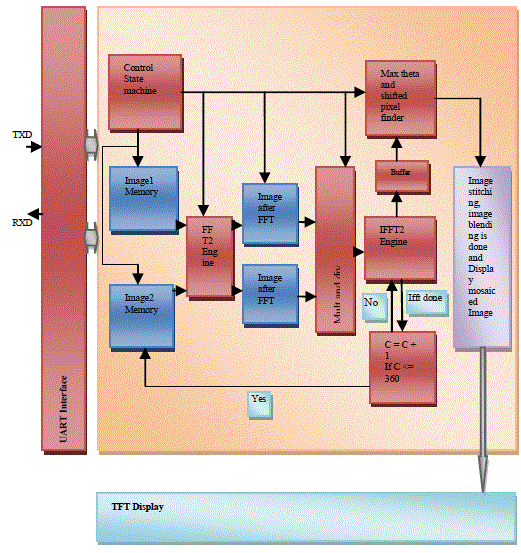
Figure 1 shows the block diagram of the implementation of image mosaicing. At first hex file is generated from the input images and from UART that file is sent to FPGA memory where image registration, image stitching and image blending is done to get final mosaiced image.
Steps used for implementing FFT based automatic image mosaicing is shown below.
1. Image is converted to hex file and that file is sent to memory through UART.
2. Images stored in memory are sent to FFT engine where FFT is calculated and those are sent to multiplier and divider block.
3. After that IFFT is calculated and then phase correlation is calculated. Through this registration values are obtained.
4. Registration parameters are used for image stitching by pixel mapping method.
5. Image blending is done to remove seam using weighted average blending method.
6. Finally mosaiced image is displayed on TFT display.

IMAGE REGISTRATION

ESTIMATION OF ROTATION PARAMETERS:
Suppose the two images I1 and I2 to be registered involve both translation and rotation with angle of rotation being “θ” between them. When I2 is rotated by θ, there will be only translation left between the images and the phase correlation with I1 should give maximum peak. So by rotating I2 by one degree each time and computing the correlation peak for that angle, we reach a stage where there is only translation left between the images, which are characterized by the highest peak for the phase correlation. That angle becomes the angle of rotation“θ”.

TRANSLATION PARAMETER ESTIMATION:
If f (x, y) ⇔F(ξ,η) then
f(x,y)exp[j2π(ξx0+ηy0)/ N] )⇔ F(ξ- ξ0,η- η0) and f(x-x0,y-y0)⇔ F(ξ,η).exp[-j2π(ξx0+ηy0)/ N]
where the double arrow (⇔ ) indicates the correspondence between f (x, y) and its Fourier transform F. According to this property, also called as Fourier Shift Theorem, if a certain function’s origin is translated by certain units, then the translation appears in the phase of the Fourier transform. i.e. if f and f‟ are two images that differ only by a displacement (x0, y0) i.e., f′(x,y)=f(x-x0,y-y0)
Then, their corresponding Fourier transforms F1 and F2 are related by
F'(ξ,η) = e-j2π(ξx0+ηy0)*F(ξ,η).
The cross-power spectrum of two images f and f” with Fourier transforms F and F” is defined as
F(ξ,η).F'*( ξ,η)/│F(ξ,η).F'*( ξ,η)│=ej2π(ξx0+ηy0)
where F”* is the complex conjugate of F”, the shift theorem guarantees that the phase of the cross-power spectrum is equivalent to the phase difference between the images. By taking inverse Fourier transform of the representation in the frequency domain, we will have a function that is an impulse, that is, it is approximately zero everywhere except at the displacement that is needed to optimally register the two images. If there is no other transformation between f1 and f2 other than translation, then there is distinct peak at the point of the displacement.
The discussion in the above section tells that whenever there is pure translation present between two images, phase correlation has a maximum peak and the corresponding location gives the translation parameters (x0, y0).

PROPOSED ALGORITHM:
Now, we present the Algorithm for estimation of rotation and translation parameters which were discussed in the previous two sections. (We can down sample images to speed up the process of registration)
Algorithm1:
Input: Two overlapping images I1 and I2
Output:
Registration parameters (tx, ty, θ) wheretx and ty are translation in x and y directions respectively and θ is the rotation parameter.
Steps:
1. Read and resize the two images. Let the resized images be I1' and I2'.
2. For i = 1: step: 360
2.1) Rotate I2' by i degrees. Let the rotated image be I2'rot.
2.1) Rotate I2' by i degrees. Let the rotated image be I2'rot.
2.3) Let Q(u,v) be the Phase correlation value of I1' and I2'rot, based on FI1' and FI2'rot.
Q(u,v)=FI1”(u,v).FI2'rot*(u,v) │FI1”(u,v)F'I2”rot*(u,v)│
2.4) Compute the inverse Fourier transform q(x, y) of Q (u, v).
2.5) Locate the peak of q(x,y).
2.6) Store the peak value in a vector at position i. End For.
3. Find the index of maximum peak from the values stored in the vector in step 2.6. It gives the angle of rotation. Let it be θ'.
4. Repeat steps 2.1 to 2.6 for i = θ'-step :θ'+step.
5. Find the angle of maximum peak from step 4. It becomes the angle of rotation. Let it be θ.
6. Rotate the original image I2 by “θ”. Let the rotated image be I2rot.
7. Phase correlate I1 and I2rot. Let the result be P(u,v).
8. Compute the inverse Fourier transform p(x,y) of P(u,v).
9. Locate the position (tx, ty) of the peak of p(x, y) which become the translation parameters.
10. Output the parameters (tx, ty, θ).
The above algorithm is capable of finding rotation between the images. The maximum peak occurs only at the point where there exists pure translation between the images.
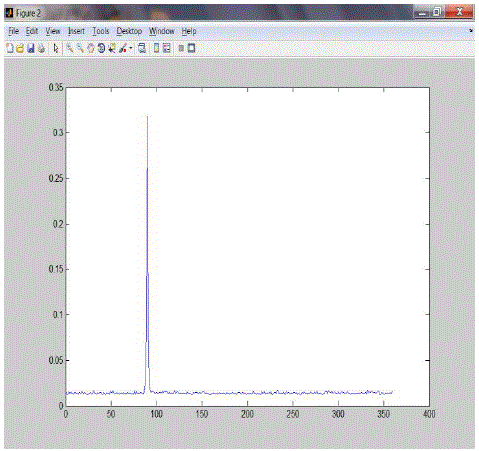
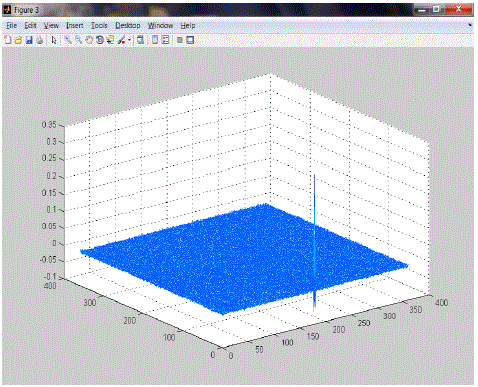
As an example, for an input pair of images fig 2 and fig 3 with a translation of 31 pixels along the column (x) direction and along row (y) direction 201 pixels and also with rotation of 90 degrees. The plot of the phase correlation between the images is shown in fig 3 and fig 4.
In figure 4 we can see peak at the 90 degree point showing that the 2nd input image is rotated by 90 degree with respect to 1st input image.
Figure 5 shows the peak at the points where there is exact translation is present between two images along X and Y directions(X=31 and Y=201).

IMAGE STITCHING
Image stitching is the next step following the registration. At this stage, the reference image is overlaid on the source image by pasting its pixels on a canvas at the appropriate location using the transformation parameters obtained in the registration process. In this section, we present a general algorithm for stitching any number of images.

PROPOSED ALGORITHM:
Algorithm2:
1. Create a canvas: The canvas is for the mosaic of all the images. We call it image canvas.
2. Make the entire canvas black.
3. For a given image I, For each pixel in the image I, Paste a mapped pixel on the canvas, taking in to consideration the translational and rotational parameters.
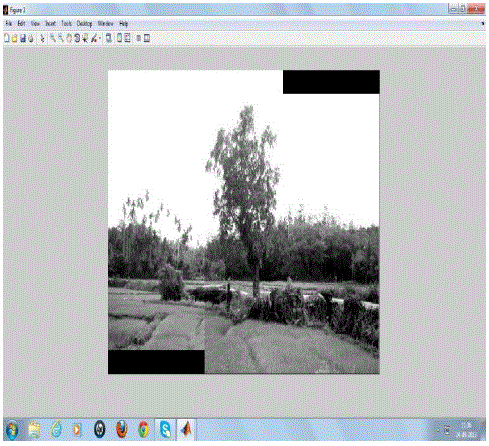
Fig 6 shows mosaic image of two input images with seam.

ADVANTAGES OF THE ABOVE METHOD:
This algorithm is very efficient in stitching multiple images with large overlaps. Consider a sequence of image with, let us say, 80% overlap between the successive images. If the entire image is pasted every time, then some of the pixels in the overlap region get mapped four times , thus leading to a 300% redundancy in pasting where as algorithm 2 pastes each pixel only once. This approach not only improves the efficiency of the stitching but the same time retains the quality of the mosaic closer to that of the input images.

IMAGE BLENDING
Image blending is the last step. The two images which are given has inputs, if these images are taken at different lighting conditions, a seam will appear in the stitched image where two images can be easily distinguishable. So to improve quality of image seam should be removed. Hence weighted average blending method is used to remove the seam. General algorithm for blending is shown below.
PROPOSED ALGORITHM:
Algorithm 3:
1. Find the orientation of growth of the canvas on which the mosaic has to be created.
2. Obtain the minimum rectangle containing the entire region of overlap between the images.
3. Obtain a small region of length “l” and breadth “b” along the seam using the information in step 2 which depends on the region of overlap and direction of growth of the canvas.
4. Blend the region using Weighted Average Blending.
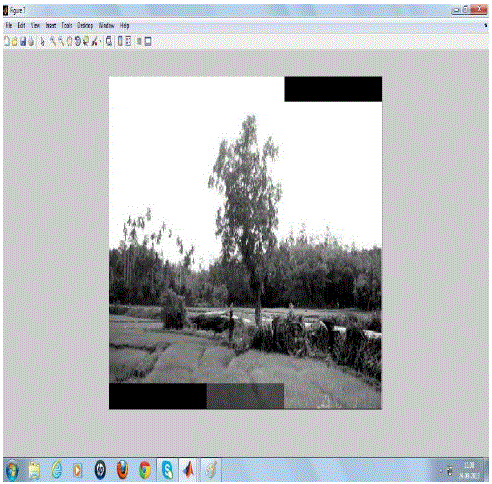
Figure 7 shows the final mosaiced image without any seam.

EXPERIMENTAL RESULTS
The algorithm 1 for registration, algorithm 2 for stitching and algorithm 3 for blending as described in 3, 4 and 5 sections respectively have been realized in Verilog HDL and implemented using XC6SLX16-CSG324C Xilinx Spartan-6 Nexys 3 FPGA device.These algorithms have been tested on different sets of images, especially real images involving large amounts of rotational and translational changes for registration and illumination and view changes for image composition.

CONCLUSIONS
Three algorithms for still image sequences are presented here. The first is a simple and reliable algorithm for finding rotation and transformations of planar transformations based on the FFT phase correlation. The overall complexity is dominated by FFT. A key feature of Fourier-based registration methods is the speed offered by the use of FFT routines. The next is a method of stitching images which overcomes redundancy in re-pasting pixels in the final mosaic and this is done by pixel mapping method. Last one is image blending, it is done using weighted average blending method and this method is very efficient in removing seam in image by retaining the quality of image. All the algorithms are successfully implemented on the Spartan6 FPGA, with efficient hardware utilization and the results are found to be accurate

Figures at a glance
Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4
Figure Figure Figure
Figure 5 Figure 6 Figure 7

References