Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Implementation of High Speed Signed Multiplier Using Compressor

D.Srinu1, S.Rambabu2, G.Leenendra Chowdary3
  1. M.Tech, Dept of ECE, SITE, Tadepalligudem, A.P, India
  2. Asst. Professor, Dept of ECE, SITE, Tadepalligudem, A.P, India
  3. Asst. Professor, Dept of ECE, SITE, Tadepalligudem, A.P, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Multipliers play an important role in today’s digital signal processing and various other applications. With advances in technology, many researchers have tried and are trying to design multipliers which offer either of the following design targets – high speed, low power consumption, regularity of layout and hence less area for compact VLSI implementation. This work is based on one of the ancient Vedic algorithms (sutras) called Urdhava tiryakbhyam method. These sutras are meant for faster calculation. Though faster when implemented in hardware, it consumes less area. This paper presents a technique to modify the architecture of the Urdhava Tiryakbhyam hardware by using 3_2compressor in order to reduce area and delay to improve overall performance. The coding is done for 16 bit (Q15format), 32 bit (Q31format) and 64 bit (Q63 format) fixed point Q-format by using Verilog HDL and Synthesized by using Xilinx ISE version 9.2i. The performance is compared in terms of area, delay with earlier existing architecture of Urdhava Tiryakbhyam method. The proposed work (compressor based Urdhava Tiryakbhyam method) shows improvements in terms of area and time delay.



 

Keywords
Compressor, Fixed point format, Q-format, Urdhava Tiryakbhyam.

INTRODUCTION
Vedic Mathematics is the ancient system of mathematics which was rediscovered early last century by Sri Bharati Krishna Tirthaji (1884-1960) [1] .The Sanskrit word “Veda” means “knowledge”. He organized and classified the whole of Vedic Mathematics into 16 formulae or also called as sutras. These formulae form the backbone of Vedic mathematics. Great amount of research has been done all these years to implement algorithms of Vedic mathematics on processors. Hence our focus in this work is to develop optimized hardware modules for multiplication operation. Considering fixed point representation, 16 bit Q15 format, 32 bit Q31 format and 64 bit Q63 formats are provide required precision for most of the digital signal processing applications and best suited for implementation on processors. In this paper we propose the implementation of fixed point Q-format [6] high speed multiplier using Urdhava Tiryakbhyam method of Vedic mathematics. Further we have also implemented multipliers using compressor based Urdhava Tiryakbhyam method.
The paper is organized into VI sections. Section II explains fixed point arithmetic III Urdhava Tiryakbhyam method of Vedic mathematics; IV explains the architecture of proposed compressor based Urdhava multipliers; V Presents the simulation results and Comparison of Q format multipliers and lastly VI provides conclusion of the work.

A. Literature Review:
The application which we are considering describes about the information about all the basic Vedic mathematics techniques [1] used for various operations. Among these techniques more preferable method is Urdhva tiryakbhyam method to describe Urdhava tiryakbhyam methodology [3] and their hardware architecture [4] details and implementation [5] presented. The algorithm to architecture mapping using floating point number representation Consumes more hardware which tends to be expensive.Fixed point number representation [6] is a good option to implement at silicon level. Hence our focus in this work is to develop optimized hardware modules for multiplication operation .To performing multiplication operations for various types of Q- formats [2] architectures (Q15, Q31, and Q63 formats) used. In this paper the proposed work is the implementation of compressor [7, 8] based tiryakbhyam methodology to reduce area and time delay to improve overall performance.

FIXED POINT ARITHMETIC
An N-bit fixed-point number [6] can be interpreted as either: an integer (i.e.20640), a fractional number (i.e.0.78). In a 16-bit processor dynamic range in between -32,768 to 32,767.
Example for integer fixed-point number: 200 × 300 = 60000, this is an overflow. This is difficult to use in processors due to possible overflow. To overcome overflow draw back fractional fixed-Point Representation will be used which is suitable for DSP algorithms. An N-bit fixed point 2’s complement representation as follows.
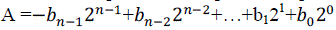image
Equation (1) shows fractional fixed point representation. Fractional number range is between 1 and -1. Multiplying a fraction by a fraction always results in a fraction and will not produce an overflow (e.g., 0.99 x 0.9999 less than 1) Successive additions may cause overflow .To represent fractional numbers in-between -1.0 and 1-2�������� where N is the number of bits.

A.Q- Format Representation:
In general any Q-format representation is denoted by Qm.n notation where m is the number of bits for integer portion ,n denotes number of bits for fractional portion Total number of bits N = m + n + 1, for signed numbers.
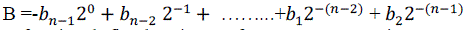image
Equation (2) shows fractional fixed point Q_format representation.Example for Q-format representation: 16-bit number(N=16) and Q2.13 format 2 bits for integer portion, 13 bits for fractional portion, 1 signed bit (MSB). Special cases: 16-bit integer number (N=16) => Q15.0 format 16-bit fractional number (N = 16) => Q0.15 format; also known as Q.15 or Q15.

B. Q-Format Multiplication:
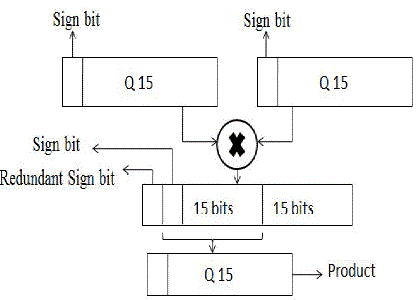
When two Q15 numbers are multiplied their product is 32 bits long as illustrated in Fig. 1. The product has a redundant or extended sign bit. Since the product stored in memory should also be a Q15 number we left shift the product by one bit and the most significant 16 bits (including sign bit) is stored in the memory. Product of two Q15 numbers is Q30.So we must remember that the 32-bit product has two bits in front of the binary point. Since NxN multiplication yields 2N-1 result Addition MSB sign extension bit typically only the most significant 15 bits (plus the sign bit) are stored back into memory, so the write operation requires a left shift by one. Fig.1. demonstrates multiplication of two Q15 format numbers. The process remains same for Q31format and Q63 format.
When we want to convert a fractional number in the range of the desired Qm.n format, we multiply it with 2n. The resultant value is truncated or rounded off to the nearest integer. Therefore a small amount of precision loss is involved which reduces as the number of bits representing the fractional part increases. We prefer rounding technique since its error bias in both positive and negative direction is same. Therefore the rounded value will be more precise. For e.g. Conversion of 0.2625 to Q15 format is done by multiplying it with 215 which equals to 8601.6 which when rounded gives 8602.This is stored as 0010000110011010 in a 16 bit memory location. The most significant bit indicates sign of the number. If it is negative then 2’s complement method is followed to store the number. Thus a fraction is converted to an integer in a Q-format and the choice of the decimal point lies entirely in the hands of the programmer.

URDHAVA TIRYAKBHYAM METHOD
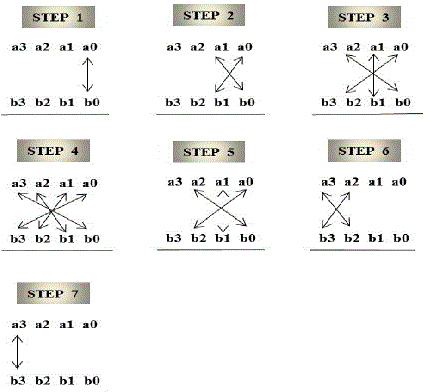
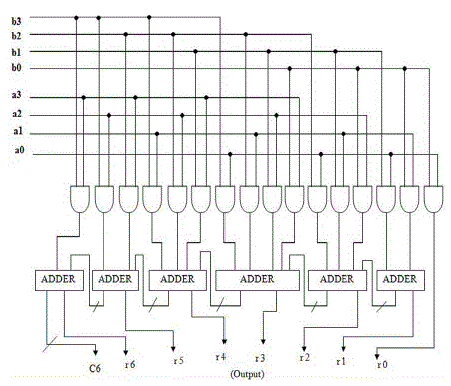
Urdhava Tiryakbhyam [3] is a Sanskrit word which means vertically and crosswire in English. The method is a general multiplication formula applicable to all cases of multiplication. It is based on a novel concept through which all partial products are generated concurrently.
Fig. 2, the least significant bit (LSB) of the multiplier is multiplied with least significant bit of the multiplicand (vertical multiplication). This result forms the LSB of the product. In step 2 next higher bit of the multiplier is multiplied with the LSB of the multiplicand and the LSB of the multiplier is multiplied with the next higher bit of the multiplicand (crosswire multiplication). These two partial products are added and the LSB of the sum is the next higher bit of the final product and the remaining bits are carried to the next step the Partial products and their sums for every step can be calculated in parallel. Thus every step in fig. 2 has a corresponding expression as Follows:
r0=a0b0. …………………………………..….step (1)
c1r1=a1b0+a0b1………………………….….…step (2)
c2r2=c1+a2b0+a1b1 + a0b2…………….….. ...step (3)
c3r3=c2+a3b0+a2b1 + a1b2 + a0b3………..… step (4)
c4r4=c3+a3b1+a2b2 + a1b3……………...…....step (5)
c5r5=c4+a3b2+a2b3………………………...…step (6)
c6r6=c5+a3b3…………………………….........step (7)
With c6r6r5r4r3r2r1r0 being the final product [5]. Hence this is the general mathematical formula applicable to all cases of multiplication and its hardware architecture is shown in fig.4.In order to multiply two 8-bit numbers using 4- bit multiplier we proceed as follows. When the numbers are multiplied according to Urdhava Tiryakbhyam (vertically and crosswire) method, we get
AH AL BH BL ------------ (AH x BH) + (AH x BL + BH x AL) + (AL x BL).
Thus we need four 4-bit multipliers and two adders to add the partial products and 4-bit intermediate carry generated. Since product of a 4 x 4 multiplier is 8 bits long, in every step the least significant 4 bits correspond to the product and the remaining 4 bits are carried to the next step. This process continues for 3 steps in this case. Similarly, 16 bit multiplier has four 8 x 8 multiplier and two 16 bit adders with 8 bit carry. Therefore we see that the multiplier is highly modular in nature. Hence it leads to regularity and scalability of the multiplier layout.

ARCHITECTURE
Q-format signed multiplier includes Urdhva tiryakbhyam integer multiplier [4] with certain modifications as follows.

A.3_2 Compressor:
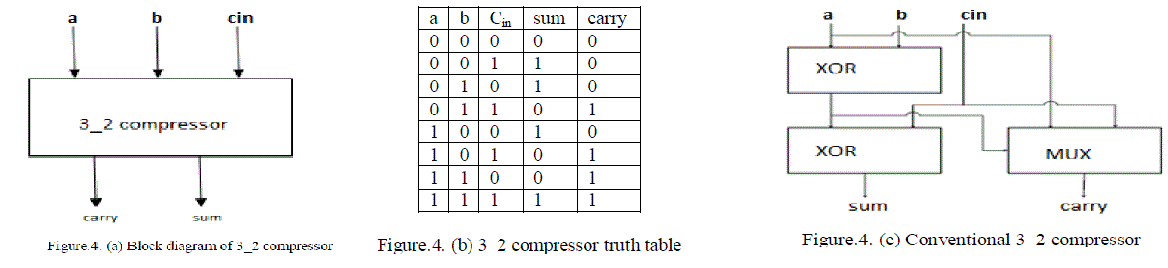
High speed multipliers use 3-2, 4-2 and 5-2 compressors to lower the latency of partial product reduction part [7, 8]. Compressors are used to minimize delay and area which leads to increase the performance of the overall system. Compressors are generally designed by XOR-XNOR gates and multiplexers. A compressor is a device which is used to reduce the operands while adding terms of partial products in multipliers. The most widely and the simplest used compressor is the 3-2 compressor which is also known as a full adder. A 3-2 compressor has three inputs X1, X2, X3 and generates two Outputs they are sum and the carry bits. The block diagram of 3-2 compressor is shown in figure.4. (a) And truth table for 3-2 compressor is shown in figure.4. (b).
Figure 4. (c) Has two XOR gates in the critical path. The sum output is generated by the second XOR and carry output is generated by the multiplexer (MUX). The equations (3, 4, and 5) governing the conventional 3-2 compressor outputs are shown below.
The conventional architectures of 3-2 compressor shown in figure 4. (c).
a +b +Cin=sum+2●carry………………….Equation (3)
Sum=a ⊕b⊕ Cin. …………………………………….Equation (4)
Carry= (a⊕ b) ● Cin+ (a⊕ b) ●a..............Equation (5)
Considering a 16 bit Q15 multiplier, the product is also a Q15 number which is 16 bits long.
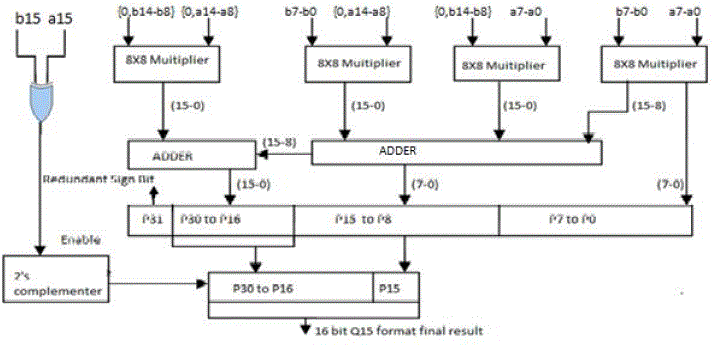
Firstly, if the MSB of input is 1 then it is a negative number. Therefore 2’s complement of the number is taken before proceeding with multiplication. Since the MSB denotes sign it is excluded and a ‘0’ is placed in this position while multiplying. A Q15 format multiplier consists of four 8 x 8 Urdhava multipliers and the resulting product is 32 bits Long as shown in fig. 5.
Therefore the 32 bit product is left shifted by 1 bit to remove the redundant sign bit and only the most significant 16 bits of this product are considered which constitute the final product. An xor operation is performed on the input sign bits to determine the sign of the result. If the output is ‘1’it enables the conversion of the 16 bit final result to its 2’s compliment format indicating a negative product.
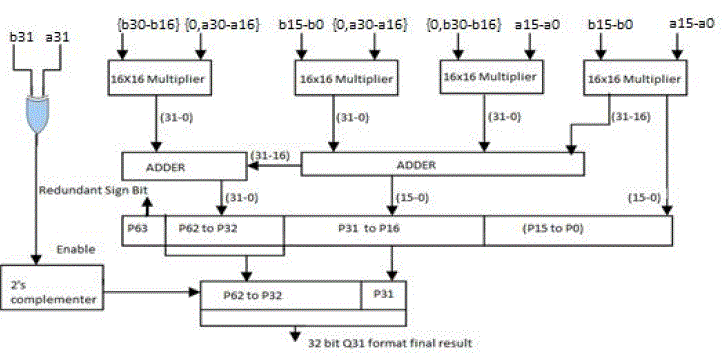
In fig. 6 but the product of a Q31 number is also a Q31number which should be 32 bits long. Therefore the 64 bit product is left shifted by 1 bit to remove the redundant sign bit and only the most significant 32 bits of this product are considered which constitute the final product. A xor operation is performed on the input sign bits to determine the sign of the result. If the output is ‘1’it enables the conversion of the 32 bit final result to its 2’s compliment format indicating a negative product.
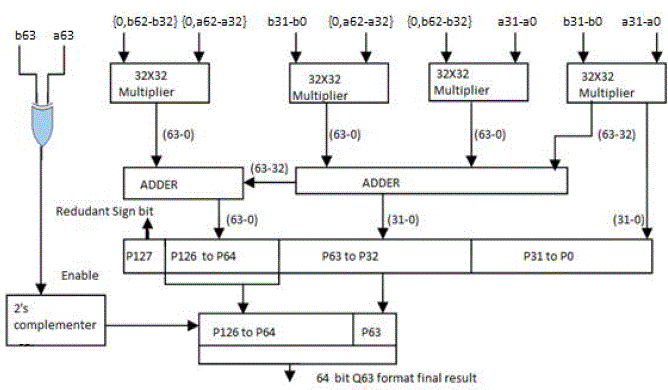
Similarly as shown in fig. 7 but the product of a Q63 number is also a Q63 number which should be 64 bits long. Therefore the 128 bit product is left shifted by 1 bit to remove the redundant sign bit and only the most significant 64 bits of this product are considered which constitute the final product. A xor operation is performed on the input sign bits to determine the sign of the result. If the output is ‘1’it enables the conversion of the 64 bit final result to its 2’s compliment format indicating a negative product.

SIMULATION RESULTS
The proposed compressor based Urdhava tirykbhyam Q_format multiplier is designed using verilog HDL and structural form of coding. The basic block of both Q15, Q31and Q63 multipliers is a 4 x 4 Urdhava Tiryakbhyam integer multiplier which in turn is made up of two 2 x 2 multiplier blocks.. The Code is completely synthesized using Xilinx XST and Implemented on device family Virtex-5, device XC5VL50, Package FF324 with speed grade -2.

A. Simulation Results For Q-format Multipliers:
The design was simulated using Isim on Xilinx ISE 9.2i version. For Q15 format multiplication as shown in fig. 5.
Input1 = -0.75 = 1010000000000000
Input2 = - 0.25 = 1100 000000000000
Output = 0.1875 = 0001100000000000
For Q31 format multiplication as shown in fig. 6.
Input1=0.333333= 00101010101010101010011111011111
Input2=-0.666666= 10101010101010101011000001000010
Output=-0.2222217777743935585021972655625= 11111000 1110 0011 0001 1011 1000 0101
But the actual value of the product is -0.222221777778. Therefore precision loss is involved in this Multiplication and is found to be 3.60644E-12 which is less than the resolution of Q31 representation i.e. 2-31. Thus it Provides 32 bit accurate products which is acceptable for most Of the DSP applications. For Q63 format multiplication as shown in fig. 7.
Input1=0.75=000011111111000011110000111100001111000011110000111100 0011110000
Input 2= 0.25=101010101010101010101010101010101010101010101010101010 1010101010
Output=0.1875=1010000010100000101000001010000010100000101000001010000010011111010111110101111101
0111110101111101011111010111110101111101100000

B.RTL Schematics for Q-format Multipliers:
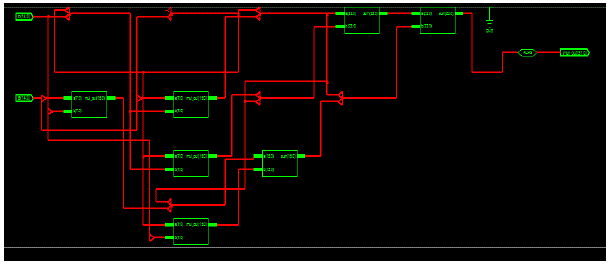
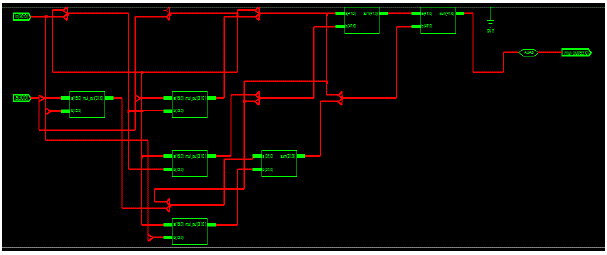
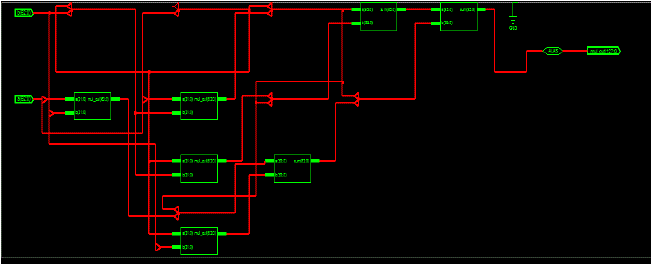
Fig.11.The outputs of 8X8 bit multipliers are added accordingly to obtain the 32 bits final product. Thus, in the final stage two adders are also required. The implemented RTLView of 16x16 bits Q-format Multiplier by using 8x8 blocks with the help of ModelSim Tool 6.1e.
Fig.12.The outputs of 16X16 bit multipliers are added accordingly to obtain the 64 bits final product. Thus, in the final stage two adders are also required. The implemented RTL View of 32x32 bits Q-format Multiplier by using 16x16 blocks with the help of ModelSim Tool 6.1e.
Fig.13.The outputs of 32X32 bit multipliers are added accordingly to obtain the 128 bits final product. Thus, in the final stage two adders are also required. The implemented RTL View of 64x64 Q-format Multiplier by using 32x32 blocks with the help of ModelSim Tool 6.1e.
It can be clearly noted from Table.1. That in terms of speed, the compressor based Urdhwa tiryakbhyam performs exceptionally well and is almost 1.39 times faster than the existing Urdhwa tiryakbhyam.
It can be clearly noted from Table.2.that in terms of speed, the compressor based Urdhwa tiryakbhyam performs exceptionally well and is almost 1.39 times faster than the existing Urdhwa tiryakbhyam.
It can be clearly noted from Table.3.that in terms of speed; the compressor based Urdhwa tiryakbhyam performs exceptionally well and is almost 1.19 times faster than the existing Urdhwa tiryakbhyam.
From table1, table2, table3 it can be clearly noted that in terms of area and time delay proposed compressor based Urdhwa tiryakbhyam gives good performance compare with Urdhwa tiryakbhyam method because by using compressor we are reducing the number of operations comparing with adders. Compressors are also used in multiplier architectures. Multipliers are structured into three functions: Partial-product generation, Partial-product accumulation and Final addition. The main source of power, delay and area came from the partial-product accumulation stage Compressors usually implement this stage because they contribute to the reduction of the partial products (reducing the number of adders at the final stage) and also contribute to reduce the critical path which is important to maintain the circuit's performance. As per the requirements we are increasing the compressor sizes (4-2compressor, 5-2 compressor etc) it gives maximum good performance.

CONCLUSION AND FUTURE WORK
The proposed fast multiplier architecture for signed Q-format multiplications using compressor based Urdhava Tiryakbhyam method of Vedic mathematics. Since Q-format representation is widely used in Digital Signal Processors. The proposed compressed Urdhava Tiryakbhyam method can substantially speed up the multiplication operation which is the basic hardware block. They occupy less area and faster than the Urdhava Tiryakbhyam method. Therefore the compressed Urdhava Tiryakbhyam Q-format multiplier is best suited for digital signal processing applications requiring faster multiplications. As a future work, the multiplier’s performance could be tested within an ALU and also compared with several other existing multipliers.

ACKNOWLEDGMENT
D.srinu would like to thank Mr. S.Rambabu, Assistant professor ECE Department who had been guiding throughout the project and would like to thank Mr.G.Leennendra chowdary, Assistant professor ECE Department for supporting me in giving technical ideas about the paper and motivating me to complete the work efficiently and successfully.

Tables at a glance
Table icon Table icon Table icon
Table 1 Table 2 Table 3

Figures at a glance
Figure Figure Figure Figure Figure
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure Figure Figure Figure
Figure 6 Figure 7 Figure 8 Figure 9
Figure Figure Figure Figure
Figure 10 Figure 11 Figure 12 Figure 13

References