Keywords
|
| Optimal Power Flow, Loss Minimization ,Particle Swarm Optimization , Improved Particle Swarm Optimization |
I. INTRODUCTION
|
| Optimal power flow is one of nonlinear constrained and occasionally combinatorial optimization problems of power systems. The various algorithms for solving such problems can be found in the literature. The optimal power flow problem has been developed continually since its introduction by Carpentier in 1962[1] . It is useful to determine the goals of optimal power flow problems. The primary goal of a generic optimal power flow is to minimize the total production costs of the entire system to serve the load demand for a particular power system while maintaining the security of the system operation. The production costs of electrical power systems may depend on the situation, but in general they normally mean to the cost of generating power at each generating unit of power plants. This operation is subjected to keep each device in the power system within its desired operation range at steady-state. This will include maximum and minimum outputs for generators, maximum MVA flows of power transmission lines and transformers, as well as system bus voltages within specified ranges. |
| It has taken over decades to develop efficient algorithms for its solution because it is a very large, non-linear mathematical programming problem. Many different mathematical approaches have been applied for seeking its solution. The methods discussed in the literature use one of the following five methods[2] . They are i) lambda iteration method as found in economic dispatch problem solving, ii) gradient method, iii) Newton’s method, iv) linear programming and v) interior point method. Apart from analytical approaches, there also exist heuristic search methods. |
| PSO- Heuristic search methods (e.g. simulated annealing ,genetic algorithm , evolutionary programming , particle swarm optimization[4] , etc) have been recently released for the optimal power flow problem. The genetic algorithm (GA) based solution methods are found to be most suitable because of their ability of simultaneous multidimensional search for optimal solution. They are well-known and widely used at the beginning period of solving the optimal power flow problems based on heuristic search methods. However, recent literatures show some deficiency of GA-based methods, newly developed heuristic approaches called particle swarm optimization (PSO) has been introduced[7] . This method combines social psychology principles and evolutionary computation to motivate the behaviour of organisms such as fish schooling, bird flocking, etc. PSO has been discovered to have better convergence performances than GAs . The PSO based method is based on a metaphor of social interaction. It searches a space by adjusting the trajectories of individual vectors, called ‘particles’ of a swarm, as they are conceptualized as moving as points in multidimensional space .The individual particles are drawn stochastically towards the positions of their own previous best performances and the best previous performance of the entire swarm. |
| This paper proposes an application of PSO and improved PSO to solve optimal power flow problems. The controllable system quantities are generator MW, controlled voltage magnitude, reactive power injection from reactive power sources and transformer tapping. The objective use herein is to minimize the power transmission loss by optimizing the control variables within their limits.Therefore, no violation on other quantities (e.g. MVA flow of transmission lines, load bus voltage magnitude, generator MVAR) occurs in normal system operating conditions. The proposed improved based method has been tested on a 30-bus test system and compared with the PSO based method. |
| This paper organizes a total of four sections. Next section,Section I illustrates optimal power flow problems with corresponding mathematical expressions of its objective and various practical constraints. Section II gives the brief of two |
| heuristic search methods, PSO and IPSO for comparative purposes. It also provides the algorithm procedure, described step-by-step. Section III is the simulation results and discussion. Conclusion remark is in Section IV. |
II. OPTIMAL POWER FLOW PROBLEMS
|
A. Problem Formulation
|
| The optimal power flow problem is a nonlinear optimization problem. It consists of a nonlinear objective function defined with nonlinear constraints. The optimal power flow problem requires the solution of nonlinear equations, describing optimal and/or secure operation of power systems. The general optimal power flow problem can be expressed as a constrained optimization problem as follows. |
| Minimize f(x) |
| Subject to g(x) = 0, equality constraints |
| h(x) ≤ 0, inequality constraints |
| By converting both equality and inequality constraints intopenalty terms and therefore added to form the penalty function. |
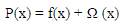 |
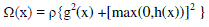 |
| Where |
| P(x) is the penalty function |
| Ω (x) is the penalty term |
| ρis the penalty factor |
| By using a concept of the penalty method , the constrained optimization problem is transformed into an unconstrained optimization problem in which the penalty function as described above is minimized. |
B. Objective Function
|
| Although most of optimal power flow problems involve the total production cost of the entire power system, in some cases some different objective may be chosen. In this paper, the power transmission loss function is set as the objective function. The power transmission loss can be expressed as follows. |
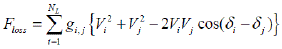 |
| Where Vi is the voltage magnitude at bus i |
| gi,j is the conductance of line i-j |
| δ i is the voltage angle at bus i |
| NL is the total number of transmission lines |
C. System Constraints
|
| The controllable system quantities are generator MW, controlled voltage magnitude, reactive power injection from reactive power sources and transformer tapping. The objective use herein is to minimize the power transmission loss function |
| by optimizing the control variables within their limits. Therefore , no violation on other quantities (e.g. MVA flow of transmission lines, load bus voltage magnitude, generator MVAR) occurs in normal system operating conditions. These are system constraints to be formed as equality and inequality constraints as shown below. |
| 1) Equality constraint: Power flow equations |
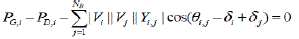 |
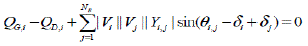 |
| Where PGi is the real power generation at bus i |
| QGi is the reactive power generation at busi |
| PDi is the real power demand at bus i |
| QDi is the reactive power demand at bus i |
| NB is the total number of buses |
| Θi,jis the angle of bus admittance element i,j |
| Yi,j is the magnitude of bus admittance elementi,j |
2) Inequality constraint: Variable limitations
|
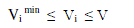 |
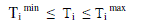 |
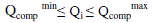 |
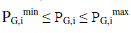 |
| Where |
| Vi min , Vi max are upper and lower limits of voltage magnitude at bus i |
| Ti min , Ti max are upper and lower limits of tap position of transformer i |
| Qcomp min, Qcomp max are upper and lower limits of reactive power source i |
| PG,i min , PG,i max are upper and lower limits of power generated by generator i The penalty function can be formulated as follows |
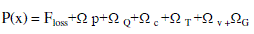 |
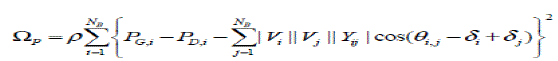 |
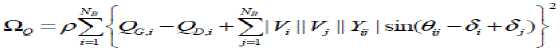 |
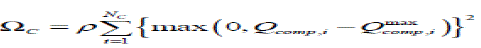 |
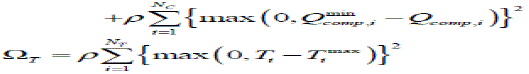 |
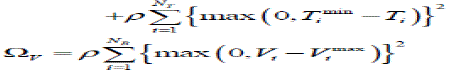 |
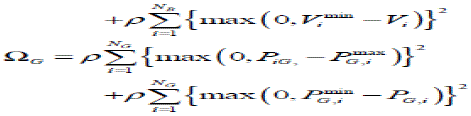 |
| NG is the total number of generators |
| NC is the total number of reactive power sources |
| NT is the total number of transformers |
III. INTELLIGENT SEARCH METHODS
|
A. Particle Swarm Optimization (PSO)
|
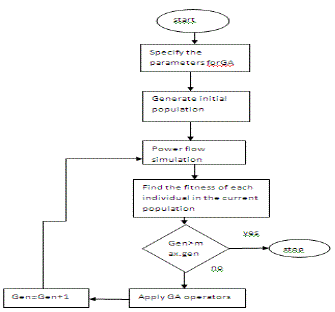
| Kennedy and Eberhart developed a particle swarm optimization algorithm based on the behaviour of individuals (i.e., particles or agents) of a swarm . Its roots are in zoologist’s modelling of the movement of individuals (i.e., fish ,birds, and insects) within a group. It has been noticed that members of the group seem to share information among them to lead to increased efficiency of the group. The particle swarm optimization algorithm searches in parallel using a group of individuals similar to other AI-based heuristic optimization techniques. Each individual corresponds to a candidate solution to the problem. Individuals in a swarm approach to the optimum through its present velocity, previous experience, and the experience of its neighbors. In a physical n-dimensional search space, the position and velocity of individual i are represented as the velocity vectors. Using these information individual i and its updated velocity can be modified under the following equations in the particle swarm optimization algorithm. |
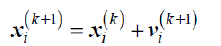 |
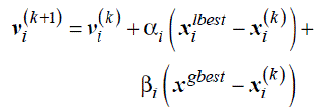 |
| Where |
| x i k is the individual i at iteration k |
| vi k is the updated velocity of individual i at iteration k |
| αi , βi are uniformly random numbers between [0,1] |
| xi lbest is the individual best of individual i |
| xi g best is the global best of the swarm |
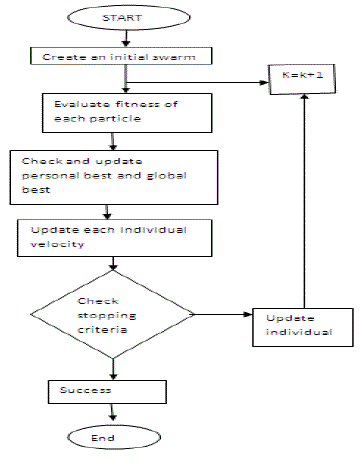
| The procedure of the particle swarm optimization can be summarized in the flow diagram of Fig. 1. |
B . Improved Particle Swarm Optimization (IPSO)
|
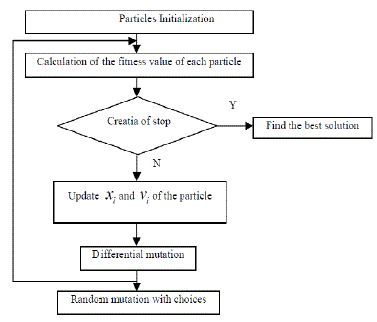
| Improved PSO introduces differential mutation and random mutation to increases the diversity of particles group. The performances of algorithms are evaluated using the following standards .1) Evaluation of convergence rates 2) Evaluation of stability and quality of convergence. |
C . Genetic Algorithm (GA)
|
| There exist many different approaches to adjust the motor parameters. The GA is well-known [9] there exist a hundred of works employing the GA technique to identify system parameters in various forms. The GA is a stochastic search technique that leads a set of population in solution space evolved using the principles of genetic evolution and natural selection, called genetic operators e.g. crossover, mutation, etc. With successive updating new generation, a set of updated solutions gradually converges to the real solution. Because the GA is very popular and widely used in most research areas where an intelligent search technique is applied, it can be summarized briefly as shown in the flowchart of Fig. 1 . |
IV. SIMULATION RESULTS
|
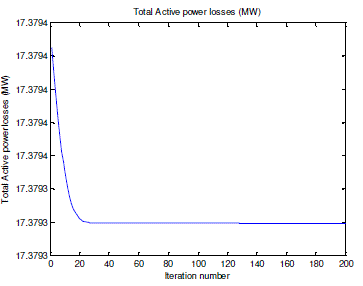
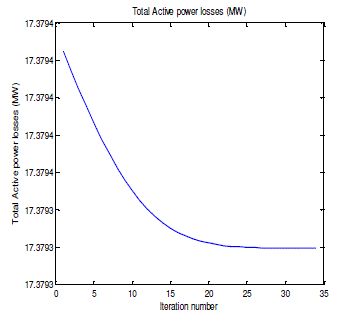
| To verify the effectiveness of the proposed particle swarm optimization, a 30-bus test power system was tested. Information of the test power system is given in TABLE I. The simulations were performed using MATLAB software . The test was carried out by solving the optimal power flow problem of the power loss objective in which variable limits as given in TABLE II are used as system constraints. For comparison purposes, Newton’s Method, particle swarm optimization and improved particle swarm optimization were applied to solve this test case. Each method was challenged by solving a given optimal power flow problem of 30 trials randomly. Also, convergence characteristics of the PSO-based optimal power flow solution are depicted in Fig. |
V. CONCLUSION
|
| Solution methods for solving optimal power flow problems with the power transmission loss objective are described in this paper. Some efficient search methods (Newton method , particle swarm optimization and improved particle swarm optimization) are employed. A 30-bus power system was established as a test case for benchmarking. The results showed that a set of optimal solutions with respect to the power transmission loss objective can be efficiently found. As a result, the IPSO method proves that it can find a place among some efficient search methods in order to find a near global solution of the optimal power flow problems. |
| |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
| |
References
|
- M.R AlRashidi and M.E El-Hawary, “Hybrid Particle Swarm Optimization Approach for Solving the Discrete OPF Problem Considering theValve Loading Effects”, IEEE Transactions on Power Systems, Issue 4, Vol. 22, pp.2030 – 2038, 2007.
- B. Zhao, C.X. Guo and Y.J. Cao, “Improved particle swam optimization algorithm for OPF problems”, IEEE-PES Power SystemsConference and Exposition,Vol. 1, pp.233 - 238, 10-13 October 2004.
- L. Weibing, L. Min and W. Xianjia, “An improved particle swarm optimization algorithm for power flow”, IEEE 6th International PowerElectronics and Motion Control Conference 2009, pp. 2448 – 2450, 17-20 May 2009.
- C. Gonggui and Y. Junjjie, “A new particle Swarm optimizationSolution to Optimal reactive power flow problem’’,Asia- Pacific Power andEnergy Engineering conference,pp1-4,27-3 March 2009.
- W. Cui-Ru, Y. He-Jin, H. Zhi-Qiang, Z. Jiang- Wei and S.chen, “A modified particle swarm optimization algorithm and its application inoptimal power flow problem”, International conference Machine Learning and Cybernetics 2005, pp. 2885 August 2005.
- S. M. Kumari, G. Priyanka and M. Sydulu ,”comparison of Genetic Algorithms and Particle Swarm Optimization for Optimal Power FlowIncluding FACTS devices”, IEEE poweTech 2007, pp. 1105 - 1110, 1-5 July 2007.
- M.A. Abido, “Multi objective particle swarm optimization for optimal power flow problem”, 12th International Middle-East Power SystemConference , pp. 392 – 396, 12-15 March 2008.
- S.P Karthikeyan, K. Palanisamy, L.J. Varghese, I.J. Raglend and D.P. Kothari, “Comparison of Intelligent techniques to Solve EconomicLoad Dispatch Problem with Line Flow constrints,” IEEE International Advance Computing conference 2009 pp. 446 – 452, 6-7 March 2009
- P. Dutta and A. K. Sinha, “Voltage Stability Constrained Multi- objective Optimal Power Flowusing Particle Swarm optimization, 1stInternational Conference on Industrial and information Systems, pp. 161 – 166, 8-11 August 2006.
|