Keywords
|
| |
| Small signal Stability, Heffron-Phillips model, Low frequency oscillations (LFO), Power system stabilizers (PSS), PI Controller, Fuzzy logic controller, Hybrid fuzzy logic damping controller(HFLDC), Single machine infinite bus (SMIB) power system, Static synchronous series compensator (SSSC). |
| |
INTRODUCTION
|
| |
| Todays, large interconnected power systems are operating to their stability limits for reliable and economical operation. However, low frequency oscillations (LFO) with the frequencies in the range of 0.1 to 2 Hz are one of the direct results of the large interconnected power systems. If these oscillations are not damped they make the interconnected system vulnerable to the risk of instability. These oscillations may come up to the overall rated capacity of a transmission line due to their superimposed effect on steady state line flow. Hence, the oscillations would limit the total and available transfer capability (TTC and ATC) by requiring higher safety margins. Thus, in order to maintain the stability of the entire system, it is urgent to damp the electromechanical oscillations as soon as possible [1]. |
| Traditionally, Power System Stabilizers (PSS) have been employed as the first choice to mitigate these problems. However, performance of PSS gets affected by network configurations, load variations etc. Hence installations of FACTS devices have been suggested in this paper to achieve appreciable damping of system oscillations. This has initiated a new and more versatile approach to control the power system in a desired way [4]. FACTS controllers provide a set of interesting improvements including power flow control, reactive power compensation, voltage regulation, damping of oscillations [5]-[12]. |
| The static synchronous series compensator (SSSC) is one of the series FACTS devices based on a solid-state voltage source inverter (VSC) which generates a controllable ac voltage in quadrature with the line current [13]. By this way, the SSSC emulates as an inductive or capacitive reactance and hence controls the power flow in the transmission lines. In [14], authors have developed the damping function for the SSSC. It is a well-known fact that by properly designing POD controller, the SSSC would be capable of suppressing the fluctuations as an extra duty [14]. |
| SSSC damping controller can be designed using various methods, for example, in [14] authors have used the phase compensation method. The main problem associated with these methods is that the control process is based on the linearized machine model. The other mostly used method is the proportional-integral (PI) controller. Even though the PI controllers offer simplicity and ease of design, its performance deteriorate when the system conditions vary widely or large disturbances occur [15]-[16]. |
| In this research, some new stabilizing control solutions for power system have been presented. Recently, fuzzy logic controllers (FLCs) have emerged as an efficient tool to avoid these drawbacks. Most of fuzzy logic systems encode human reasoning into a program in order to arrive at decisions or to control a system [17]-[18]. Fuzzy logic comprises fuzzy sets, which is a way of representing non-statistical uncertainty along with approximate reasoning and in fact includes the operations used to make inferences [19]. In [20], Limyingcharone et al. have used a fuzzy supplementary controller with the aim of achieving low frequency oscillations damping |
| The main contribution of this paper is to addresses the design of a hybrid fuzzy damping controller to attenuate LFO by SSSC. The investigation is carried out for a single machine infinite bus (SMIB) power system installed with a SSSC. In the sequel, the linearized Heffron-Phillips model [16] of the examined plant is evolved. A hybrid fuzzy damping controller is utilized to modulate the amplitude modulation index during the transients to enhance the stability of the power system. Subsequently, aiming to provide a fruitful investigation, a comparative study is developed where the hybrid fuzzy damping controller is compared with a conventional fuzzy logic controller and PI controller. Simulation results using MATLAB/Simulink exhibits the superior damping of LFO obtained with hybrid fuzzy damping controller than conventional fuzzy logic controller and conventional PI controller. |
SYSTEM MODEL
|
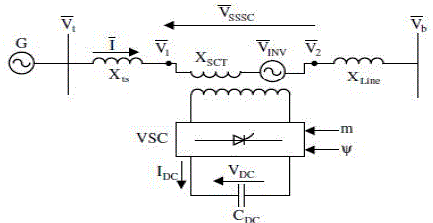
| A single machine infinite bus installed with SSSC is as shown in Fig1. Here Xts is transformer reactance and XLine corresponds to the reactance of the transmission line. Also Vt and Vb represents generator terminal voltage and infinite bus voltage respectively. For the SSSC, XSCT is the transformer leakage reactance; VINV is the series injected voltage; CDC is the DC link capacitor; VDC is the voltage at DC link; m is the amplitude modulation index and ψ is the phase angle of the series injected voltage. |
A. NONLINEAR DYNAMIC MODEL OF THE POWER SYSTEM WITH SSSC:
|
| Initially a nonlinear dynamic model for the examined system is derived by neglecting the resistance of all the components including generator, transformer, transmission line, and series converter transformer. The equations specifying the dynamic performance of the SSSC can be written as follows [14]. |
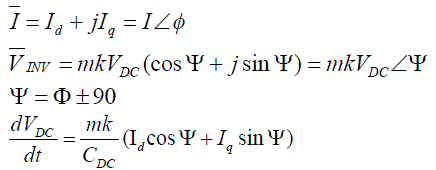 (1) (1) |
| |
| Where ‘k’ is the fixed ratio between the converter AC and DC voltages and is dependent on the inverter structure. For a simple three-phase voltage source converter k is equal with 3/4 [4]. Most of the times, SSSC performs as a pure capacitor or inductor; hence, the only main controllable parameter for SSSC is the amplitude modulation index m. |
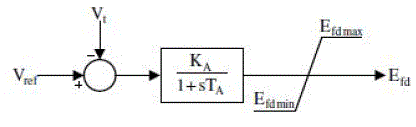
| In the analysis a IEEE Type-ST1A excitation system is considered. Fig. 2 displays the block diagram of the excitation system where the terminal voltage Vt and the reference voltage Vref are the input signals. KA and TA are the gain and time constant of the excitation system respectively. |
| The dynamic model of the power system in fig. 1 would be as follows [22] |
| |
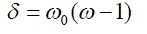 |
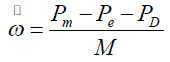 |
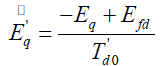 |
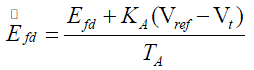 |
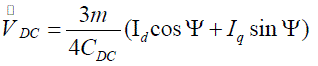 |
| Where |
| δ : Rotor angle of synchronous generator in radians |
| ω : Rotor speed in Radians per second |
| PM : Mechanical power input to the generator |
| PE : Electrical power of the generator |
| P =D (ïÃÂ÷ ïÃâ¬ÃÂ1) : Damping coefficient |
| 'qE :` Generator internal voltage |
| fd E : Generator field voltage |
| Id : d-axis current |
| Iq : q-axis current |
| |
B. LINEAR DYNAMIC MODEL OF THE POWER SYSTEM WITH SSSC:
|
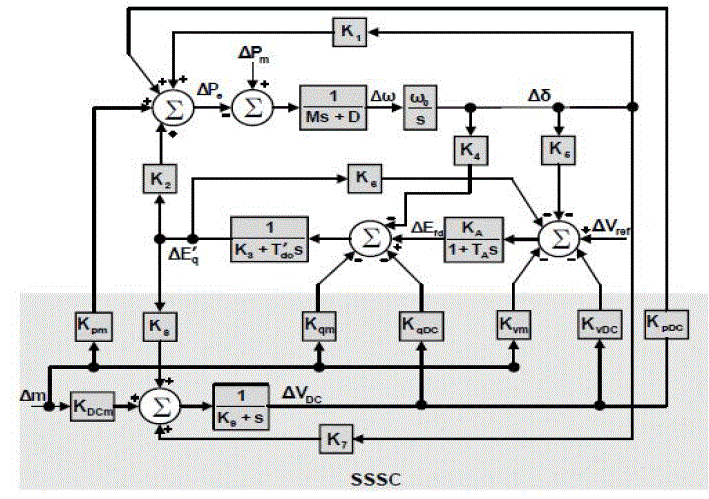
| The linear Heffron-Philips model of an SMIB system including SSSC can be extracted by linearizing the nonlinear model around a nominal operating point [14]. |
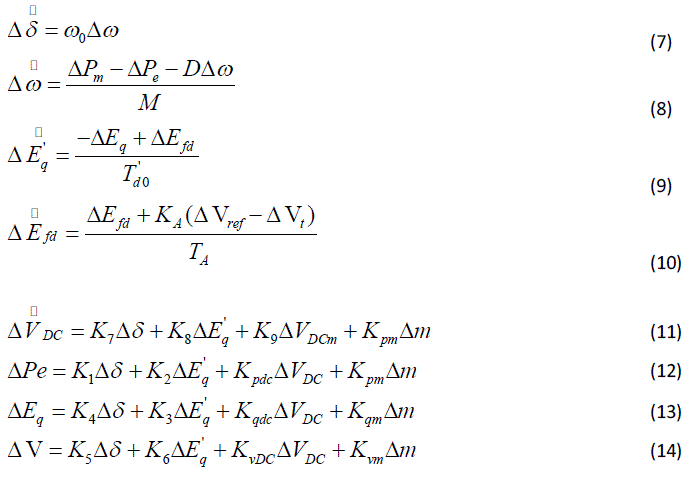 |
| |
| Fig. 3 exhibits the transfer function model for the modified Heffron-Phillips model of the SMIB system with SSSC. |
C. STATE SPACE REPRESENTATION OF LINEAR MODEL
|
| The modified Heffron-Phillips model can be represented as: |
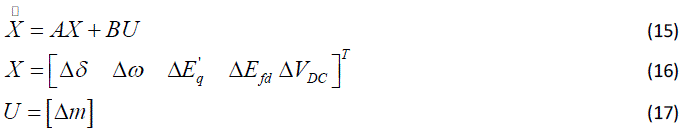 |
| With respect to (7)-(15), the corresponding system matrix namely A, and the control matrix namely B, are obtained for the investigated power system. |
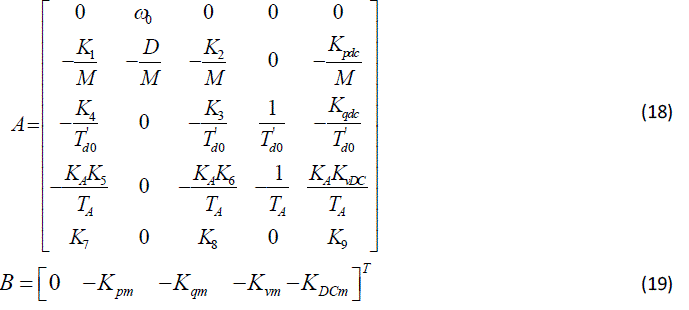 |
| |
D. CALCULATION OF THE HEFFRON-PHILLIPS MODEL CONSTANTS
|
| The nominal operating point for the power system is set to the given values. |
| Pe = 0.8 pu, Qe = 0.144 pu, Vb = 1pu |
| The Heffron-Phillips model constants are calculated based on the given values for the nominal operating point |
DAMPING CONTROLLERS DESIGN AND ITS PERFORMANCE
|
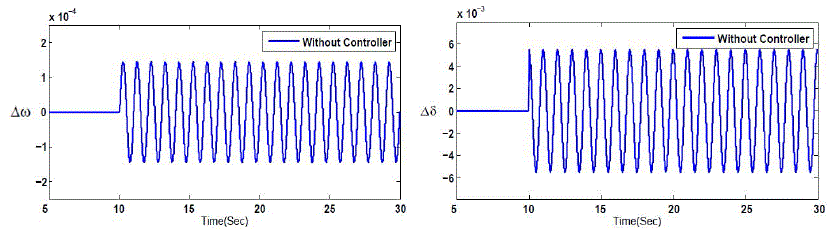
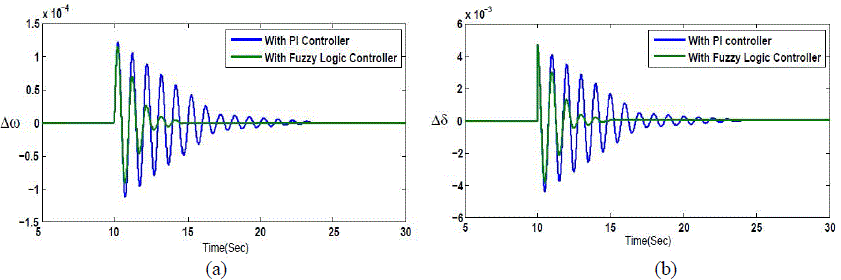
| In this investigation three types of damping controllers are designed and compared. Controllers will develop amplitude modulation index for the SSSC for damping oscillations. For the sake of analysis a step change is considered as the contingency in mechanical power (Δ Pm = 0.01) which occurs at t=10 sec and lasts for 0.1 sec. At the beginning, the SSSC has no damping controller. The angular velocity deviation and also the load angle deviation responses are displayed in Figure 4 (a) and (b) respectively. This figure reveals that when the system has no damping controller, there is a very poor damping in LFO; hence an auxiliary damping controller is essentially required to improve the small signal stability of the system. |
A. CONVENTIONAL PROPORTIONAL-INTEGRAL (PI) CONTROLLER
|
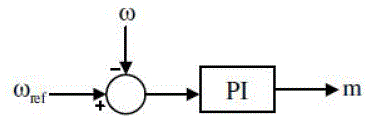
| The damping controllers are designed so as to provide an extra electrical torque in phase with the speed deviation in order to enhance the damping of oscillations. Fig. 5 shows the conventional PI controller structure. With respect to this figure, it can be observed that the first block compares the generator rotor speed with the reference speed. In the sequel, the error is fed to a PI controller to generate the proper amplitude modulation index for the SSSC converter. There are different methods to design PI controllers such as trial and error method, pole-placement, Ziegler-Nichols and so forth. In this work, trial and error method is used to set suitable values for PI controller gains. |
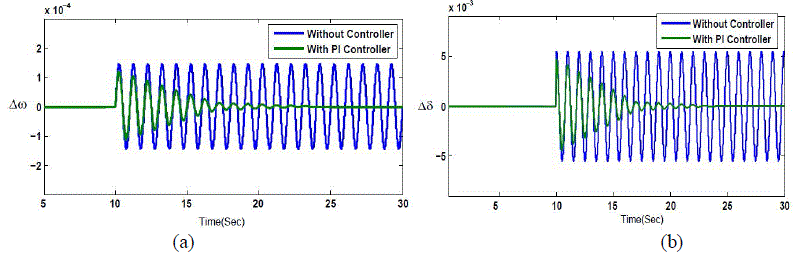
| Figure 6 demonstrates that by considering the PI controller, the oscillations are more effectively damped. The operation of this controller mainly depends on the operating point. For the changing operating conditions, this classic controller will not be as effective as for its initial operating point. |
B. FUZZY LOGIC DAMPING CONTROLLER
|
| |
| As explained in the preceding sections, although the classic controllers offer simplicity with an easy design, their performance depreciates when vide variations occur in the system conditions or large disturbances happen. Consequently, to ensure the effective performance of damping controller over wide range of system operations and also to increase the transient stability of the system, a supplementary fuzzy logic controller (FLC) based on the Mamdani's fuzzy inference method is designed for the SSSC input. FLC generates the required small change for amplitude modulation index to control the magnitude of the injected voltage. The centroid defuzzification technique was used in this fuzzy controller |
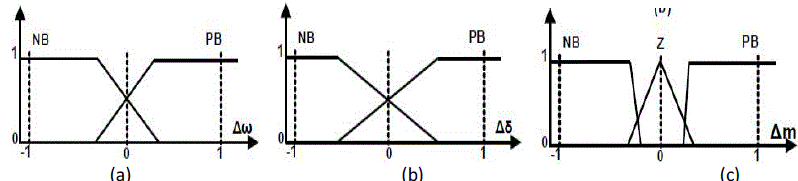
| Fig. 7 demonstrates the FLC structure. In this case, a two–input, one–output FLC is considered. The input signals are angular velocity deviation (Δω ) and load angle deviation (Δδ ) and the resultant output signal is the amplitude modulation index (Δm) for SSSC converter. K1 and K2 are the input scaling factors to scale the input signals in the range of [-1,1]; and Ko is the output scaling factor to scale the output to the real values. The presented FLC has a very simple structure. The membership functions of the input and output signals are shown in Figure 8 (a), (b) and (c) respectively. There are two linguistic variable for each input variable, including, “Positive” (P), and “Negative” (N). On the other hand, for the output variable there are three linguistic variables, namely, “Positive” (P), “Zero” (Z), and “Negative” (N). The rules used for the FLC are chosen as follows: |
| 1. If Δω is P and Δδ is P, then is P. |
| 2. If Δω is P and Δδ is N, then is Z. |
| 3. If Δω is N and Δδ is P, then is Z. |
| 4. If Δω is N and Δδ is N, then is N. |
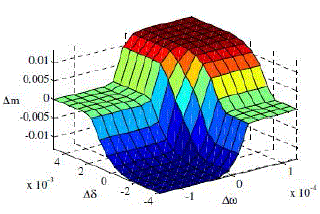
| Fig. 9 demonstrates the output of fuzzy controller versus its inputs. As it can be seen in Fig. 9, the rules surface is smooth which a desirable method fuzzy controller is. |
| In this case, simulations are performed with the same contingency in mechanical power but the SSSC has been equipped with a damping controller. Simulation results are shown in Fig. 9 (a) & (b). With respect to this figure, it is deduced that the fuzzy logic controller exhibits better damping than the conventional PI controller. Likewise, the power system transient stability is increased when the SSSC is equipped with the fuzzy logic damping controller. Simulation results validate the efficiency of the proposed fuzzy logic damping controller and its better performance is emphasized. |
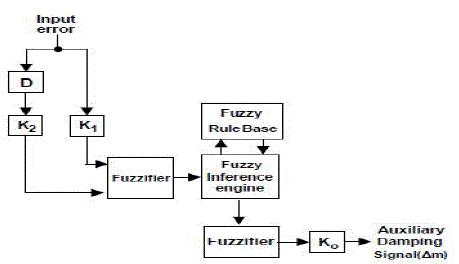
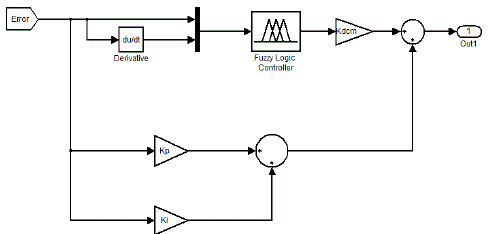
C. HYBRID FUZZY LOGIC DAMPING CONTROLLER
|
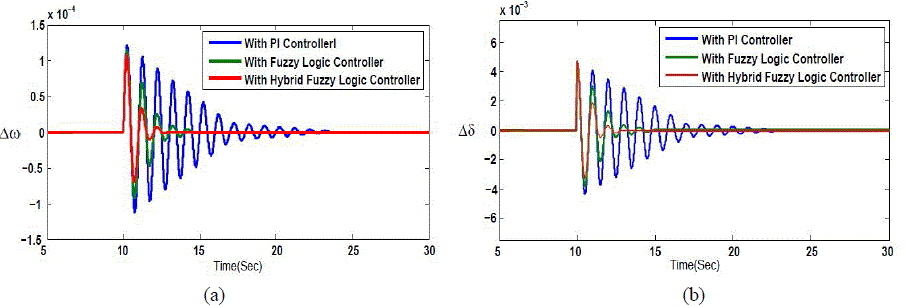
| It is a combination of conventional fuzzy logic damping controller (FLDC) and conventional PI controller. The internal structure of the hybrid fuzzy damping controller is shown in the Fig. 10. The same structure used in above Fig 7 is used in the fuzzy logic controller. Performance of HFLDC in low frequency oscillations is shown in Figure 11 where the best damping performance is deduced for this controller among the previously examined. HFLDC provides more reliability and covers a wide range of operating points. |
CONCLUSION
|
| This paper serves an exact investigation to obtain a complete linearized Heffron-Phillips model SMIB power system equipped with an SSSC to study LFO damping with an FLDC. It was shown that a contingency in power system will cause to initiate power oscillations. In the sequel, three types of controllers, namely, the PI, FLDC and HFLDC were designed to damp the system oscillations. A comparative study between these controllers shows that the proposed HFLDC has superior performance and influence in transient stability enhancement and oscillations damping. Simulation results show the efficiency of the proposed HFLDC and its better performance in damping the low frequency oscillations among the studied controllers. |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
 |
 |
| Figure 11 |
Figure 12 |
|
References
|
- P. Kundur. Power system stability and control . Prentice-Hall,N. Y, U. S. A, 1994.
- E. V. Larsen and D. A. Swann, “Applying power system stabilizers, P-III, practical considerations,” IEEE Trans. Power App. Syst ., vol. 100, no.6, pp. 3034–3046, Dec. 1981.
- X. Lei, E. N. Lerch, and D. Povh, “Optimization and coordination of damping controls for improving system dynamic performance,” IEEE Trans.Power Syst. , vol. 16, pp. 473–480, Aug. 2001.
- N.G. Hingorani, L. Gyugyi, Understanding FACTS: Concepts and technology of flexible ac transmission system, IEEE Press, NY, 2000.
- J.G. Douglas, G.T. Heydt, “Power Flow Control and Power Flow Studies for Systems with FACTS Devices,” IEEE Trans. Power Syst, vol. 13,No. 1, 1998, pp. 60-65.
- H. Taheri, S. Shahabi, Sh. Taheri, A. Gholami “Application of Static Synchronous Series Compensator (SSSC) on Enhancement of VoltageStability and Power Oscillation Damping ,” IEEE Conf , pp. 533 – 539, 28 Sept-1 Oct, 2009.
- E.V. Larsen, J.J. Sanchez-Gasca, J.H. Chow, and “Concepts for Design of FACTS Controllers to Damp Power Swings”, IEEE Trans. Power Syst, Volume: 10, Issue: 2, pp. 948-956, May 1995.
- M. S. El-Moursi, B. Bak-Jensen, M. H. Abdel-Rahman “Novel STATCOM Controller for Mitigating SSR and Damping Power SystemOscillations in a Series Compensated Wind Park,” IEEE Trans. Power Delivery. , vol. 25, no. 2, pp. 429–441, Feb 2010.
- R. K. Varma, S. Auddy, and Y. Semsedini, “Mitigation of subsynchronous resonance in a series-compensated wind farm using FACTScontrollers,” IEEE Trans. Power Del., vol. 23, no. 3, pp. 1645–1654, Jul. 2008.
- R.M. Mathur and R.K. Varma, Thyristor-Based FACTS Controllers for Electrical Transmission Systems . IEEE Press and Wiley Interscience,New York, USA, Feb. 2002.
- 11. R. Majumder, B. C. Pal, C. Dufour, and P. Korba, “Design and realtime implementation of robust FACTS controller for damping interareaoscillation,” IEEE Trans. Power Syst., vol. 21, no. 2, pp. 809–816, May 2006.
- A. Prasai and D. M. Divan, “Zero-energy sag correctors optimizing dynamic voltage restorers for industrial applications,” IEEE Trans. Ind.Appl. , vol. 44, no. 6, pp. 1777–1784, Nov./Dec. 2008.
- L. Gyugyi, C. D. Schauder, and K. K. Sen, “Static synchronous series compensator: A solid-state approach to the series compensation oftransmission lines,” IEEE Trans. Power Del. , vol. 12, no. 1, pp. 406–417, 1997.
- H.F. Wang, “Design of SSSC damping controller to improve power system oscillation stability,” AFRICON, IEEE, Vol. 1, pp. 495 – 500, 28Sept-1 Oct, 1999.
- A: P. K. Dash, S. Mishra, and G. Panda, “Damping multimodal power system oscillations using a hybrid fuzzy controller for series connectedFACTS devices,” IEEE Trans. Power Syst ., vol. 15, No. 4, pp. 1360–1366, Nov. 2000.
- Z. Huaang, Y. X. Ni, C. M. Shen, F. F.Wu, S. Chen, and B. Zhang, “Application of unified power flow controller in interconnected powersystems modeling, interface, control strategy, and case study,” IEEE Trans. Power Syst ., vol. 15, pp. 811–816, May 2000.
- Cornelius T. Leondes, Fuzzy Therory Systems: Techniques and Applications , San Diego, Calif. Academic Press, London, 1999.
- Michio Sugeno, Hung T. Nguyen and Nadipuram R. Prasad, Fuzzy Modeling and Control: Selected Works of M. Sugeno , CRC Press, BocaRaton, 1999.
- Hao Ying, Fuzzy Control and Modeling: Analytical Foundations and Applications , IEEE Press Series on Biomedical Engineering, SeriesEditor: Metin Akay, New York, 2000.
- S. Limyingcharone, U. D. Annakkage, and N. C. Pahalawaththa, “Fuzzy logic based unified power flow controllers for transient stability improvement,” IEE Proc. C , vol. 145, no. 3, pp. 225–232, 1998.
|