Keywords
|
| 1D Bar codes, 2D Matrix codes, RS codes, Finite Fields, color coding. |
INTRODUCTION
|
| Information codes are used to convey information about a product. For this purpose barcodes are being used. Bar code is a fast, easy, accurate and automatic data collection method. Barcode enables products to be tracked proficiently and exactly at speeds not possible using manual data entry systems. Barcode is formed by converting given information into binary form. Parity bits or checksum is added to the obtained binary data for error correction. In barcodes information will be in horizontal format and is present in the first row, as single row can`t be visible we repeat it into multiple rows. so every row contains same information. Maximum storage capacity of these codes is up to 20 characters only. |
| Now a days instead of barcodes QR codes are widely used because of their increased information storage capacity compared to barcodes. Here the information will be in horizontal and vertical format. Maximum storage capability of QR code using only two colors (black & white) is 4296 characters in version 40. This capacity can be further improved by considering more colors along with black and white i.e.; red, blue, green etc. or by using multiplexing technique. |
| This paper is planned as follows: Section 2 deals with Literature survey. Section 3 describes finite fields. Section 4 deals with RS codes. Followed by Section 5 with proposed algorithm and simulation results. The conclusion is specified in section 6. |
RELATED WORK
|
| Algorithms for encoding and decoding the QR codes are existing in the literature. During the years many have urbanized algorithms for QR codes, a few of them are Sartid Vongpradhip [1] proposed an algorithm to increase the capacity of QR code by using Multiplexing. Md. Wahedul Islam, Saif alZahir [2] proposed a novel QR code guided image stenographic technique. Yinghui Zhang, Tianlei Gao, Deguang Li, Huaqi Lin [3] proposed an algorithm to convert a gray image into binary image. Sartid Vongpradhip, Suppat Rungraungsilp[4] proposed an algorithm , how to use QR Code as Invisible Watermarking. Chun Jin and Jianghong Yuan, Leilei Li, Eryang Chen, Tao Tang[5] and Zhang Yongjun [6]proposed an algorithm to decode the information from the damaged QR coding by using RS error correction code. |
| sartid vongpradhip et al [1] proposed an novel algorithm use multiplexing to increase information in QR code, in the algorithm three messages are considered and individual QR code are generated, these three QR codes are multiplexed and formed into a group of three bits each bit from one QR code and these three bits are assign to a special character . at the final step instead of black or white square this special character is replaced. At decoder side each special character is read and corresponding group of three bits are obtained and those are again de-multiplexed to the individual QR code. |
FINITE FIELDS
|
| Reed-Solomon codes are error-correcting codes which are used all over today. Reed-Solomon codes be based on finite fields. Finite fields are also famous as Galois fields in honor of Evariste Galois, who was the first to revise these finite fields. |
| A field is a set of elements F for which addition, multiplication, subtraction and division performed with its elements upshot in another element of the same set. F is a commutative group with esteem to the addition operation. The identity element for the addition is ‘0‘. It is a commutative group for the multiplication operation. The identity element for multiplication is ‘1‘. Multiplication is distributive with respect to addition a(b + c) = ab + ac. The number of elements in a field is called the order of that field. The inverse for the addition operation of an element of the field a ∈ F is denoted as −a, and inverse for the multiplication operation of an element of the field is denoted as. Subtraction and division operations are defined as a function of the inverse elements as |
| a − b = a + (−b) |
| a/b = a(b-1 ) |
| The set = {0, 1} defined under addition and multiplication modulo 2 is such that ={0, 1} is a commutative group with respect to the addition operation, and is also a commutative group with respect to the multiplication operation. This is the so called binary field GF(2). Operations in this binary field are defined by table 1. |
| For the degree of then polynomial m=3 the primitive polynomial is 1+X+ X3 which defines a finite field GF(23). So there are 23 =8 elements in the field defined by f(X). The familiar binary elements 1 and 0 do not satisfy the polynomial f(x) = 1+X+ X3. Let x an element of extension field be defined as a root of the polynomial f(X). |
| Therefore it is possible to write |
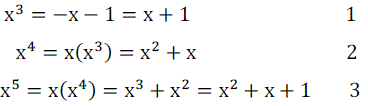 |
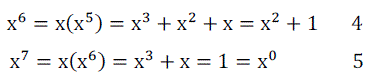 |
| Operations performed on finite fields are only addition and multiplication because subtraction is similar to addition and division is equal to multiplication of its inverse. |
| For example consider GF(23) |
| The elements are 0, xïÿýïÿý, x1, x2, xïÿýïÿý, x4, x5,xïÿýïÿý. |
| x0+x5=x4 x3+x4=x6 |
| so, in finite fields addition is nothing but xor operation. |
| x2 . x3=x 5 x5 . x6=x4 |
| so in finite fields multiplication is nothing but modular addition operation. |
REED SOLOMON CODES
|
| Reed Solomon codes have huge power and helpfulness, and are today found in several applications from dense disc players to external space applications. The Reed-Solomon codes (RS codes) are under the category of non binary cyclic codes with code symbols from a Galois field. They were bare in 1960 by I. Reed and G. Solomon. The work was finished when they were at MIT Laboratory. In the decades since their advance, RS codes have enjoyed innumerable applications from compact discs, digital TV in living room to spaceship and satellite in outer space. The most essential RS codes are codes with symbols from GF(2m). One of the most essential features of RS codes is that the minimum distance of an (n, k) RS code is n–k+1. Codes of this breed are called “maximum-distance-separable codes”. |
| The code is skilled of correcting any combination of t or fewer errors, where t can be expressed as |
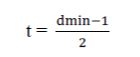 |
| The encoding process can be done in two ways one is division method and second is systematic method. |
| Division method: |
| – Multiply the non-binary message polynomial m(x) by xn-k |
| – Dividing xn-km(x) by g(x) to obtain the remainder b(x) |
| – Forming the codeword b(X)+xn-ku(x) |
| Systematic method: |
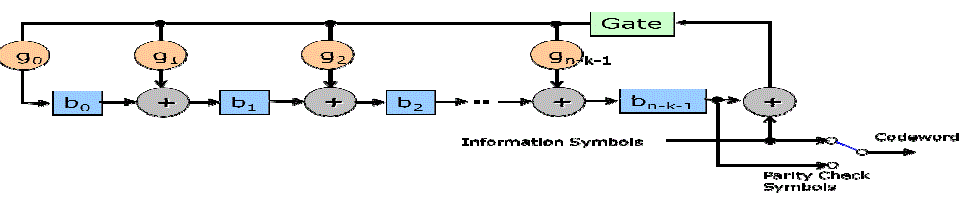
| Figure 1 shows the encoder circuit diagram. The registers b0, b1, b2……..bn-k-1 are initially filled with zeros. the information symbols are applied as input to the encoder circuit. After the last symbol of information symbols, the values contained in the set of registers will be considered as parity check symbols. |
| The procedure of the RS decoding algorithm can be decayed into four steps: |
| Step1: Calculate the syndrome vector. |
| Step2: Calculate the error location polynomial. |
| Step3: Calculate the roots of the error location polynomial. |
| Step4: Calculate the value of the error, and do the error correcting. |
ALGORITHM
|
| QR ENCODING ALGORITHM |
| 1. Enter the users data to generate the QR code |
| 2. Convert the entered data into its ASCII equivalent |
| 3. Using the ASCII equivalent Finite Fields Numbers are generated by using Primitive polynomial |
| 4. Codeword is generated for the Finite Field numbers using RS encoder algorithm |
| 5. The codeword is converted into its binary Equivalent |
| 6. These bits are placed according to the QR code pattern |
| 7. Each users QR code is considered as a color plane |
| 8. Combining the three color planes, colored QR is generated. |
| QR DECODING ALGORITHM |
| 1. Read the color QR code |
| 2. Split it into RGB planes |
| 3. For each plane eliminate the QR patterns |
| 4. These bits are grouped into 8 bit representation |
| 5. Convert the binary to decimal for each byte |
| 6. Apply to RS decoder as input |
| 7. The output of RS decoder are ASCII equivalents |
| 8. Converting them into characters gives the original information |
EXPERIMENTAL RESULTS AND DISCUSSIONS
|
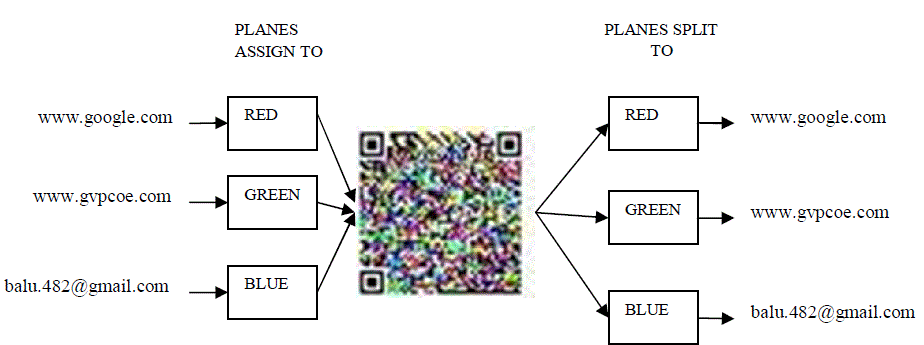
| In encoding process, three users information is considered and individual black and white QR code is generated. The black and white QR codes are assign to Red, Green and Blue planes, combining these three planes, color QR code is generated. Similarly, in decoding side colored QR code is split into individual planes (Red, Green and Blue) and decode the information from each plane as shown in below figure. |
| The capacity of black and white QR code is up to 233 characters for 48x48 module size. The capacity is increased 3 times of present QR code by considering Red, Green and Blue planes as shown in table 2. |
CONCLUSION
|
| In the proposed algorithm multiplexing technique along with basic QR code generation algorithm, color QR code is generated. Thus the capacity of the Quick Response code is increased by considering the color coding technique instead of basic QR code algorithm. This algorithm increases the QR code capacity by 3 times compared to the present black and white QR codes. QR code damaged up to 30% can be efficiently decoded using RS codes. The capacity can be further increased by considering each QR code in terms of bit planes. |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2a |
|
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
References
|
- SartidVongpradhip ,”Use Multiplexing to Increase Information in QR Code”, The 8th International Conference on Computer Science & Education,IEEE, pp. 361-364, 2013.
- Md. Wahedul Islam, SaifalZahir,” A Novel QR Code Guided Image Stenographic Technique”, IEEE International Conference on ConsumerElectronics, pp. 586-587, 2013.
- Yinghui Zhang, TianleiGao, Deguang Li, Huaqi Lin,” An Improved Binarization Algorithm of QR Code Image”,IEEE, pp.2376-2379, 2012.
- SartidVongpradhip, SuppatRungraungsilp,” QR Code Using Invisible Watermarking in Frequency Domain”, IEEE, Ninth International Conferenceon ICT and Knowledge Engineering , pp.47-52, 2011.
- Chun Jin and Jianghong Yuan, Leilei Li, Eryang Chen, Tao Tang,” Optimization of RS Error-Correcting Decoding Algorithm for QR Code”, 5thInternational Conference on Bio-Medical Engineering and Informatics (BMEI 2012), pp.573-576, 2012.
- Zhang Yongjun,” Research and Implementation of the Optimization RS Decoding Algorithms for QR Code Decoding”, IEEE,3rd InternationalConference on System Science, Engineering Design and Manufacturing Informatization, pp.235-238, 2012.
- Max E. VizcarraMelga, AlexandreZaghetto, Bruno Macchiavello, Anderson CA Nascimento, "CQR codes: Colored quick-response codes", IEEEInternational Conference on Consumer Electronics, pp. 321-325, 2012.
|