Keywords
|
| OFDM, PAPR, SPIHT, LDPC, Trigonometrictransforms. |
I.INTRODUCTION
|
| OFDM modulation has been adopted by several wireless multimedia transmission standards, such as Digital Audio Broadcasting(DAB)and Digital Video Broadcasting (DVB-T), because it provides a high degree of immunity to multipath fading and impulsive noise. High spectral efficiency and efficient modulation and demodulation by IFFT/FFT are also advantages of OFDM In the frequency selective retransmission channel, all fading and Inter-Symbol Interference (lSI) result in severe losses of transmitted image quality. OFDM divides frequency-selective channel into several parallel no frequency selective narrow-band channels, and modulates signal into different frequencies. It can significantly improve the channel transmission performance without employing complex equalization schemes. It also has broad application prospect in wireless image and video communications [1, 2]. There are still some challenging issues, which remain unresolved in the design of OFDM systems. One of the major problems is high PAPR of transmitted OFDM signals. Therefore, the OFDM receiver detection efficiency is very sensitive to the nonlinear devices used in its signal processing loop, such as Digital-to-Analog Converter (DAC) and High Power Amplifier (HP A), which may severely impair system performance due to induced spectral regrowth and detection efficiency degradation. There are several developed techniques to reduce the PAPR in OFDM systems [3, 4] such as clipping. [5], companding [6, 7], Partial Transmit Sequence (PTS) [8], Selected Mapping (SLM) [9] and coding [lO]. The clipping technique is the simplest one that can be used in OFDM systems, but it causes additional clipping no which degrades the system performance. An alternative technique to mitigate the PAPR problem is based On signal transformationsThis technique involves a signal transformation prior to amplification, then an inverse transformation at the receiver prior to demodulation. In [11] trigonometric transforms were suggested as alternatives for the FFT to reduce the PAPR. The authors in [11] concluded that OFDM systems with trigonometric transforms provide higher PAPR reduction than the standard FFT based system. However, modified the OFDM symbols before transmission using the PTS. Their results reveal that without PTS, the distribution of PAPR is the same for that conventional one such that the reduction depends on PTS, which makes redundancy in the system. The SPHIT algorithm has been introduced by Said and Pearlman [12]. It is algorithm based on the wavelet transform, and restricts the necessity of random access to the whole image to small sub images. The principle of the SPIRT is partial ordering by magnitude with a set partitioning sorting algorithm, ordered bit plane transmission, and exploitation of self similarity across different scales of an image wavelet transform. The success of this algorithm in compression efficiency and simplicity makes it well known as a benchmark for embedded wavelet image coding. The SPHIT is used for image transmission over the OFDM system in several research works [13, 14] because the SPIRT has a good rate-distortion performance for still images with comparatively low complexity and it is scalable or completely embeddable. To improve the BER performance of the OFDM system, several error correcting codes have been applied to OFDM. LDPC codes have attracted much attention particularly in the field of coding theory. LDPC codes are a class of linear block codes which provide a reliable transmission for coding performance that is very close to the Shannon's limit and can outperform Turbo codes at long block length but with relatively low decoding complexity. LDPC has been adopted as the DVB-S2 standard. A (N, K) LDPC code can be represented by a very sparse parity-check matrix having M rows, N columns and code rate R=KIN, where K=N-M. It was originally invented by Gallager in 1963 [15] and rediscovered by Mackay and Neal recently [16]. The combination of the high spectral efficiency OFDM modulation technique and LDPC coding will be a good candidate for high speed broadband wireless applications. The BER performance of the Low Density Parity Check Coding- Coded Orthogonal Frequency Division Multiplexing system (LDPC-COFDM) is influenced by the sub channels which have deep fad due to frequency selective fading. According to this combination, several algorithms were introduced into LDPC-COFDM system to improve the BER by adaptive bit loading and power allocation of each subcarrier [17], [18]. The paper concentrates on two targets reducing the PAPR of the OFDM signal and improving the quality of the reconstructed images. It considers the trigonometric transforms as a way for reducing the P APR by using the character of the DCT/DST energy focused in the low component. The data of OFDM signal is modulated by IFFT then using DCTIDST, which can reduce the PAPR. Compared with the means of SLM-OFDM and PTS-OFDM, OFDM system modified by DCT/DST maintain the system orthogonal properties, which will not result in additional noise and need not transmit side information. At the same time, the proposed method reduces the PAPR greatly and the system hascharacter of low complexity hardware. |
| Literature review - There are several developed techniques to reduce the PAPR in OFDM systems such as clipping, companding , Partial Transmit Sequence (PTS) , Selected Mapping (SLM) and coding . The clipping technique is the simplest one that can be used in OFDM systems, but it causes additional clipping no which degrades the system performance. An alternative technique to mitigate the PAPR problem is based On signal transformationsThis technique involves a signal transformation prior to amplification, then an inverse transformation at the receiver prior to demodulation. Y. Sun, X. Wang and Liu proposed the paper[13] "A Joint Channel Estimation and Unequal Error Protection Scheme for Image Transmission in Wireless OFDM Systems.Gusmo, R. Dinis and N. Esteves[2] ,proposed the paper " On Frequency Domain Equalization and Diversity Combining for Broadband Wireless Communications" This is concerned with the use of frequency-domain equalization (FDE) and space diversity within block transmission schemes for broadband wireless communications. C. Yuan Yang and M. Kai Ku[18] proposed the paper, "LDPC Coded OFDM Modulation for High Spectral Efficiency Transmission" This paper investigates efficient low-density paritycheck (LDPC) coded orthogonal frequency division multiplexing (OFDM) modulation schemes for fixed wireless application. |
II.SYSTEM MODEL AND ASSUMPTIONS
|
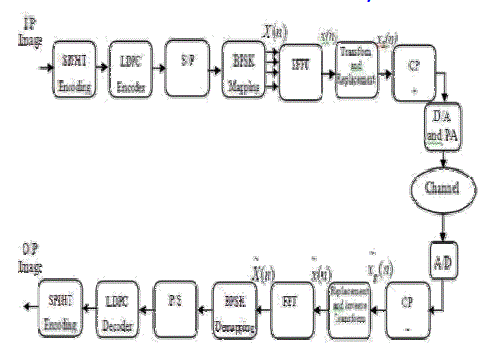
| The block diagram of the proposed LDPC-COFDM system is illustrated in Fig. 2. As will be shown in the next sections, the proposed modifications will be in the transform and replacement block. The SPIRT coder is chosen the source coding technique due to its flexibility of code rate and simplicity of designing optimal system. The SPHIT divides the image stream into several layers according to the importance of progressive image stream. |
| Then the image stream is converted to a binary format. Afterwards the information bits are LDPC encoded at the LDPC encoder. The OFDM considered in this paper utilizes N frequency tones (number of subcarriers) hence the baseband data is first converted into parallel data of N subchannels so that each bit of a codeword is on different subcarrier. The N subcarriers are chosen to be orthogonal, Then, the transmitted data of each parallel subchannel is modulated by Binary phase Shift Keying (BPSK) modulation because it provides high throughput and best performance when combined with the OFDM. Finally, the modulated data are fed into an IFFT circuit, such that the OFDM signal is generated. The resulting OFDM signal can be expressed as follows: |
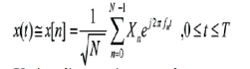 |
| whereXn is a discrete time sample. |
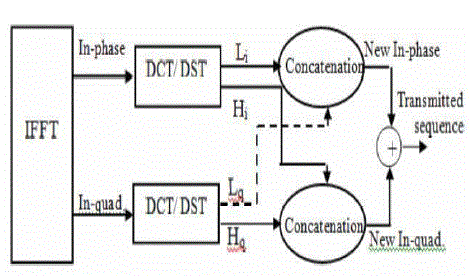
| The output of IFFT is split into two components; in-phase and in-quadrature. Then, either the DCT or the DST is applied to both components, separately. The first half of samples of the in-phase component after the transform (Li) is concatenated with the first half of samples of the in-quadrature component after the transform (Lq) to form the new inphase component. Similarly, the second half of samples of the in-phase component after the transform (Hi) is concatenated with the second half of samples of the in-quadrature component after the transform (Hq) to form the new in-quadrature component. Finally, the new components are added to produce the OFDM signal as shown in Fig. 3. This sequence after this process can be called (xin) with the subscript d referring to the trigonometric transformation process. Each data block is padded with a cyclic prefix (CP) of a length longer than channel impulse response to mitigate the Inter-Block Interference (IBI). The continuous COFDM signal x/.J) is generated at the output of the digital to Analog (D/A) converter. According to [I], the PAPR of transmitted Analog signal can be expressed as follows: |
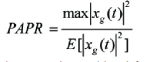 |
| where E[.] is the average power. Generally, the PAPR is considered for a single OFDM symbol, which has a time duration T. This duration comprises a number of samples equal to (Nf +Ng), where Ng is the guard interval length. At the receiver, the guard interval is removed and the time interval [O,T] is evaluated. The replacement and inverse transform are then applied to the received samples. Afterwards, the OFDM sub channel demodulation is implemented by using a (FFT) then the Parallel-to-Serial (P/S) conversion is implemented. This received OFDM symbols are demodulated at the demodulator. The demodulated bits are decoded with each LDPC encoded block and data bits are restored. These data are converted into image format, such that SPIHT decoder can be obtained. |
III.THE SPIHT ALGORITHM
|
| The SPHIT algorithm defines and partitions sets in the wavelet decomposed image using a special data structure called a spatial orientation tree. A spatial orientation tree is a group of wavelet coefficients organized in to a tree rooted in the lowest frequency (coarsest scale) subband with offspring in several generations along the same spatial orientation in the higher frequency subband. Fig.1, shows a spatial orientation tree and the parent children dependency defied by the SPHIT algorithm across subband in the wavelet image. The tree is defied in such a way that each node has either no offspring (the leaves) or four offspring at the same spatial location in the next from subband level. The pixels in the lowest frequency subband-tree roots are grouped into blocks of 2x2 adjacent pixels, and in each block one of them; marked by star as shown in Fig. 1; has no descendants. SPIRT describes this collocation with one to four parentchildren relationships, |
| parent = (i,j) |
| children = [(2i,2j),(2i + 1,2j),(2i,2j + 1),(2i + 1,2j + 1)] |
| The SPHIT algorithm consists of three stages: initialization, sorting and refinement. It sorts the wavelet coefficients into three ordered lists: the list of insignificant sets (LIS), the List of Insignificant Pixels (LIP), and the List of Significant Pixels (LSP). At the initialization stage the SPIRT algorithm first defines a start threshold based on the maximum value in the wavelet pyramid, then sets the LSP as an empty list and puts the coordinates of all coefficients in the coarsest level of the wavelet pyramid (Le. the lowest frequency band; LL band) into the LIP and those which have descendants also into the LIS. In the sorting pass, the algorithm first sorts the elements of the LIP and then the sets with roots in the LIS. For each pixel in the LIP it performs a significance test against the current threshold and outputs the test result to the output bit stream. All test results are encoded as either 0 or 1, depending on the test outcome, so that the SPHIT algorithm directly produces a binary bit stream. If a coefficient is significant, its sign is coded and its coordinate is moved to the LSP. During the sorting pass of LIS, the SPHIT encoder carries out the significance test for each set in the LIS and outputs the significance information. If a set is significant, it is partitioned into its offspring and leaves. Sorting and partitioning are carried out until all significant coefficients have been found and stored in theLSP.After the sorting pass for all elements in the LIP and LIS, SPHIT does a refmement pass with the current threshold for all entries in the LSP, except those which have been moved to the LSP during the last sorting pass. Then the current threshold is divided by two and the sorting and refmement stages are continued until a predefined bit-budget is exhausted. Details of SPHIT algorithms are presented in [12].In this scheme, each node with message searches for possible path nodes to copy its message. Hence, possible path nodes of a node are considered. Using NSS, each node having message selects its path nodes to provide a sufficient level of end-to-end latency while examining its transmission effort. Here, it derives the CSS measure to permit CR-Networks nodes to decide which licensed channels should be used. The aim of CSS is to maximize spectrum utilization with minimum interference to primary system. Assume that there are M licensed channels with different bandwidth values and ydenotes the bandwidth of channel c. Each CR-Networks node is also assumed to periodically sense a set of M licensed channels. Midenotes the set including Ids of licensed channels that are periodically sensed by node i. suppose that channel c is periodically sensed by node i in each slot and channel c is idle during the time interval xcalled channel idle duration. Here, it use the product of channel bandwidth yand the channel idle duration x, tc= xy, as a metric to examine the channel idleness. Furthermore, failures in the sensing of primary users are assumed to cause the collisions among the transmissions of primary users and CR-Networks nodes. |
IV. RESULT AND DISCUSSION
|
| In this section, simulation experiments are carried out to study the transmission of SPIHT coded images on LDPC COFDM modified by Trigonometric transforms over AWGN channel. The parameters used in the simulation are: the number of subcarriers of a LDPC coded OFDM system ( N) is considered to be 256, Cyclic Prefix is 64, Rate of the SPIHT (r) = 0 to l. LDPC code of R = 1;2 is employed with sum-product decoding, where R denotes the code rate and a (512, 1024) parity check matrix is used. The maximum number of iterations in sum-product decoding is set to 10. The input image is 8 bits per pixel, grayscale test image, 'Building' from MATLAB toolbox is utilized in the simulation has a resolution 256x256 pixels. The fidelity of it was measured by the Peak Signal-to-Noise Ratio, PSNR, which usually expressed in terms of the logarithmic scale. MSE is the mean squared error between the original and the reconstructed image, and Peak is the maximum possible magnitude for a pixel inside the image. The peak value is 255 for an 8 bits/pixel of original image. To verify the effectiveness of the proposed method; adding Trigonometric transforms to the OFDM system to reduce the P APR, the analysis is divided into two methods one with DCT and another with DST and compare them with COFDM and set SPIHT coder as source coding. The three transmission schemes were designed |
| as |
| follows: |
| Scheme I : The system which consists of coded OFDMïÃâ¬Ã |
| Scheme II : The system I with the DCT transforms forthe transmitted signal |
| Scheme III: The system I with the DST transform forthe transmitted signal. |
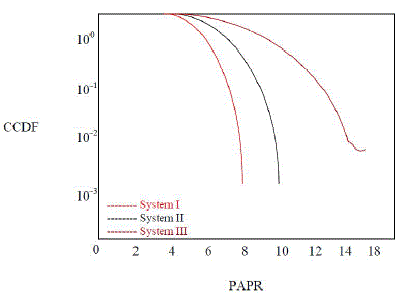
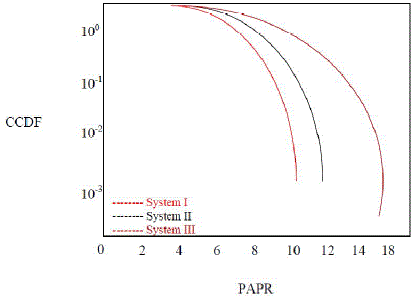
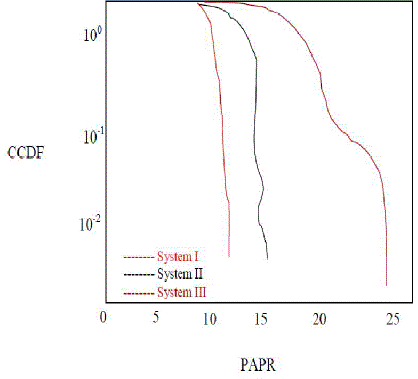
| Simulation were carried out respectively according to the above three schemes. Firstly, we present the simulation of the complementary cumulative distribution function (CCDF) curves for the proposed SPIHT LDPC COFDM with Trigonometric transforms. The CCDF is a useful statistical indication about the signal power distribution. It is defined as the probability that the signal is at or higher thana given amplitude PAPR• Fig. 3 (a, b) shows the CCDFs of the PAPR for the three proposed schemes at different SPIHT rates: 0.5 and 1 respectively. |
| Clearly, the PAPR performance of the proposed systems II and III outperforms the system I without each other. The figure reveals that system with the DST has a better reduction in the PAPR than that with the DCT nearly up to 0.25dB (Fig. 3(b)). It is also noted that the PAPR can be achieved by increasing the value of SPIHT rate as the data increased and the statistical distribution is clearer.On the other side, the effect of the SPIHT compression ratios on the PSNR of the received image results in the three schemes and compare with the OFDM system without LDPC. |
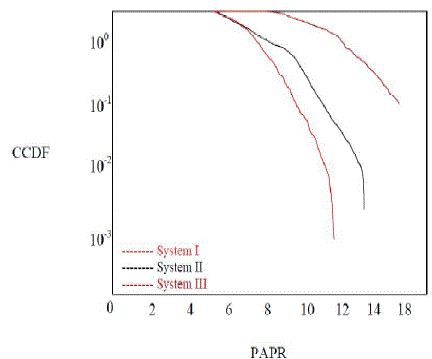
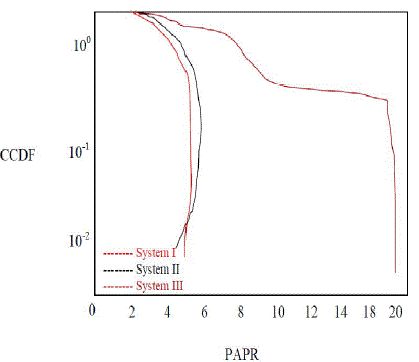
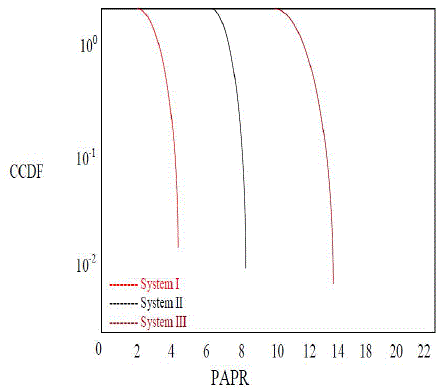
| For the lower SNR values (5dB), the PSNR performance deteriorates for all schemes except that with the DST however at higher SNR values (l0dB or greater) all the schemes have the ideal performancewhich is equal to the output of SPHIT Compression. It can be noticed form this figure, for system III at low SNR and all systems at higher SNR, as the SPHIT rate increases the PSNR also increases. This is due to the fact of injecting more information about the image to the receiver and thus it will have more capability to reproduce a better reconstructed image. Finally, the impact of the number of subcarriers on the performance of the three schemes is studied and shown in Fig.4 at lower SPIRT rate r = 0.2 to save the bandwidth on the channel. |
| It is clear that, the Scheme III provides a significant PAPR reduction, especially for a large number of subcarriers.and Fig.5 shows the output and input image in transmitter and receiver side , and also Table 1. shows Describing the Different PAPR values Using 256*256 grayscale image . |
V.CONCLUSION
|
| In this paper, an efficient LDPC coded OFDM system with trigonometric transforms supporting image transmission using SPIHT compression technique is presented and studied. The effectiveness of the proposed system is investigated through simulations over AWGN channel. It is found that the proposed system must be designed carefully in order to achieve a reduction in the PAPR without degrading the PSNR performance. For LDPC COFDM with rate (R=O.5) and rate of SPHIT rate (r = 1) the OFDM signal can be reduced by nearly 7dB or 7.25dB by adding the DCT or DST respectively. We also showed the PSNR for the received image at different rates. This work shows the performance of the system model using 256x256 grayscale images. |
| |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3a |
Figure 3b |
Figure 4a |
 |
 |
 |
 |
| Figure 4b |
Figure 4c |
Figure 4d |
Figure 5 |
|
| |
References
|
- H. Schulze and C. Lauders,” Theory and Application of OFDM and CDMA Wideband Wireless Communication”. John Wiley,pp.94-101,2005.
- Gismo, R. Denis and N. Estevez, "On Frequency Domain Equalization and Diversity Combining for Broadband Wireless Communications"IEEE Common. Lett., Vol. 51, No. 7, July 2003.
- T. Jiang and Y. Wu, "An Overview: Peak-to-Average Power Ratio Reduction Techniques for OFDM Signals",IEEE Transactions on Broadcasting, Vol. 54, No. 2, pp. 257-268, Jun. 2008.
- F.S. AI-Kamali, M. I. Dessouky, B.M. Sallam, F. Shawki and F. E. Abd EI-Samie, "Transceiver Scheme For Single-Carrier Frequency DivisionMultiple Access Implementing the Wavelet Transform and PeakTo-Average-Power Ratio Reduction Methods" lET Communications, Vol. 4, No.1, pp. 69-79, 2010.
- J. Kim and Y. Shin, "An Effective Clipped Companding Scheme for PAPR Reduction of OFDM Signals", Proceedings of the IEEE ICC'08,pp.668-672, 2008.
- T. Jiang, W. Yao, P. Guo, Y. Song and D. Qu, "Two Novel Nonlinear Companding Schemes With Iterative Receiver to Reduce PAPR in Multi-Carrier Modulation Systems", IEEE Transactions on Broadcasting, Vol. 51, No. 2, pp. 268 - 273, Jun. 2006
- F. S. AI-Kamali, M. I. Dessouky, B. M. Sallam, F. Shawki and F. E. Abd EI-Samie, "Performance Enhancement of SC-FDMA Systems Using aCompanding Technique", Ann. Telecommun. , Vol. 65, No. 5-6, pp. 293-300, 2010.
- L. Guan, T. Jiang, D. Qu and Y. Zhou, "Joint Channel Estimation and PTS to Reduce Peak-to-AveragePower Radio in OFDM Systems withoutSide Information", IEEE Signal Processing Letters, Vol. 17, No. 10, pp. 883-886, October 2010.
- E. S. Hassan, S. E. EI-Khamy, M. I. Dessouky, S. A. EI-Dolil and F. E. Abd EI-Samie, "A Simple Selective Mapping Algorithm For The PeakTo Average Power Ratio In Space Time Block Coded MIMO-OFDM Systems" Proceedings of the International Conference on HighPerformance Computing, Networking and Communication Systems
- T. Jiang and G. Zhu , "Complement Block Coding for Reduction in Peak-to-Average Power Ratio of OFDM Signals," IEEE CommunicationsMagazine, vol. 43, no.9, pp. S17 - S22, Sept. 2005.
- A. Rushdi and J. Tuqan, "Peak reduction in Trigonometric Based OFDM System", Proceedings in ACSSC.2007, pp. 1747 - 1751, 2007.
- Said and W.A. Pearhnan, "A New, Fast and Efficient Image Codec Based on Set Partitioning In Hierarchical Trees", IEEE Trans. Circuits Syst.Video Technol., Vo1.6, pp. 243-250, 1996.
- Y. Sun, X. Wang and Liu, K.J.R, "A Joint Channel Estimation and Unequal Error Protection Scheme for Image Transmission in WirelessOFDM Systems", Multimedia Signal Processing, IEEE, pp. 380 - 383,
|