ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| M.A.Gopalan1 , G.Sumathi2 , S.Vidhyalakshmi3 Professor, PG and Research, Department of Mathematics, Shrimati Indira Gandhi, College,Trichy-620002,Tamilnadu,India1 Lecturer, PG and Research, Department of Mathematics, Shrimati Indira Gandhi College , Trichy-620002,Tamilnadu,India2 Professor, PG and Research, Department of Mathematics , Shrimati Indira Gandhi College, Trichy-620002,Tamilnadu,India3 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The non-homogeneous quintic equation with three unknowns represented by the diophantine equation 2 2 2 5 x y xy x y 1 (k 3) z n       is analyzed for its patterns of non-zero distinct integral solutions and three different methods of integral solutions are illustrated. Various interesting relations between the solutions and special numbers, namely, polygonal numbers, Jacobsthal numbers, Jacobsthal-Lucas number,Pronic numbers, Stella octangular numbers, Octahedral numbers, Centered Polygonal numbers, Centered Pentagonal Pyramidal numbers, Centered Hexagonal Pyramidal numbers, Generalized Fibonacci and Lucas sequences, Fourth Dimensional Figurate numbers and Fifth Dimensional Figurate numbers are exhibited.
Keywords |
||||||||||
| Integral solutions, Generalized Fibonacci and Lucas sequences, Quintic non-homogeneous equation with three unknowns | ||||||||||
| M.Sc 2000 mathematics subject classification: 11D25 | ||||||||||
NOTATIONS |
||||||||||
| tm,n : Polygonal number of rank n with size m | ||||||||||
| Prn : Pronic number of rank n | ||||||||||
| Son : Stella octangular number of rank n | ||||||||||
| jn : Jacobsthal lucas number of rank n | ||||||||||
| J n : Jacobsthal number of rank n | ||||||||||
| GFn : Generalized Fibonacci sequence number of rank n | ||||||||||
| GLn : Generalized Lucas sequence number of rank n | ||||||||||
| Ctm,n : Centered Polygonal number of rank n with size m | ||||||||||
| Cf3,n,5 : Centered Pentagonal Pyramidal number of rank n | ||||||||||
| Cf3,n,6 : Centered Hexogonal Pyramidal number of rank n | ||||||||||
| f4,n,3 : Fourth Dimensional Figurate Traingular number of rank n | ||||||||||
| f4,n,4 : Fourth Dimensional Figurate Square number of rank n | ||||||||||
| f4,n,6 : Fourth Dimensional Figurate Hexogonal number of rank n | ||||||||||
| f5,n,3 : Fifth Dimensional Figurate Traingular number of rank n | ||||||||||
| f5,n,7 : Fifth Dimensional Figurate Heptagonal number of rank n | ||||||||||
INTRODUCTION |
||||||||||
| The theory of diophantine equations offers a rich variety of fascinating problems. In particular,quintic equations, homogeneous and non-homogeneous have aroused the interest of numerous mathematicians since antiquity[1-3].For illustration, one may refer [4-5] for quintic equation with three unknowns and [6-8] for quintic equation with five unknowns. This communication concerns with an interesting non-homogeneous ternary quintic equation with three unknowns represented by | ||||||||||
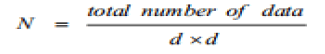 |
||||||||||
| for determining its infinitely many non-zero integral points. Three different methods are illustrated. In method 1, the solutions are obtained through the method of factorization. In method 2, the binomial expansion is introduced to obtain the integral solutions. In method 3, the integral solutions are expressed in terms of Generalized Fibonacci and Lucas sequences along with a few properties in terms of the above integer sequences Also, a few interesting relations among the solutions are presented. | ||||||||||
II.METHOD OF ANALYSIS |
||||||||||
| The Diophantine equation representing a non-homogeneous quintic equation with three unknowns is | ||||||||||
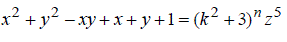 (1) (1) |
||||||||||
| Introducing the linear transformations | ||||||||||
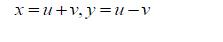 (2) (2) |
||||||||||
| in (1), it leads to | ||||||||||
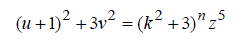 (3) (3) |
||||||||||
| The above equation (3) is solved through three different methods and thus, one obtains three distinct sets of solutions to (1). | ||||||||||
| A. Method:1 | ||||||||||
Let 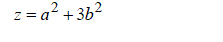 (4) (4) |
||||||||||
| Substituting (4) in (3) and using the method of factorization,define | ||||||||||
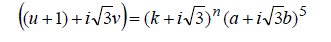 (5) (5) |
||||||||||
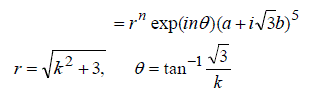 (6) (6) |
||||||||||
| Equating real and imaginary parts in (5) we get | ||||||||||
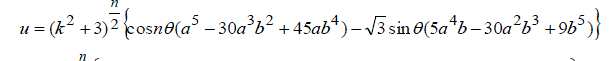 |
||||||||||
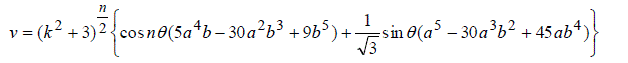 |
||||||||||
| Substituting the values of u and v in (2), the corresponding values of x, y, z are represented by | ||||||||||
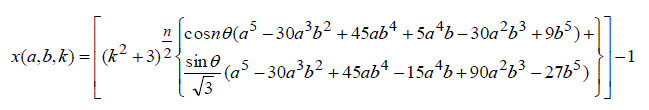 |
||||||||||
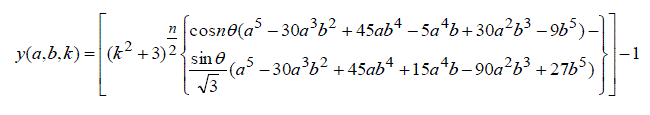 |
||||||||||
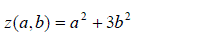 |
||||||||||
| A few numerical examples are given below: | ||||||||||
| Table: Numerical Examples: | ||||||||||
 |
||||||||||
| B. Method 2: | ||||||||||
Using the binomial expansion of 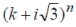 in (5) and equating real and imaginary parts, we have in (5) and equating real and imaginary parts, we have |
||||||||||
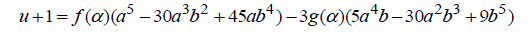 |
||||||||||
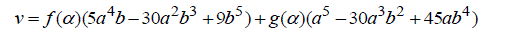 |
||||||||||
| Where | ||||||||||
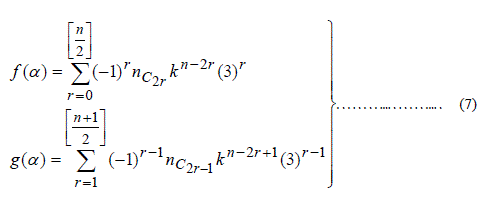 |
||||||||||
| In view of (2) and (7) the corresponding integer solution to (1) is obtained as | ||||||||||
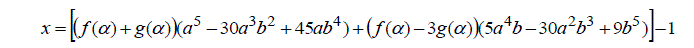 |
||||||||||
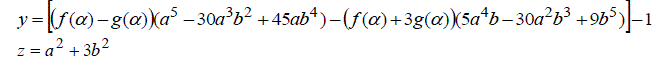 |
||||||||||
| C. Method 3: | ||||||||||
| Taking n = 0 and u +1=U in (3), we have, | ||||||||||
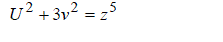 (8) (8) |
||||||||||
| Substituting (4) in (8), we get | ||||||||||
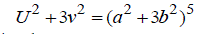 (9) (9) |
||||||||||
| whose solution is given by | ||||||||||
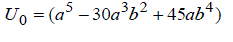 |
||||||||||
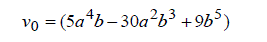 |
||||||||||
| Again taking n =1 in (3), we have | ||||||||||
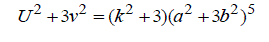 (10) (10) |
||||||||||
| whose solution is represented by | ||||||||||
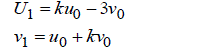 |
||||||||||
| The general form of integral solutions to (1) is given by | ||||||||||
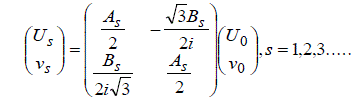 |
||||||||||
| Where | ||||||||||
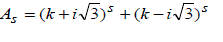 |
||||||||||
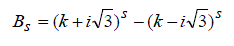 |
||||||||||
| Thus, in view of (2), the following of integers xs , ys interms of Generalized Lucas and fiboanacci sequence satisfy (1) are as follows: | ||||||||||
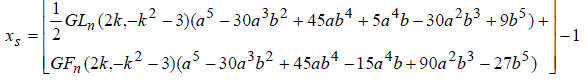 |
||||||||||
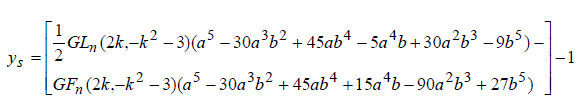 |
||||||||||
| The above values of xs , ys satisfy the following recurrence relations respectively | ||||||||||
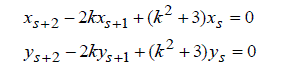 |
||||||||||
| Properties | ||||||||||
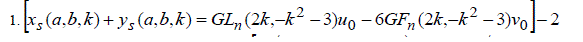 |
||||||||||
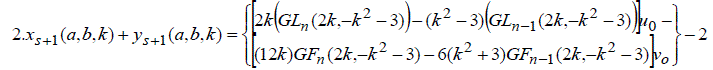 |
||||||||||
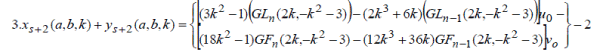 |
||||||||||
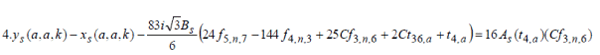 |
||||||||||
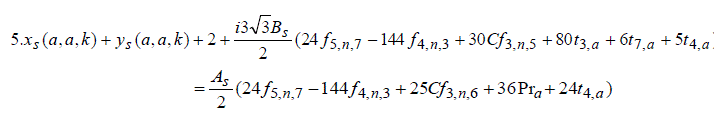 |
||||||||||
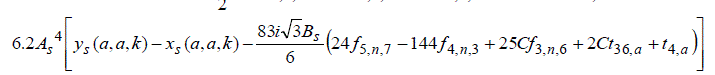 |
||||||||||
| is a quintic integer. | ||||||||||
| 7.Each of the following is a nasty number. | ||||||||||
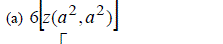 |
||||||||||
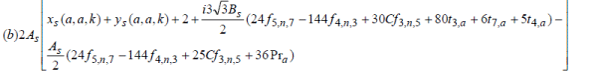 |
||||||||||
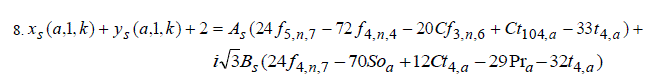 |
||||||||||
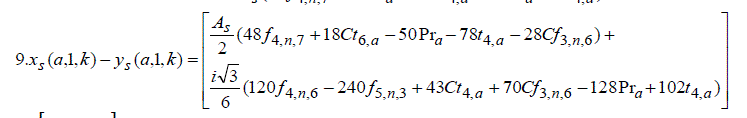 |
||||||||||
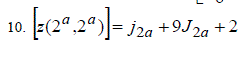 |
||||||||||
III. CONCLUSION |
||||||||||
| To conclude, one may search for other pattern of solutions and their corresponding properties. | ||||||||||
Tables at a glance |
||||||||||
|
||||||||||
Figures at a glance |
||||||||||
|
||||||||||
References |
||||||||||
|