International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Intelligent Adaptive Filtering For Noise Cancellation

Vartika Anand1, Shalini Shah2, Sunil Kumar3
  1. Student of M.Tech., Department of ECE, Amity School of Engineering & Technology, Noida, India
  2. Assistant Professor, Department of ECE, Amity School of Engineering & Technology, Noida, India
  3. Assistant Professor, Department of ECE, Amity School of Engineering & Technology, Noida, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In current scenario of modern technology, we are facing a necessity of noise removal in signal processing. Various approaches are used for the same. This paper describes an intelligent adaptive filtering for noise cancellation. Here ANFIS method is being used for removal of noise from audio speech signals. An audio signal contaminated with noise is taken and inspected with eight types of membership functions: bell MF, triangle MF, Gaussian MF, two-sided MF, pi-shaped MF, product of two sigmoid MF, difference of two sigmoid MF and trapezoidal MF. Finally using ANFIS, the original audio speech signal is restored. The major advantage of this system is its ease of implementation and faster convergence rate.

 

Keywords
Filtering, ANFIS, Noise Cancellation, Gaussian Noise, Bell MF.

INTRODUCTION
Filtering is a signal processing operation whose objective is to process a signal in order to manipulate the information contained in the signal. A digital filter is the one that processes discrete-time signals represented in digital format. For time-invariant filters the internal parameters and the structure of the filter are fixed, and if the filter is linear the output signal is a linear function of the input signal. Once prescribed specifications are given, the design of timeinvariant linear filters entails three basic steps, namely: the approximation of the specifications by a rational transfer function, the choice of an appropriate structure defining the algorithm, and the choice of the form of implementation for the algorithm [1].
An adaptive filter is required when either the fixed specifications are unknown or the specifications cannot be satisfied by time-invariant filters. The adaptive filters are time-varying since their parameters are continually changing in order to meet a performance requirement. Adaptive filters are considered nonlinear systems; therefore their behaviour analysis is more complicated than for fixed filters.
Soft computing is a new approach to construct intelligent systems. The complex real world problems require intelligent systems that combine knowledge, techniques and methodologies from various sources. Neuro fuzzy is the combination of neural network and furzy logic. Neural networks recognize patterns and adapt themselves to cope with changing environments. Fuzzy inference systems incorporate human knowledge and perform inferencing and decision making. Noise is an unwanted energy, which interferes with the desired signal. It can be suppressed with adaptive filters using signal processing. But if the noise frequency is same as the original signal then sometimes it also eliminates the desired signal. Therefore, noise cancellation is used which will not affect the desired signal. The basic principle of noise cancellation using neuro fuzzy is to filter out an interference component by identifying the nonlinear model between a measurable noise source and the corresponding immeasurable interference. The matlab command called 'ANFIS' (Adaptive Neuro Fuzzy Inference System) is used to demonstrate how noise cancellation can be applied as interference canceling in a signal [2].

RELATED WORK
A considerable research effort has been devoted to adaptive filtering for noise cancellation in the last few years. Many new researches have been proposed and various simulators are being used for simulation and performance analysis.
In this paper a simple neural network called Adaline as adaptive filter. Experiment was based on engine noise cancellation in cars. It shows that SNR improves after passing the noise cancellation system. In the first experiment with low engine noise improvement was 7.12 dB, and in the second experiment with high engine noise we achieved an 8.46 dB improvement. Lower improvement in the third test can be explained by wind and road noise in a driving car [3].
In this paper presents an adaptive noise cancellation algorithm based fuzzy and neural network. The major advantage of the proposed system is its ease of implementation and fast convergence. The propose algorithm is applied to noise canceling problem of long distance communication channel. The simulation result showed that the proposed model is effectiveness [4].
This paper concentrates upon the analysis of adaptive noise canceller using Recursive Least Square (RLS), Fast Transversal Recursive Least Square (FTRLS) and Gradient Adaptive Lattice (GAL) algorithms. The performance analysis of the algorithms is done based on convergence behaviour, convergence time, correlation coefficients and signal to noise ratio. After comparing all the simulated results we observed that GAL performs the best in noise cancellation in terms of Correlation Coefficient, SNR and Convergence Time. RLS, FTRLS and GAL were never evaluated and compared before on their performance in noise cancellation in terms of the criteria considered here [5].
A new kind of nonlinear adaptive filter, the adaptive neural fuzzy filter (ANFF), based upon a neural network’s learning ability and fuzzy if-then rule structure, is proposed in this paper. The ANFF is inherently a feed forward multilayered connectionist network which can learn by itself according to numerical training data or expert knowledge represented by fuzzy if-then rules. Then adaptation here includes the construction of fuzzy if-then rules (structure learning), and the tuning of the free parameters of membership functions (parameter learning). In this new ANFF, we also made the learning and fuzziness parameters adaptive. In parameter learning phase, a back propagation-like adaptation algorithm is developed to minimize the output error. There are no hidden nodes initially, and both the structure earning and parameter learning are performed concurrently as the adaptation proceeds [6].
In this paper an adaptive noise canceller will be presented and some useful observations will be done over the audio signals. The adaptive noise canceller is very efficient and useful system in many applications with sound video etc [7].
It showed a cooperative performance study between the time-varying LMS (TV-LMS) and other two main adaptive approaches: The Least Mean Square (LMS) algorithm and the Recursive Least Square (RLS) algorithm. Their study disclosed the algorithm execution time, the minimum Mean Square Error (MSE) and required filter order [8].
This paper uses averaging analysis to study the mean-square performance of adaptive filters, not only in terms of stability conditions but also in terms of expressions for the mean-square error and the mean-square deviation of the filter, as well as in terms of the transient performance of the corresponding partially averaged systems [9].
This paper presented a nice tradeoff between convergence properties and computational complexity and showed that the convergence property of fast affine projection (FAP) adaptive filtering algorithm is superior to that of usual LMS, NLMS, and RLS algorithm [10].
This paper investigates the performance of LMS and NLMS adaptive algorithms when implemented on Texas Instruments (TI) TMS320C6713 DSP hardware [8]-[10] and tested for two types of signals; sinusoidal tone signal and ECG signal. The obtained results from DSP kit are analyzed with the help of Digital Storage Oscilloscope (DSO) and shows considerable improvement in SNR level of a filtered signal [11].
Bernard Widrow et.al. developed a model for noise cancelation with the help of adaptive filter and employed for variety of practical applications like the cancelling of various forms of periodic interference in electrocardiography, the cancelling of periodic interference in speech signals, and the cancelling of broad-band interference in the side-lobes of an antenna array [12].

ADAPTIVE FILTERING
Digital signal processing systems are attractive due to their low cost, reliability, accuracy, small physical sizes, and flexibility. One such digital signal processing system is called filter. Filtering is a signal processing operation whose objective is to process a signal in order to manipulate the information contained in the signal. For time-invariant filters the internal parameters and the structure of the filter are fixed, and if the filter is linear the output signal is a linear function of the input signal. If models are available for the signal and noise, it is possible to design a filter to enhance the signal relative to the noise. Many kinds of non-adaptive filters have been proposed. These include stack filters which are defined based on threshold decomposition and Boolean operations, and Volterra filters which are linear combinations of order stochastics. When the signal and noise models are not completely specified, it seems appropriate models could be estimated by analyzing the actual data. Especially, when the models are ill-defined or are time-varying. This leads to adaptive filters [1] [13].
An adaptive filter is required when either the fixed specifications are unknown or the specifications cannot be satisfied by time-invariant filters. An adaptive filter is a nonlinear filter since its characteristics are dependent on the input signal and consequently the homogeneity and additivity conditions are not satisfied. However, if we freeze the filter parameters at a given instant of time, most adaptive filters are linear in the sense that their output signals are linear functions of their input signals. The adaptive linear filter has achieved a large amount of success in many situations. The adaptive filters are time-varying since their parameters are continually changing in order to meet a performance requirement.
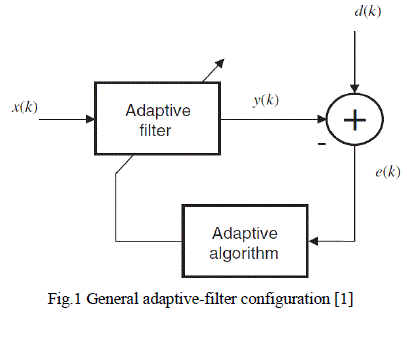
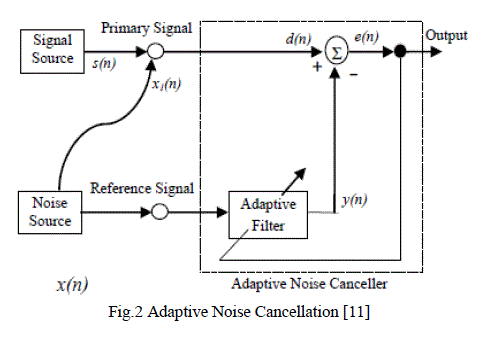
The general set up of an adaptive-filtering environment is illustrated in Fig1. where k is the iteration number, x(k) denotes the input signal, y(k) is the adaptive-filter output signal, and d(k) defines the desired signal. The error signal e(k) is calculated as d(k) − y(k). The error signal is then used to form a performance (or objective) function that is required by the adaptation algorithm in order to determine the appropriate updating of the filter coefficients. The minimization of the objective function implies that the adaptive-filter output signal is matching the desired signal in some sense.
The complete specification of an adaptive system, as shown in Fig.1, consists of three items:
A. Application
The type of application is defined by the choice of the signals acquired from the environment to be the input and desired-output signals. The number of different applications in which adaptive techniques are being successfully used has increased enormously during the last two decades. Some examples are echo cancellation, equalization of dispersive channels, system identification, signal enhancement, adaptive beam-forming, noise cancelling, and control.
B Adaptive-Filter Structure
The adaptive filter can be implemented in a number of different structures or realizations. The choice of the structure can influence the computational complexity (amount of arithmetic operations per iteration) of the process and also the necessary number of iterations to achieve a desired performance level. Basically, there are two major classes of adaptive digital filter realizations, distinguished by the form of the impulse response, namely the finite-duration impulse response (FIR) filter and the infinite-duration impulse response (IIR) filters. FIR filters are usually implemented with non-recursive structures, whereas IIR filters utilize recursive realizations.
1) Adaptive FIR filter realizations: The most widely used adaptive FIR filter structure is the transversal filter, also called tapped delay line, that implements an all-zero transfer function with a canonic direct form realization without feedback. For this realization, the output signal y (k) is a linear combination of the filter coefficients, that yields a quadratic mean-square error (MSE = E[|e(k)|2]) function with a unique optimal solution. Other alternative adaptive FIR realizations are also used in order to obtain improvements as compared to the transversal filter structure, in terms of computational complexity, speed of convergence, and finite word length properties.
2) Adaptive IIR filter realizations: The most widely used realization of adaptive IIR filters is the canonic direct form realization, due to its simple implementation and analysis. However, there are some inherent problems related to recursive adaptive filters which are structure dependent, such as pole-stability monitoring requirement and slow speed of convergence. To address these problems, different realizations were proposed attempting to overcome the limitations of the direct form structure. Among these alternative structures, the cascade, the lattice, and the parallel realizations are considered because of their unique features [1].
C. Algorithm
The algorithm is the procedure used to adjust the adaptive filter coefficients in order to minimize a prescribed criterion. The algorithm is determined by defining the search method (or minimization algorithm), the objective function, and the error signal nature. The choice of the algorithm determines several crucial aspects of the overall adaptive process, such as existence of sub-optimal solutions, biased optimal solution, and computational complexity.

ADAPTIVE ALGORITHMS
Adaptive algorithms have been extensively studied in the past few decades and have been widely used in many arenas including biomedical, image and speed processing, communication signal processing and many other Adaptive algorithms have been extensively studied in the past few decades and have been widely used in many arenas including biomedical, image and speed processing, communication signal processing and many other
A. The Adaptive LMS Algorithm
The LMS algorithm [12] is a stochastic gradient-based algorithm as it utilizes the gradient vector of the filter tap weights to converge on the optimal wiener solution. With each iteration of the LMS algorithm, the filter tap weights of the adaptive filter are updated according to the following formula:
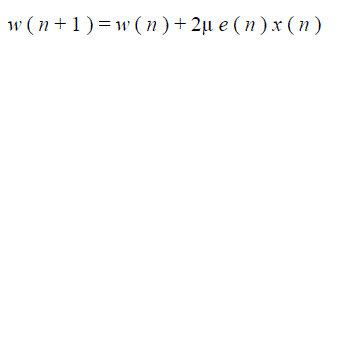image
where, x(n) is the input vector of time delayed input values, w(n) represents the coefficients of the adaptive FIR filter tap weight vector at time n and μ is known as the step size. Selection of a suitable value for μ is imperative to the performance of the LMS algorithm, if the value is too small, the time adaptive filter takes to converge on the optimal solution will be too long; if μ is too large the adaptive filter becomes unstable and its output diverges. Fig.2 represents a model for Adaptive Noise Cancellation.
B. Normalized LMS Algorithm
In the standard LMS algorithm, when the convergence factor μ is large, the algorithm experiences a gradient noise amplification problem. In order to solve this difficulty, we can use the NLMS (Normalized Least Mean Square) algorithm. The correction applied to the weight vector w(n) at iteration n+1 is “normalized” with respect to the squared Euclidian norm of the input vector x(n) at iteration n[1][15].
We may view the NLMS algorithm as a time-varying step-size algorithm, calculating the convergence factor μ as in Eq.2
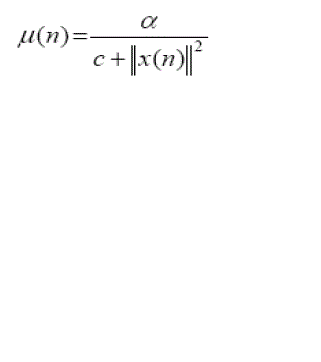image
where α is the NLMS adaption constant, which optimize the convergence rate of the algorithm and should satisfy the condition 0<α<2, and c is the constant term for normalization, which is always less than 1. The filter weights using NLMS algorithm are updated by the Eq. (3).
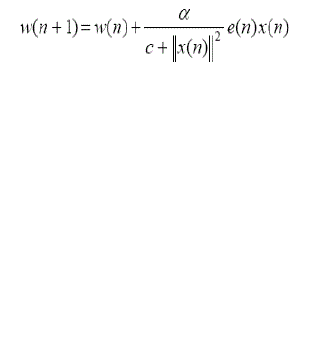image
C. RLS Algorithm
Compared to the LMS algorithm, the RLS algorithm has the advantage of fast convergence but this comes at the cost of increasing the complexity. Hence, the RLS algorithm requires longer computation time as well as a higher sensitivity to numerical instability [8] [14] [16].

SOFT COMPUTING TECHNIQUES FOR NOISE CANCELLATION
Fuzzy logic was introduced by Zadeh in 1965 to represent and manipulate data and information in which there are various forms of uncertainty. Fuzzy logic is a logical system, which is an extension of multi-valued logic. It is almost synonymous with the theory of fuzzy sets, a theory that relates to classes of objects with blunt boundaries in which membership is a matter of degree [2]. ANFIS is a class of adaptive network, which are functionally equivalent to Fuzzy Inference Systems. This architecture was proposed by Jang [9] to give fuzzy systems adaptive capabilities. It uses a hybrid- learning algorithm to identify the membership function parameters of single-output, Sugeno type fuzzy inference systems (FIS). A combination of least-squares and back propagation gradient descent methods are used for training FIS membership function parameters to model a given set of input/output data. The hybrid learning algorithm which combines gradient descent and the least-squares method are briefly discussed below.
A. Artificial Neutral Network
Neural networks are composed of simple elements operating in parallel. The network function is determined largely by the connections between elements. Neural network can be trained to perform a particular function by adjusting the value of the connections (weights) between elements. Artificial Neural Network has preserved three basic characteristics. Neural network learns from experience; generalize from learned responses, and abstract essential pattern from inputs. Neural networks have been trained to perform complex functions in various fields of application including pattern recognition, identification, classification, speech, vision and control systems [2].
ANNs are mathematical modeling tools which are particularly useful for predicting and forecasting in complex settings. The ANN accomplishes this through a large number of highly interconnected processing elements (neurons), working in unison to solve specific problems. Each neuron is connected to some of its neighbors with varying coefficients or weights which represent the relative influence of the different neuron inputs on other neurons [17].
B. Basic concepts in fuzzy logic
There are two basic concepts in fuzzy logic. They are linguistic variable and fuzzy if-then rule or fuzzy rule. There are two basic concepts in fuzzy logic. They are:
1) Linguistic variable: It is a variable whose values are words rather than numbers. Its use is closer to the tolerance for imprecision and thereby lowers the cost of solution. It encapsulates the properties of approximate or imprecise concepts in a systematic and computationally useful way. It also reduces the apparent complexity of describing a system.
2) Fuzzy IF- THEN rule: IF -THEN rule statements are used to formulate the conditional statements that comprise fuzzy logic. A single IF - THEN rule assumes the form
If x is A then y is B
where A and B are linguistic values defined by fuzzy sets on the ranges (universe of discourse) X and Y, respectively.
The IF part of the rule "x is A" is called the antecedent or premise, while the THEN part of the rule "y is B" is called the consequent or conclusion [1][19].
C. Fuzzy inference systems
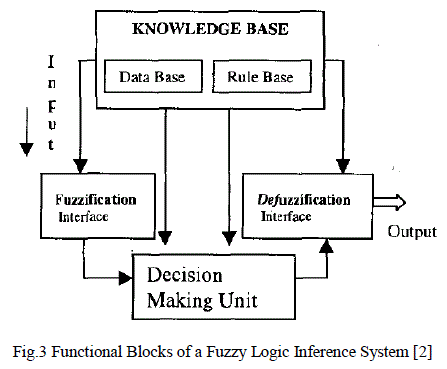
Fuzzy inference (Fig.3) is the process of formulating the mapping from a given input to an output using fuzzy logic. The mapping then provides a basis from which decisions can be made, or patterns discerned an input value to its appropriate membership value [2].
There are two types of FIS:
1. Mamdani-type,
2. Sugeno-type.
Both can be implemented in fuzzy logic toolbox. These two types differ in the way output's are determined. Mamdani-type inference expects the output membership functions to be fuzzy sets. It needs defuzzification. A firstorder Sugeno fuzzy model has a crisp output, the overall output is obtained via weighted average, thus avoiding the time consuming process of defuzzification required in a Mamdani model.

D. Adaptive Neuro-Fuzzy Inference System
The Adaptive Neuro-Fuzzy Inference System, first introduced by Jang, is a universal approximator and as such is able to approximate any real continuous function on a compact set to any degree of accuracy. Thus, in estimating parameters where the given data are such that the system associates measurable system variables with an internal system parameter, functional mapping can be constructed by ANFIS to approximate the process of estimation of the internal system parameter. ANFIS is a neuro-fuzzy system that combines the learning capabilities of neural networks, with the functionality of fuzzy inference systems. An adaptive network is a feed-forward multilayer Artificial Neural Network (ANN) with; partially or completely, adaptive nodes in which the outputs are predicated on the parameters of the adaptive nodes and the adjustment of parameters due to error term is specified by the learning rules[17][18].
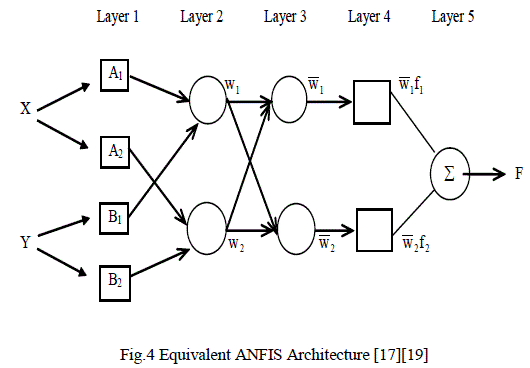
1) ANFIS Architecture: Assume that the fuzzy inference system under consideration has two inputs x and y and one output z. For a first-order Takagi-Sugeno fuzzy model, a common rule set with two fuzzy if-then rules is the following:
 Rule 1: If x is A1 and y is B1, then f1=p1x+q1y+r1;
 Rule 2: If x is A2 and y is B2, then f2=p2x+q2y+r2;
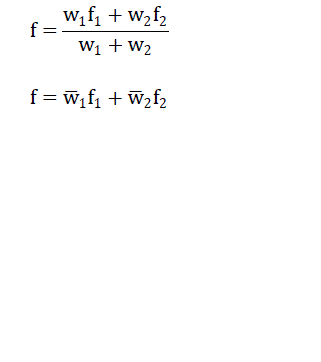image
The equivalent ANFIS architecture is as shown in Fig.4, using a Sugeno fuzzy model where nodes of the same layer have similar functions.
The output of the ith node in layer l is denoted Ol , i
Layer 1 Every node i in this layer is an adaptive node with a node function
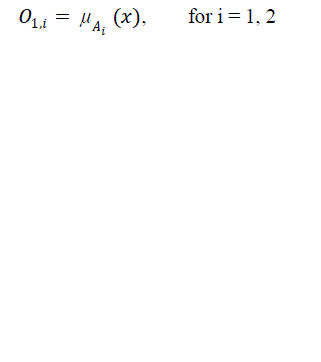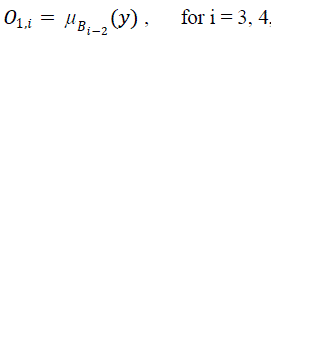image
image
where x (or y) is the input to node i and Ai (or Bi-2) is a linguistic label (such as "small" or "large") associated with this node. In other words, O1,i is the membership grade of a fuzzy set A ( =A1 , A2 , B1 or B2 ) and it specifies the degree to which the given input x (or y) satisfies the quantifier A.
Layer 2 Every node in this layer is a fixed node labeled Π, whose output is the product of all the incoming signals:
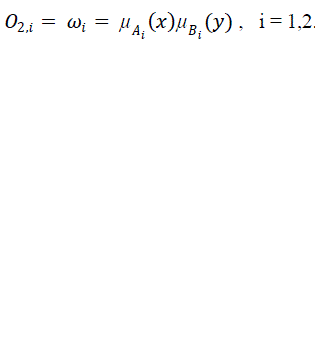image
Each node output represents the firing strength of a rule. In general, any other T-norm operators that perform fuzzy AND can be used as the node function in this layer.
Layer 3 Every node in this layer is a fixed node labeled N. The ith node calculates the ratio of the ith rule's firing strength to the sum of all rules' firing strengths:
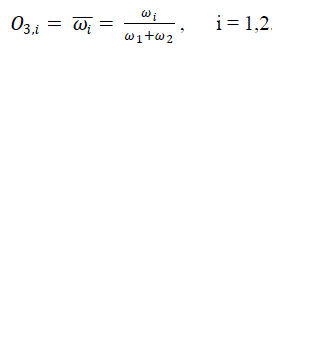image
For convenience, outputs of this layer are called normalized firing strengths.
Layer 4 Every node i in this layer is an adaptive node with a node function:
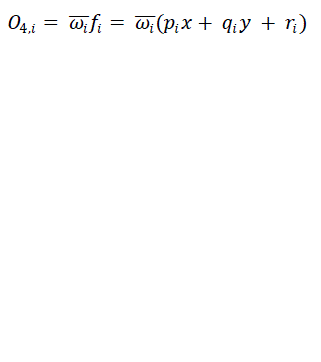image
where anfis is a normalized firing strength from layer 3 and {pi, qi, ri} is the parameter set of this node. Parameters in this layer are referred to as consequent parameters.
Layer 5 The single node in this layer is a fixed node labeled, which computes the overall output as the summation of all incoming signals:
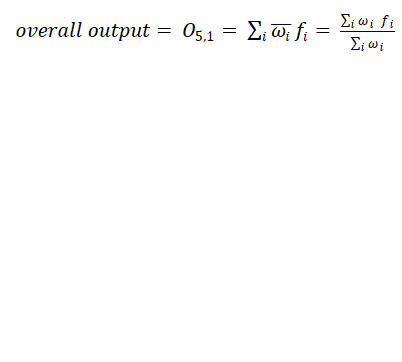image
Thus we have an adaptive network that is functionally equivalent to a Sugeno fuzzy model [17].

ADAPTIVE NOISE CANCELLATION USING ANFIS
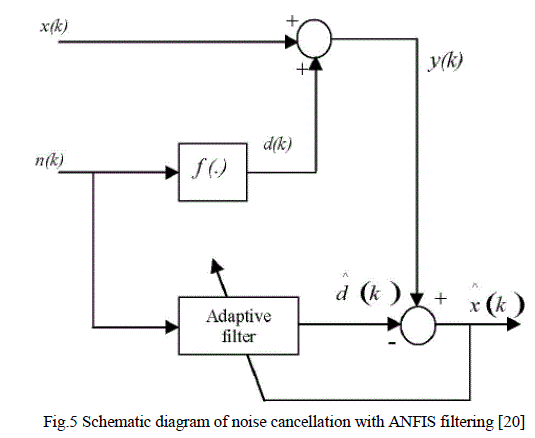
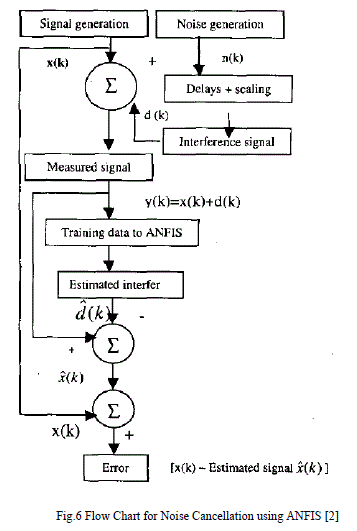
Adaptive Noise Cancellation is used to remove background noise from useful signals. This is an extremely useful technique where a signal is submerged in a very noisy environment. Usually the background noise does not keep steady and it will change from time to time. So the noise cancellation must be an adaptive process: it should be able to work under changing conditions, and be able to adjust itself according to the changing environment. The basic idea of an adaptive noise cancellation algorithm is to pass the corrupted signal through a filter that tends to suppress the noise while leaving the signal unchanged. And as mentioned above, this is an adaptive process, which means it cannot require a priori knowledge of signal or noise characteristics. Fig.5 shows the schematic diagram of noise cancellation with ANFIS filtering.
The method is used to filter out the interference component by identifying a model between a measurable noise source n(k) and the corresponding signal corrupted by interferences represented by y(k), as depicted in Fig5. The original recorded signal is x(k). To estimate the distorted noise signal d k , a clean version of the noise signal n(k) that is independent of the information signal is needed. However, one cannot access the distorted noise signal d k directly since it is an additive component of the overall measurable signal y(k).Fortunately, . as long as the information signal is zero mean and not correlated with the noise signal n(k), the detected signal y(k) can be used as the desired output for ANFIS training.
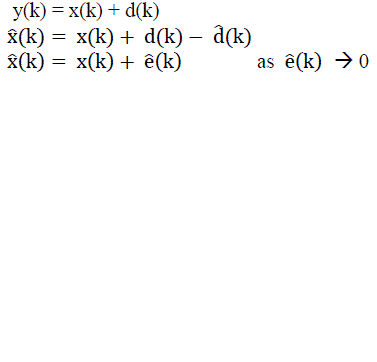image
The conditions under which adaptive noise cancellation is valid are:
a) The noise signal n(k) should he available independent of the information signal x(k).
b) The information signal x(k) must be zero mean.
c) The order of the passage dynamics is known. This determines the number of inputs to the ANRS filter. In this paper, the generalized bell membership function is used. The error cannot be minimized to zero; the minimum error is regulated by the information signal x(k), which appears as fitting noise.
Parameter settings for the ANFIS algorithm are the training epoch number is 20, the number of MFs for each input is 4, the initial step size and step size increase rate are 0.2 and 0.002, respectively, the learning algorithm is hybrid learning algorithm. For this 10000 data are used for training. The flowchart for noise cancellation using ANFIS is shown in Fig.6.

SIMULATION SET UP AND RESULT DISCUSSION
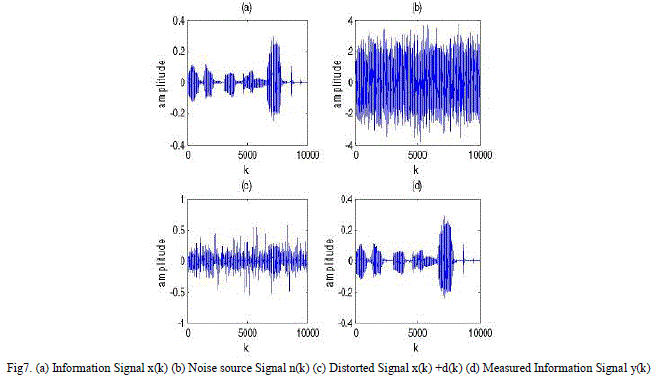
MATLAB simulation studies are carried out in this Section. Real-time recorded audio speech signal is used for performance evaluation. The signal was sampled at 8000 Hz. The noise is generated by a Gaussian noise n(k) with zero mean and unity variance. The corrupting noise d(k) is a nonlinear function, which characterizes a first-order channel dynamic, given by
d(k) = 0.6(n(k))3
The signals x(k), n(k), d(k), and y(k) are shown in Fig.7.
Hence, the measured signal used for training is given by
y(k) = x(k) + d(k)
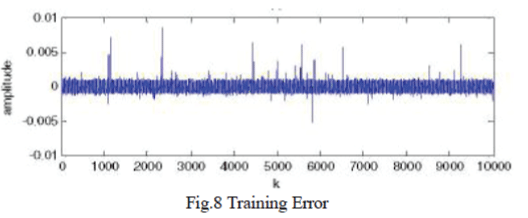
The error is then calculated by subtracting the estimated signal from the original signal as shown in Fig.8.

CONCLUSIONS
In this paper, adaptive noise cancellation using ANFIS has been implemented on audio speech signal. ANFIS is a new and intelligent method for real-time noise cancellation which is based on fuzzy logic and neural networks. This method is more efficient to eliminate noise and has faster convergence time, low computation load and fewer memory requirements.

ACKNOWLEDGEMENT
We take this opportunity to express our deepest gratitude and appreciation to all those who have helped us directly or indirectly in writing this paper.

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 5 Figure 6 Figure 7 Figure 8

References