ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Badgujar Sachin Prabhakar1, Sarode Pravin Laxmanrao1, Khatik Juber Ah. Mo. Salim1
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The influence of fuel injector nozzle is critical to the performance and emissions of diesel engine. One of the most difficult problems encountered in the development of high-speed compression-ignition engine is to have the proper atomization of the fuel in the combustion chamber during the extremely short time available. Some of the important parameters including nozzle hole size, geometry, cavitations, convergence, velocity of fuel, density of air into which fuel is injected, affects to enhance the fuel atomization. Atomization is primarily occurs due to cavitation and turbulence in the vicinity of nozzle. In this paper discharge coefficient phenomenon is used, which accounts for the different orifice approach for the better atomization such as convergence. Numerical results shows that orifice having smaller outlet diameter gives increase in the coefficient of discharge with intent of increase in cavitations up to certain range causes to increase in atomization.
Keywords |
| Cavitation, CFD simulation, Diesel injector, Discharge coefficient, Atomization |
I. INTRODUCTION |
| Modern diesel engines employ different orifice designs, and it is critical to characterize the effects of various designs on engine performance and emissions. The dynamic factors and geometrical factors controlled the flow inside injector [1].The effects of dynamic factors on the injector flow spray combustion and emissions have been investigated by various researchers [2, 3]. There have also been experimental studies about the effects of nozzle orifice geometry on fuel injection and spray behaviour. |
| Design of the injector nozzle is critical to the performance and emissions of modern diesel engines. Some of the significant injector nozzle design parameters include nozzle hole size, shape, details of the injector seat, the injector sac. These features were affects the combustion characteristics of the diesel engine and stability of the emissions. |
| The fuel is injected in a cone shaped spray through a nozzle. The spray can be divided into different regions based on the composition of the two phase flow which are shown in Fig.1. The liquid phase of a spray with high pressure injection system continually disintegrates into small droplets very close to the nozzle and produces droplets with different sizes. The injection pressure is a very important parameter for atomization. The primary atomization, which is the breakup of the intact liquid phase into first droplets, occurs in the direct vicinity of the injection nozzle orifice. Later on, the relatively large initial droplets can be further broken up into smaller secondary droplets [4]. |
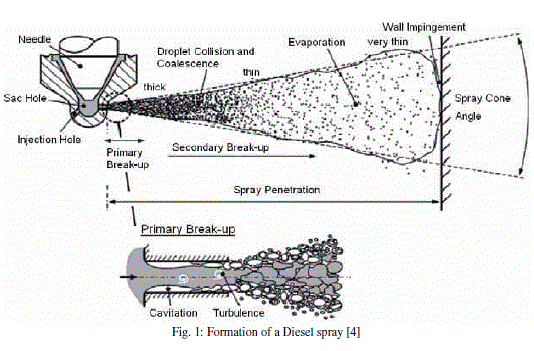 |
| As the primary atomization is occur in vicinity of orifice due to turbulence and cavitation, so there is importance of orifice shape which affects on atomization. It is well known that cavitation in a nozzle hole is important for increasing turbulence and improving atomization also there is danger of excessive cavitation giving very poor atomization [1]. Cavitation is a phenomenon encountered mainly in liquid pumps and turbines, injection nozzles, throttles, pipes and ship propellers. Cavitation can also decrease the flow efficiency (discharge coefficient) due to its effect on the exiting jet, by partially blocking the nozzle exit. Also, the implosion of cavitation bubbles inside the orifice can cause to decreasing performance of the injector. It was clear that optimal amount of cavitation is desirable, and so is important to understand the causes for cavitation generation [2]. |
II. LITERATURE SURVEY |
| The literature survey regarding nozzle with fuel atomization aspect investigated are reviewed and discussed in this chapter. |
| John C. Kayseret.al studied the discharge coefficients for both rounded and elliptical entry nozzles correlate well with a throat Reynolds number. The correlation shows that as the Reynolds number is decreased the discharge coefficient drops precipitously for Re <20,000. For Re > 20,000 the discharge coefficient increases slowly with increasing Reynolds number. This behaviour is consistent with both previous data and fluid dynamics theory for rounded and elliptical entry nozzles [5]. |
| J. Konget.al, investigated that tapered nozzle hole increases the discharge coefficient and reduces the cavitation in the hole. The velocity and particle size of droplets were measured using a phase Doppler anemometer system. The result shows that injection rate shape that initial increasing slope of injection velocity from tapered nozzle hole was higher than that of straight nozzle under the same injection pressure. Spray tip penetration increased with tapered nozzle hole because of higher initial injection velocity. And at the vicinity of nozzle hole exit, spray angle decreased with tapered nozzle hole because of strong spray axial momentum. Sauter mean diameter (SMD) at the downstream value with tapered nozzle hole was smaller than that of straight nozzle hole due to higher initial injection and increased air/fuel momentum exchange [6]. |
| H. S. Sondh et.al investigated that the variable area orifice meter indicates the flow rate as a linear displacement of a symmetrical body placed concentrically downstream of an orifice inside a constant area duct. Three shapes of symmetrical body namely, a frustum of cone, frustum of cone with hemispherical base, and frustum of cone with hemispherical base and parabolic apex are used downstream of an orifice to develop a variable area orifice meter. Experiments have been performed at different positions of the symmetrical bodies to evaluate the performance of the variable area orifice meter. The frustum of cone having hemispherical base and parabolic apex gives nearly linear variation of the flow rate with its position for a constant pressure differential [8]. |
| A. Dorri et al carried out a numerical investigation, in order to evidenciate the effects of the hole shape in the generation of the spray, in high pressure diesel nozzles. Different hole shapes are tested using the finite volume CFD code at different fuel injection pressures. After studying the CFD simulations of pressure contours, the flux line, velocity vectors and the mass flow rate of the fuel inside the nozzle, results have shown that conicity of holes changes with the variation of pressure inside the holes [9]. |
III. CAVITATION PHENOMENON |
| One of the main factors affecting nozzle discharge coefficient and the momentum of the injected fuel jet is cavitation in the nozzle hole. This is especially the case in straight round holes with a sharp edged entrance. Geometricinduced cavitation occurs when the local pressure drops below the vapour pressure and a vapour phase forms. When cavitation occurs in the nozzle hole the flow becomes choked [10]. |
| Cavitation in a fuel injector nozzle improves the atomization through primary break up, and subsequently improves the combustion of fuel, which reduces emissions [7]. Better atomization facilitates reduction of hydrocarbon emissions and improves the engine efficiency |
| Determination of the cavitation number |
| It was lined out that cavitation influences the coefficients Cd and ηM. To estimate the influence of the cavitation, a cavitation number can be defined. The rate of cavitation depends on the pressure drop across the nozzle orifice |
| K = (Pi - Pv)/ (Pi - Pb) (1) |
| Where Pi is the pressure at the inlet of the nozzle hole. Other definitions of cavitation number are also used. Cavitation occurs when the cavitation number defined by Equation (1) is below a critical value, Kcrit that depends on pressure and nozzle details. While Equation (1) is easier to use in that all the pressures can be either measured or estimated, Kcrit must be determined experimentally or numerically. Cavitation will occur at most conditions in fuel injection systems utilizing straight nozzle holes with a sharp edged entrance [2]. |
| Cavitation occurs when the cavitation number is less than Kcrit. Under these conditions, Cd is seen to vary with√ . At K~1, Cd reaches a minimum value that is equal to Ca. In summary, under cavitating conditions: |
| Cd = Ca √k (2) |
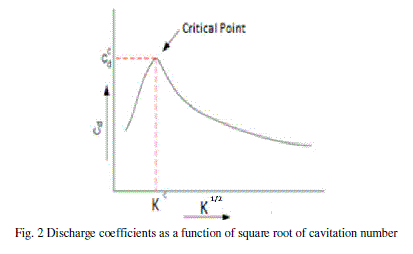 |
| Since cavitation has a major influence on the discharge coefficient of the baseline straight nozzle with a sharp edged inlet, it is worth considering what can be done to reduce or even eliminate cavitation in the nozzle and what effect that would have on the performance of the nozzle hole[3]. |
| For conical holes, it is common to describe the hole in terms of the diameter difference between the inlet and outlet using the factor: |
| K -factor = (Dentry – Dexit)/10 |
| Where Dentry and Dexit are in μm, it is called as “K-factor”. This parameter causes the diameter difference between the inlet and outlet. |
| IV. NOZZLE UNDER INVESTIGATION |
| Nozzle was to be taken having fixed outlet diameter 219 μm and changed inlet diameter for conicity. The cavitation and coefficient of discharge phenomenon can be taken in the orifice section. So numerical analysis can be done with the help of gambit and fluent combination and analyse the results. Gambit is the mesh developer software in which we can create model and mesh it. Fluent is the analysis software in which different models are used to solve the model, here we are taking spalart allmaras one equation for analysis. |
| A. Gambit Process |
| Orifice was divided into six parts namely Inlet, inner wall, upper wall, outer wall, outlet and axis. In order to capture the flow parameters at orifice inlet and outlet, which are critical portions, a finer mesh was done near these points. For convenience, axis symmetric nozzles were simulated and the Injection pressure of the nozzle used was kept at a same range as the real fuel injector nozzles i.e. 100 bar. |
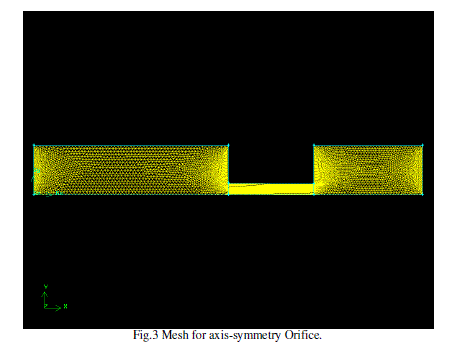 |
| B. FLUENT Process |
| After gambit process is over mesh file will be write. Fluent reads that mesh file after which boundary conditions are applied. A series of simulations were performed at various inlet diameters. The simulations were performed until a stable mass flow rate at the inlet and the outlet is attained. |
| Following boundary conditions were applied. |
| Operating conditions: 101325 Pa |
| Solver: Green Gauss cell based, 2d, steady, implicit, Pressure based |
| Model: spalart allmaras [one equation] |
V. RESULTS OF CFD SIMULATIONS |
| The nozzle consist of cylindrical hole shape with same inlet and outlet diameter having zero K-factor. The simulations carried out considering this geometry shape to get the discharge coefficient, total pressure, axial velocity distributions and contours of it. |
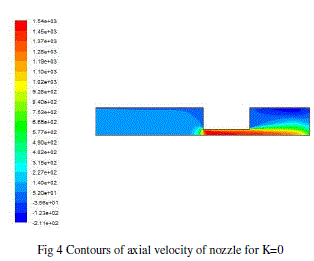 |
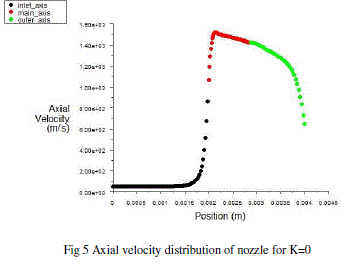 |
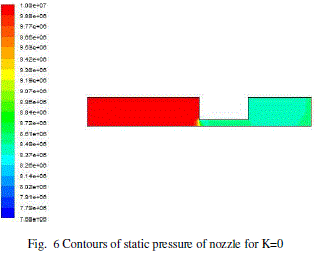 |
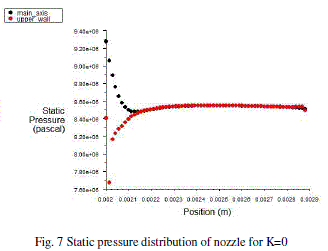 |
| The different nozzle geometry is used to get discharge coefficient such as 0.7 and 1.0 K-factor. The comparative discharge coefficient distribution shown in figure 10. |
VI. CONCLUSIONS |
| Cavitation is the main source for primary atomization in the vicinity of nozzle. Higher the cavitation smaller are the droplets but it was cause to decrease in the velocity that flow. So cavitation is also keep upto critical condition and this condition is achieved by increasing the discharge coefficient. From the present investigation the following main conclusions can be drawn. It was seen that the coefficient of discharge was increases with increase in conicity of nozzle. The convergent shape towards the exit greatly modifies the coefficients of discharge during the injection process in different types of nozzles and thus the cavitation forms up to critical cavitation. |
ACKNOWLEDGMENT |
| I wish to express my sincere gratitude to Prof. P. L. Sarode for their guidance and encouragement in carrying out this work. I also grateful to my friends who gave me their support. |
References |
|