Investigation of the Effect of Partial Heating
in an Internally Heated Vertical Annulus

Shahid Husain; Jawed Mustafa; M Altamush Siddiqui

doi:DOI: 10.15680/IJIRSET.2015.0405112

Investigation of the Effect of Partial Heating in an Internally Heated Vertical Annulus

Shahid Husain¹, Jawed Mustafa² and M Altamush Siddiqui³

Research Scholar, Department of Mechanical Engineering, Zakir Husain College of Engineering and Technology, A.M.U, Aligarh,U.P, India
Guest Faculty, Department of Mechanical Engineering, Zakir Husain College of Engineering and Technology, A.M.U, Aligarh,U.P, India
Professor, Department of Mechanical Engineering, Zakir Husain College of Engineering and Technology, A.M.U, Aligarh, U.P, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Numerical Analysis has been carried out for transient two dimensional heat transfer and fluid flow during natural convection of a fixed Prandtl number (0.71) fluid through an internally heated vertical annulus. The governing continuity, Navier stokes and energy equations have been solved using finite volume SIMPLER technique. The governing equations are solved on a staggered mesh. The solutions are obtained for an aspect ratio of 10 and radius ratio of 2 by varying the heating length from full to 50%. The MPI parallel programming technique was used for domain decomposition and parallelization of code. The transient behavior of the system has been discussed in detail.

Keywords

Annulus, Natural Convection, Partial heating, SIMPLER, Transient.

INTRODUCTION

The buoyancy induced flow occurs in geophysical, astrophysical and environmental phenomena and is also made use of in solar energy devices, thermo-siphons, nuclear reactors and in the cooling of electronic equipments and turbine blades.In the last few decades, significant interest has been shown on the modelling and control of thermal convection loops. The absence of moving components drastically reduces the probability of a failure in the removal of heat from the source. Infact, this is the main reason why natural convection is preferred to forced convection in Nuclear energy plants where safety is a primary requirement. The refrigeration of reactors in nuclear power plants and electrical machine rotor cooling therefore represent the main applications of closed-loop thermosyphon. Some important applications in which closed-loop thermosyphons are preferred to forced circulation loops are those in which the absence of pumping elements allows a considerable cost reduction, like in geothermal plants or solar heaters that have low-temperature thermal sources but a relatively high circulating flow rate or, finally, where the pumping system cannot be conveniently positioned, as incooling systems for internal combustion engines, turbine blade cooling or computer cooling. The natural convection heat transfer in vertical annuli has also a wide application in the field of engineering. The annulus represents a common geometry employed in a variety of heat transfer systems, ranging from a simple heat exchanger to the most complicated nuclear reactors[Sankar and Younghae (2010)].

Numerical studies have been performed by many researchers on the internally heated vertical annulus. El-Shaarawi and Khamis [1987] investigated the laminar natural convection through an open-ended vertical annulus with a rotating inner cylinder, with one uniformly heated boundary and one adiabatic boundary. The boundary-layer equations have been solved using finite-difference scheme for a fluid of Pr = 0.7 in an annulus of radius ratio 0.5.Quere and Pecheux [1989] have examined numerically the behavior of the solutions of the Boussinesq equations in a tall, differentially heated, air filled annulus. Kumar and Kalam [1991] performed numerical investigation of natural convective heat transfer of a fluid in a vertical cylindrical annuli with inner wall maintained at higher temperature than the outer cylinder while the top and bottom plates are insulated. They performed numerical analysis for 10< Ra <106, 1< k < 5 and 0.3< A <10 and compared the results with experimental data and developed correlation for heat transfer rate. El Shaarawi and Al-Aattas (1992) developed a finite-difference scheme for solving the boundary layer equations during the unsteady laminar free convection flow in open ended vertical concentric annuli. The Numerical results for a fluid of Pr= 0.7 in an annulus of radius ratio 0.5 were presented showing the developing velocity and pressure fields with respect to space and time. Sankar [2008] performed a numerical study of laminar double-diffusive natural convection in an open ended vertical cylindrical annulus with unheated entry and unheated exit.Sankar [2008] solved the steady continuity, momentum and energy equations using finite difference technique.Sankar in his study considered uniform wall temperatures, uniform wall concentration, uniform heat flux and uniform mass flux on both boundaries. The results show that there is a severe effect of the unheated entry and exit on the heat and mass transfer rates. Sankar and Younghae [2010] investigated the effect of discrete heating on convection heat transfer in a vertical cylindrical annulus. The numerical results show that the heat transfer rate was always higher at the bottom heater, which increases with the radii ratio and decreases with the aspect ratio. Venkata Reddy and Narasimham [2008] performed a numerical study of the conjugate natural convection in a vertical annulus with a centrally located vertical heat generating rod. The formulation in primitive form is solved using a pressure-correction algorithm. The average Nusselt numbers on the inner and outer boundaries show an increasing trend with the Grashof number. Wang et al. [2012] developed a finite volume model and analyzed transient natural convection in closed ended vertical annuli, with isothermally heated (or cooled) inner surface and insulated horizontal and outer surfaces. Lopez et al. [2012] performed finite difference numerical analysis of Natural convection in a closed ended annulus with a discrete heat source on the inner cylinder while the outer cylinder is cooled isothermally; the top and bottom walls and unheated portion of the inner cylinder are assumed as insulated.

The present numerical analysis solves the unsteady continuity, momentum and energy equations using finite volume method and deals with transient aspects of the flow. The study considers open ended annulus of aspect ratio 10 and radius ratio 2, the annulus being full heated and partial heated. When the annulus is considered as partially heated, the middle length is heated while the entrance and exit are unheated. The annulus being heated 98% of the total length means there is 0.01L (x=1%) unheated portion at the entrance and 0.01L unheated portion at the exit. Similarly, for 90% heated length, there will be 0.05L (x=5%) at the entrance and 0.05L at the exit that will be unheated, and so on.

FORMULATION AND SOLUTION

Since, the flow is in annulus a cylindrical coordinate system, as shown in Fig. 1, is selected.The changes in properties are not significant so constant fluid properties with negligible viscous dissipation are used in the analysis. The variation of density is taken into account only in the body forces (Boussinesq approximation). Following are the nondimensional parameters:

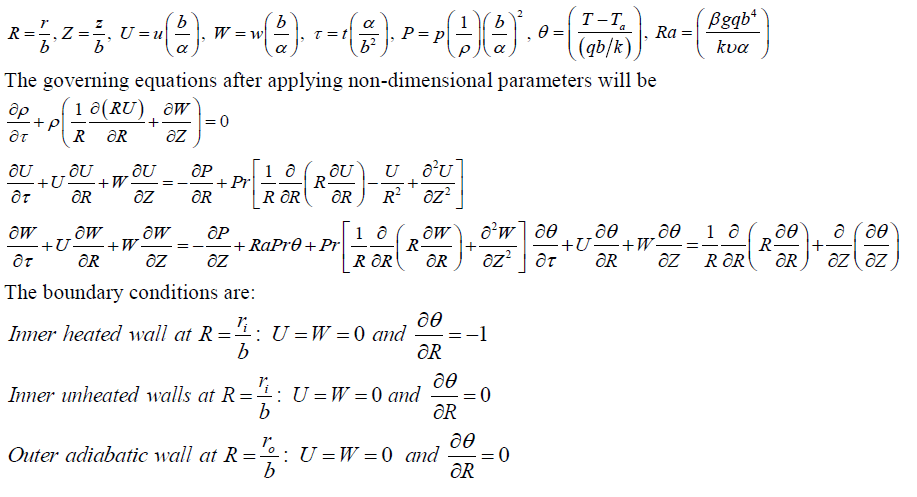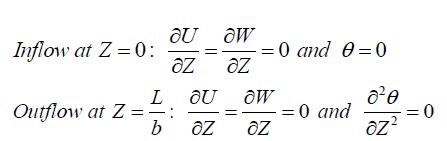The model equations are nonlinear and could not be integrated exactly, so the system of equations are solved numerically by using Finite Volume SIMPLER technique. An implicit formulation is used and the resultant equation so formed is solved by Thomas algorithm. The first step in the finite volume method is to divide the domain into discrete control volumes. The boundaries (or faces) of control volumes are positioned mid-way between the adjacent nodes. Thus each node is surrounded by a control volume or cell. It is common practice to set up control volumes near the edge of the domain in such a way that the physical boundaries coincide with the control volume boundaries.

A general nodal point is identified by P as shown in Fig.2 and its neighbour’s in a two-dimensional geometry. The nodes to the west, east, north and South are identified by W, E, N and S respectively. The west side face of the control volume is referred as 'w' and the east side control volume face by ‘e'. The north side face of the control volume is referred as 'n' and the south side control volume face by ‘s’. The distances between the nodes W-P, P-E, P-N andP-S are identified by , , PW PE PN PS δX δX δY and δY respectively. Similarly the distance of point P from face w, face e, face n and face s are denoted by , , Pw Pe Pn Ps δX δX δY and δY respectively. Thus the control volume dimensions, in Fig.2 are identified. In the present case a control volume based finite difference method is used. The hybrid scheme, which is a three line approximation of exact solution curve has been chosen because of its simplicity.

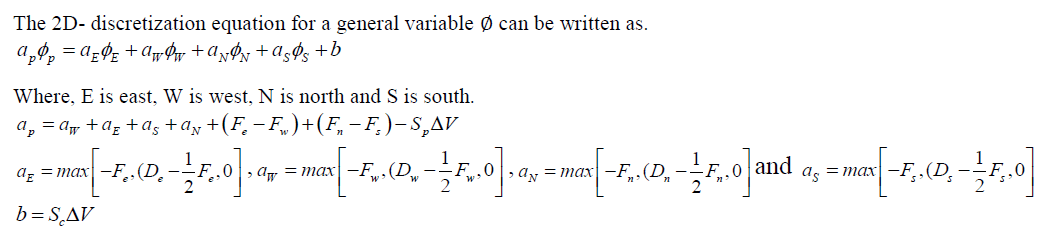RESULTS AND DISCUSSION

The computations were performed for fixed values of Prandtl number, Rayleigh number, aspect ratio and radius ratio as 0.71, 103, 10 and 2 respectively. The analysis was done for full heating, 98%, 90%, 80%, 70%, 60% and 50% percent heating of the total length of the inner wall.The transient behavior of the axial and radial velocity, temperature and pressure profiles along axial and radial directions are presented in the result. Transient nature of velocity, temperature and pressure taken at the exit for different heated lengths are also presented. Pressure and temperature along the annulus and Temperature, axial and radial velocities at inlet, mid-height and exit along the radial direction are discussed for different heating lengths of the annulus.

1. Temperature, pressure and axial velocity along the annulus at different times until steady state

Figure 3 shows the development of temperature profile in axial direction for fully heated and 80% centrally heated annulus. Initiallythe temperature is almost constant in the heated section of the annulus.As time elapses, the constant temperature decreases attaining a linear trend during the steady state. Near the entrance the temperature is initially high but decreases with time because initially conduction dominates the convection until the flow becomes fully developed. The effect of unheated (adiabatic) entrance and exit can be seen in the Fig. 3(b).

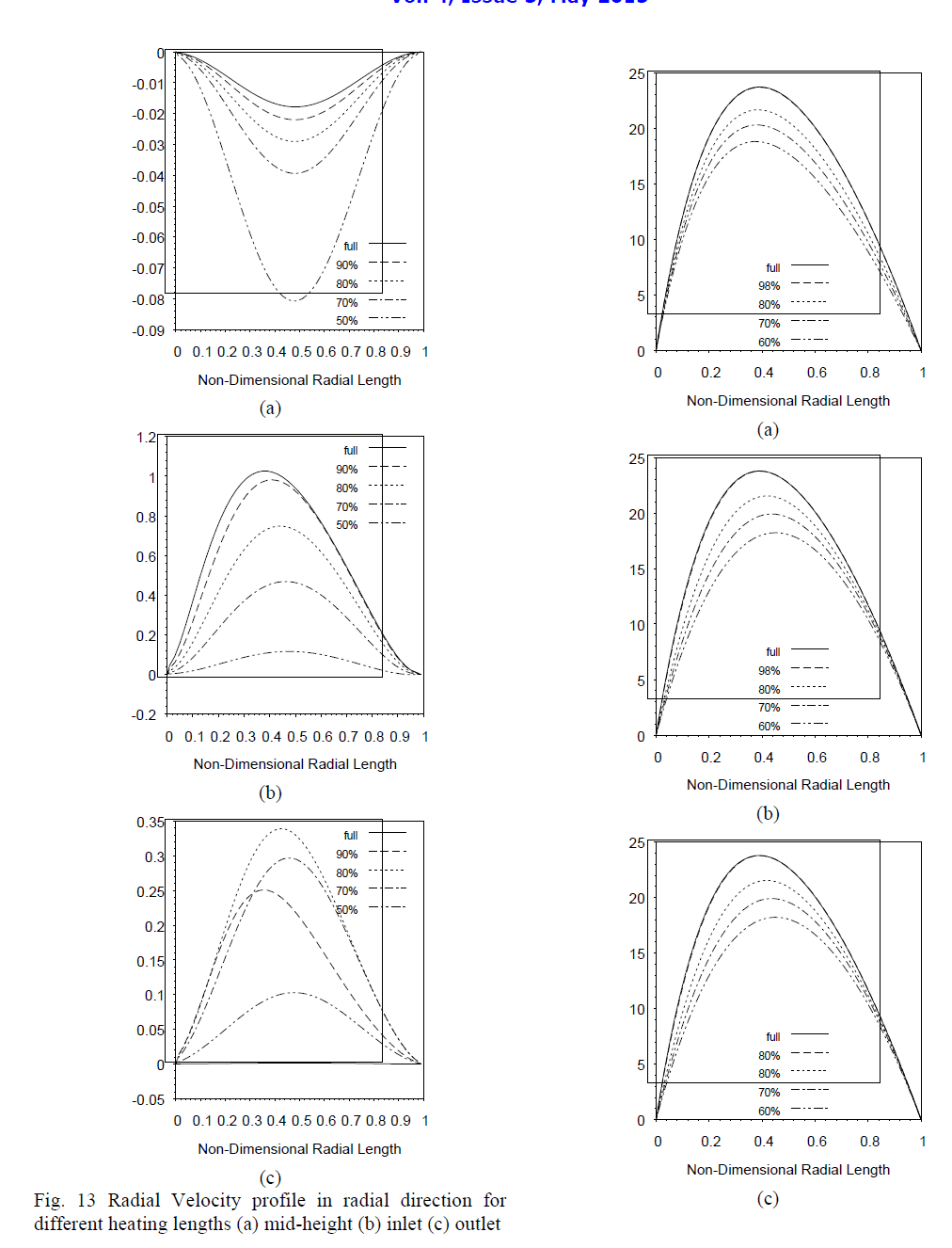Fig. 14 Axial Velocity profile in radial direction for different heating lengths(a) mid-height (b) inlet (c) outlet At the exit of the annulus, with full heating the temperature decreases from the heated wall and becomes constant at the outer wall. However, with partial heating the temperature lowers down and becomes constant throughout as shown in Fig. 12(b).Figure 13 shows variation of the radial velocity inthe radial direction at inlet, mid height and exit of the section.

At mid-height, [Fig. 13(a)] the radial velocity is negative. It decreasesfrom the inner wall, reaches to a minima and then increases up to the outer wall. This decrease in velocity increases as the heating length decreases. With full heating the radial velocity is close to zero approaching the fully developed flow region. At inlet, the radial velocity, shown in Fig. 13(b), is positive which increases from the inner wall, reaches to a maxima and then decreases up to the outer wall. This velocity decreases as the heated length decreases. At the outlet, the radial velocity shown in Fig. 13(c) again becomes positive but of lesser magnitude as at the inlet. With full heating, the radial velocity is zero showing that the flow has become fully developed. However during partial heating, radial velocity exists.

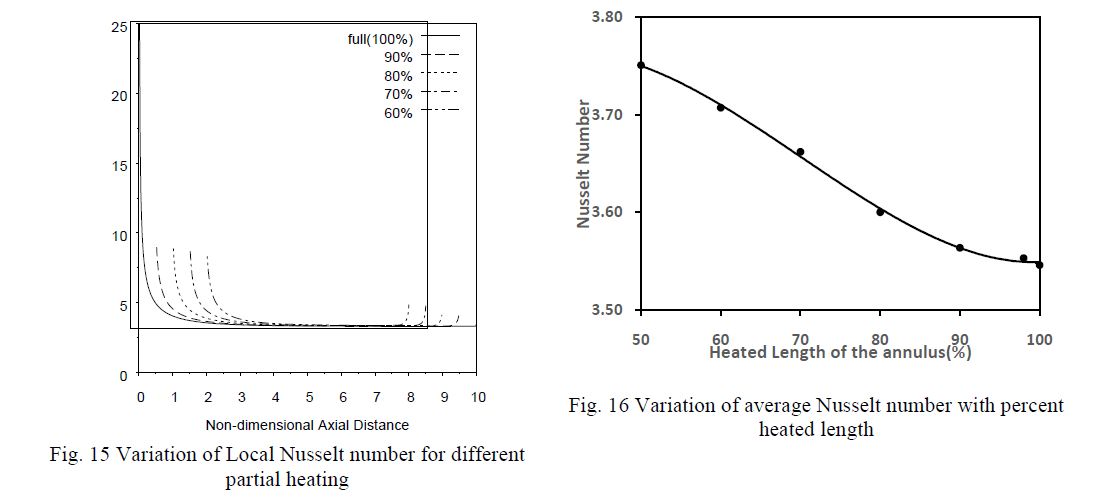Figure 14 shows variation of the axial velocity with time for different heated lenghts. At inlet, mid-height and outlet the axial vecocity is zero at inner wall increases to a maxima and then decreases becoming zero at the outer wall. As heated length decreases the magnitude of axial velocity also decreases.Figure 15 shows the variation of local nusselt number along the annulus. The local nusselt number decreases from high value at the start of heating and then becomes constant for remaining heated length. These variations in the nusselt number thus represent the developing boundary layer.

The initial high value of nusselt number is decreases with increase in unheated length although the constant value attained is same for all cases. At the point where heating ends some increase in local nusselt number is observed. Figure 16 shows the variation of average nusselt number with increase in heated length. The average nusselt decreases gradually with increase in heated length.However, the decrease in nusselt number is not very significant.

Conclusion:

The following conclusion is drawn from the results presented. With decrease in heated length

1) Axial velocity at outlet decreases and time taken to achieve steady state remains same.

2) Temperature at exit decreases and time taken to achieve peak value increases.

3) Fluctuations in pressure are observed near the entrance whose magnitude first increases and then decreases.

4) At mid-height the negative radial velocity increases while at inlet it decreases.

5) Average value of Nusselt number increases gradually.

NOMENCLATURE

References

S.V. Patankar, Numerical heat transfer and fluid flow, in: W.J. Minkowycz, E.M. Sparrow (Eds.), Series in Computational Methods in Mechanics and Thermal Sciences, Hemisphere Publishing Corporation/ McGraw-Hill Book Company, Washington/New York, (1980).
M. A. I. El-Shaarawi and M. Khamis,, Induced flow in uniformly heated vertical annuli with rotating inner walls, Numerical Heat Transfer, vol. 12, 493-508, (1987).
Ranganathan Kumar and M. A. Kalam, laminar thermal convection between vertical coaxial isothermal cylinders. Int. J. Heat Mass Transfer 34, vol. 2, 513-524, (1991).
M. A. I. El-Shaarawi and M. A. Al-Attas, Unsteady natural convection in open-ended vertical concentric annuli, Int. J. Num. Meth. Heat Fluid Flow, vol. 2 503-516, (1992).
P. Venkata Reddy, G.S.V.L. Narasimham, Natural convection in a vertical annulus driven by a central heat generating rod, International Journal of Heat and Mass Transfer-51, 5024–5032,(2008).
M. Sankar, Numerical Study of Double Diffusive Convection in Partially Heated Vertical Open Ended Cylindrical Annulus, Advances in Applied Mathematics and Mechanics, Vol. 2, No. 6, pp. 763-783, (2010).
M. Sankar and Younghae Do, Numerical simulation of free convection heat transfer in a vertical annular cavity with discrete heating,International Communications in Heat and Mass Transfer 37 600–606, (2010).
M. Sankar, M. Venkatachalappa, Younghae Do, Effect of magnetic field on the buoyancy and thermocapillary driven convectionof an electrically conducting fluid in an annular enclosure, International Journal of Heat and Fluid Flow-32, 402-412,(2011).
Shimin Wang, Amir Faghri and Theodore L. Bergman, Transient Natural Convection in Vertical Annuli: Numerical Modeling and HeatTransfer Correlation, Numerical Heat Transfer, Part A, 61: 823–836, (2012).
J M Lopez, M Sankar and Younghae Do, Constant-flux discrete heating in a unit aspect-ratio annulus, Fluid Dyn. Res. 44-065507 (18pp), (2012).