ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
V.Krishnasamy 1 , R.Kalpana devi 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
CuSO4.(NH4)2 SO4. 4H2O and ZnSO4.(NH4)2 SO4. 6H2O.were taken for the experiment. They were mixed in various proportions , dissolved in the required quantity of water in hot condition and allowed to crystallize in various temperatures in a thermostat Then they were separated , dried and weighed ; from the weight of mixture and the weight of water molecules , the percentage of water molecules in the each crystal was calculated by gravimetric method. Unexpected wonderful results were obtained
Keywords |
| isomorphous , thermostat , gravimetric, crystallization, silica crucible , separation , filtration, mixed crystal , |
INTRODUCTION |
| The property of a substance depends on so many factors like atmosphere , temperature , water of hydration , if it is a hydrated substance , pressure etc.,. In that way in this research we try to prepare some hydrated salts with their abnormal hydrated state. For that we have taken two salts , Copper Ammonium Sulphate and Zinc Ammonium Sulphate ; normally they have Four and Six water molecules respectively. Their molecular formulae can be written as CuSO4.(NH4)2 SO4. 4H2O and ZnSO4.(NH4)2 SO4. 6H2O. Therefore it is really not only very interesting but also very useful to have Hydrated Salts with different water of Hydration.. Here the two salts are taken as a mixture of different proportions. They are dissolved in the required quantity of water in hot condition and allowed to crystallize in a thermostat. Same amount of mixture is dissolved in different quantity of water and the same procedure is followed. The experiment is done in different temperatures , starting from room temp. Then water of hydration is determined by gravimetric method. In order to form isomorphous crystals two substances must have the same chemical formulation, they must contain atoms which have corresponding chemical properties and the sizes of corresponding atoms should be similar. These requirements ensure that the forces within and between molecules and ions are approximately similar and result in crystals that have the same internal structure. The structure and water of hydration , of a salt mixture depends on so many factors like , temperature , concentration of each salt in the solution , pressure , Catalyst , procedure adopted , velocity of the reaction conducted, etc., In a crystal containing a mixture of isomorphous substances, each substance brings its own influence, which may be made to predominate in turn according to the proportions of the mixture.Isomorphous substances are closely similar in shape. Double Sulphates such as Tutton's salt, with the generic formula MI 2MII(SO4)2.6H2O, where MI is an alkali metal and MII is a divalent ion of Mg, Mn, Fe, Co, Ni, Cu or Zn form a series of isomorphous compounds which were important in the nineteenth century in establishing the correct atomic weights of the transition elements. Alums , such as KAl(SO4)2.12H2O, are another series of isomorphous compounds, though there are three series of alums with similar external structures, but slightly different internal structures. Many Spinels are also isomorphous. when a pair of isomorphous salts is crystallized together from an aqueous solution , a solid of homogenous composition results. In such a ternary system the compositions of both the aqueous and solid phases are continuously changing during the course of crystallisation. A study of the distribution of the salts between crystallisation the aqueous and solid phases is of considerable importance both from theoretical and practical aspects of fractional crystallisation. Further two types of system – equilibrium and nonequilibrium are encountered during fractional crystallisation. Crystallization carried out rapidly and stopped at the end of a short period ( a few hours ) always leads to a system in a state of non-equilibrium , ie., no equilibrium is attained between solid and aqueous phases with respect to the composition of salts in the two phases , though the process of crystallization itself is complete. If the non-equilibrium system is kept in an isothermal condition for sufficiently long periods, recrystallisation begins. This finally gives rise to a system in equilibrium in which the composition of aqueous and solid phases do not change even if the two phases are in contact with each other for any length of time. Then the crystals were analyzed by titrometry technique. Many equations suggested for co-crystallization of salts, in equilibrium and non-equilibrium conditions . Berthelot - Nernst1 law for cocrystallisation of Radium with Barium nitrate is given by, C S / CL = KN ---------- (1) Where C S and CL represent the concentration of Radium ion in solid and liquid phases in micro levels ; KN represents the Distribution constant. Khlopin 2-12 has written the equation in the following form X ïÃÂòS / m S = KN ( 1 – x ) ïÃÂòL / m L --------- (2) where x is the fraction of the micro-component in the solid phase. ïÃÂòS and ïÃÂòL are the dencities of the solid and liquid phases respectively. m S and m L are the amounts of the solid and liquid phases respectively. Henderson and Kracek 13 has written the equation in the following form X / Y = D ( a – x ) / ( b – y ) -------- (3) Where X and Y are the amounts of the solid and liquid phases respectively.a and b are respectively the initial amounts of the micro and macro components in solution; D is the Distribution constant. D and K are related by the equation , D = KN ( 1 – mx ) ïÃÂòL / m L ----------- (4) Where ( 1 – mx ) ïÃÂòL / m L is the concentration of the macro component expressed in gm/ml of the solution. Doerner and Hoskins14 gave a different equation for coprecipitation of Radium ion and Barium sulphate. Each layer in a crystal should satisfy the following equation dy/dx = λ * y/n ------------- ( 5 ) the logarithmic equation of Doerner and Hoskins : ln Y /a = λ ln n / b -------------- (6) where n and y are the concentrations of Barium and Radium ions respectively in solutions at any instant. dy and dn are the amounts of radium and barium ions respectively precipitated as sulphates at this instant. λ is a constant known as Distribution Constant of the impurity. Doerner and Hoskins law does not assume a true equilibrium between crystals and the solution at the end of crystallization , but postulates a uniform layer like distribution of impurities in the solid phase, with a momentary equilibrium between the crystallizing layer and the solution. These laws have been thoroughly checked with experimental data. Using different methods , Kholpin has evaluated for several systems the values of D and KN are constant ; thus Kholpin has shown that true equilibrium has been attained in these systems and the value on KN is independent of the way in which equilibrium was reached. A similar conclusion has been reached by Hahn , who investigated radium chloride and Barium chloride. His results have confirmed that the Berthelot – Nernst law is applicable to the distribution of an electrolyte between crystalline and liquid phases. D is sensitive to variation in temperature of the system Roozeboom15 has classified systems of two isomorphous salts A & B , varying in respect of only one ion , which constitute ternary systems with water , forming continuous solid solutions. The classification is based on the relative distribution of salts between liquid and solid phases. In type I , the mole fraction of one of the salts , say A , is always greater in the liquid than in the solid phase, over the entire range of concentration of the system .ie., Y is always greater than X. |
| In type II , Y is greater at lower concentrations of A and then becomes smaller than X for the range of concentrations approaching pur A. Type III is just the reverse of type II, ie., Y is smaller than X at low concentrations of A and becomes larger than X at larger concentrations of A . |
II.OBJECT AND SCOPE OF THE PRESENT STUDIES |
| The object of the research is to know whether the salts taken for study are forming with abnormal water of hydration or not ; if it forms , under what condition they form and what are the number of molecules of hydration ? whether they are having the same number of water molecules as any one of the salts in the mixture or totally different number of water molecules . |
III.EXPERIMENT |
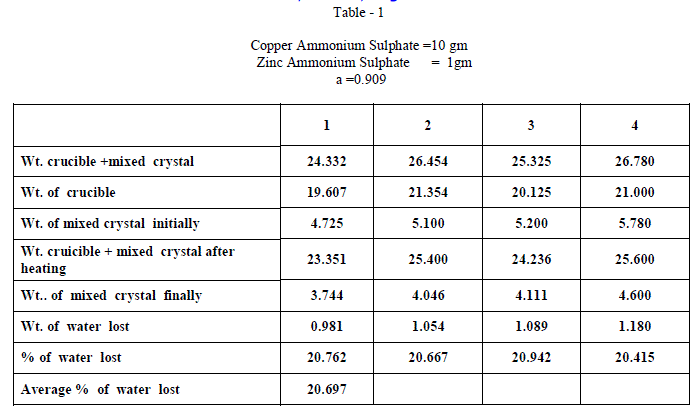
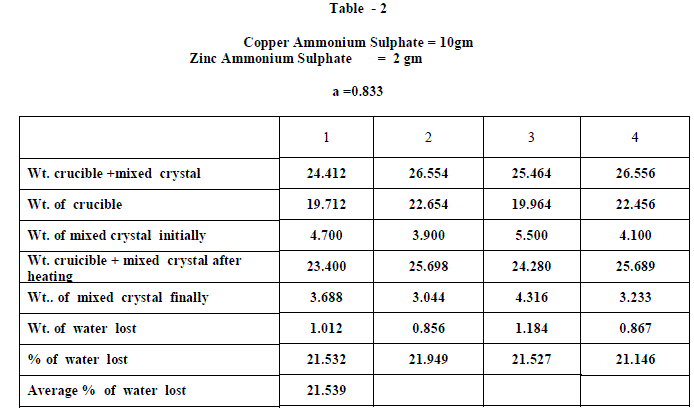
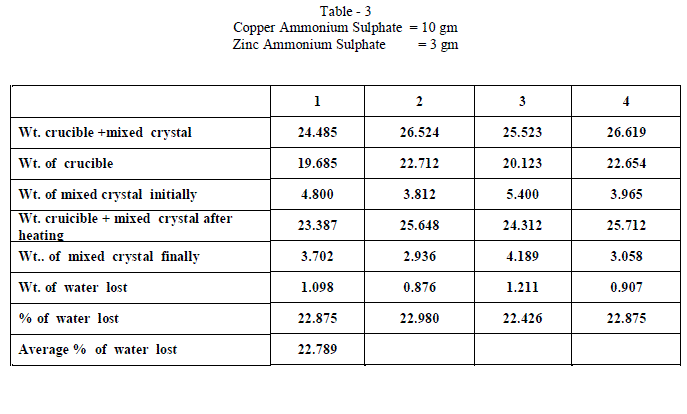
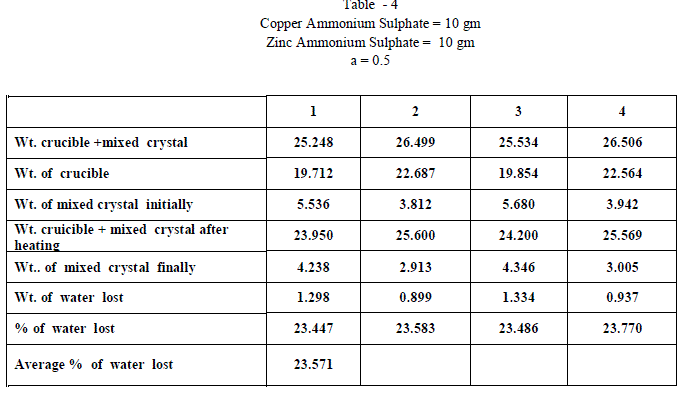
| Copper Ammonium Sulphate and Zinc Ammonium Sulphate were of BDH AR grade and used without any further purification and distilled water was used in all the experiments. Experiments on fractional crystallization were designed to obtain different values of ‘w’ ( fraction by weight of the crystals separating from the solution ) for a given ratio of the two salts in the initial mixture. This was done by preparing mixtures of the two salts corresponding to , a = 0.909 , 0.833, 0.7692 , 0.5 , 0.400, 0.3704 , 0.1667 , 0.1 crystallizing the mixtures from solutions containing different amounts of water. In all experiments crystallization was allowed to proceed only for 6 hours which ensured the non – equilibrium state of systems. The general experimental procedure adopted was as follows : A clean and dry Pyrex flask ( about 100 ml capacity ) fitted with a good ground glass stopper was weighed. Suitable amount of the two salts were weighed accurately and added into the flask. An appropriate amount of water was added and the flask was weighed again. The flask was gently heated with the stopper on to dissolve the salts completely. It was then kept in the bath maintained at 28âÃâæ c .± 0.5 âÃâæc Crystallization was generally found to occur within 15 minutes ; when it is not occur spontaneously , the solution was seeded with a tiny crystal of the less soluble salt. The flask was kept in the thermostat for 6 hours. At the end of six hours , the flask was removed from the thermostat and the outer surface was quickly wiped dry with filter papers. The mother liquor was rapidly but carefully decanted . The moist crystals were dried off. A clean Silica Crucible is heated in an electric Bunsen and allowed to cool in dessicator. When quite cold , it is weighed accurately. All the mixed crystal obtained in each and every experiment were then placed in the crucible and weighed accurately. The crucible is placed in the electric Bunsen and heated strongly for about twenty minutes. Then it is allowed to cool in a dessicator for half an hour and then weighed accurately. From the loss in weight , we can calculate the percentage weight of water in the mixed crystal . |
 |
 |
 |
 |
 |
 |
 |
 |
IV.RESULTS AND DISCUSSION |
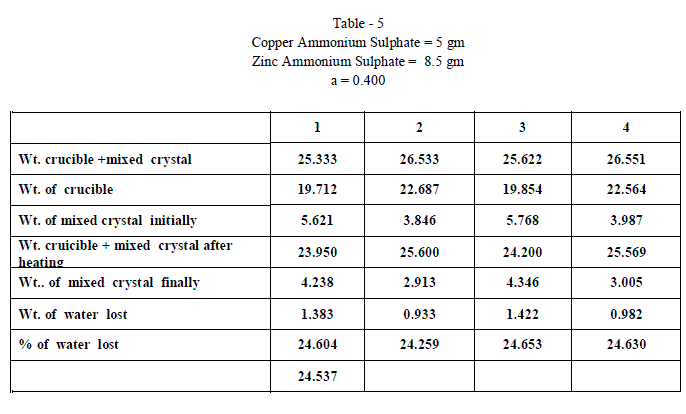
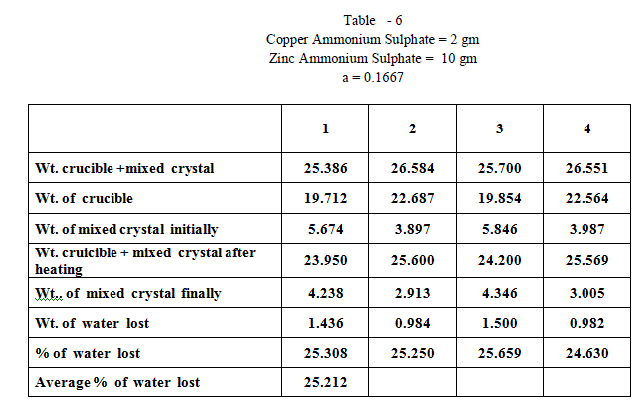
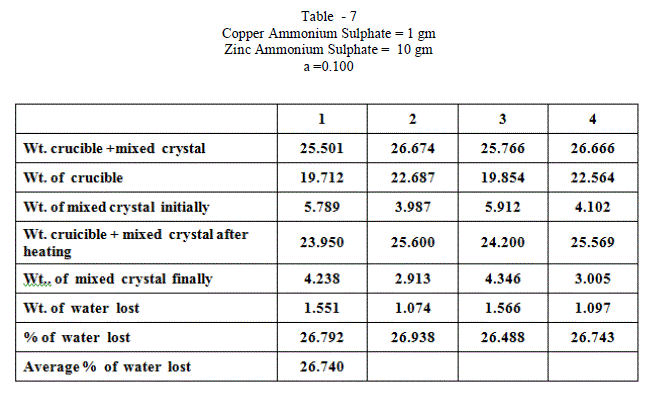
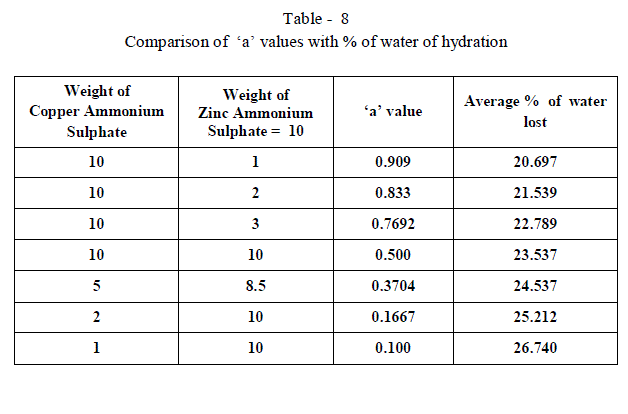
| When isomorphous crystals are mixed in different proportions and allowed to crystallize , there are two possibilities of forming mixed crystals with different water of hydration molecules depending upon the amount of each salt in the mixture since each substance brings its own influence, which may be made to predominate in turn according to the proportions of the mixture. When ‘a’ = 0.5 , ie when the both salts are in the same proportion by weight , the water molecules in each salt in the mixture is found to be same as they have in normal salt; in other words Copper Ammonium Sulphate has four water molecules and Zinc Ammonium Sulphate has six water molecules; ie., CuSO4.(NH4)2 SO4. 4H2O and ZnSO4.(NH4)2 SO4. 6H2O is the formula of the mixed crystal formed. When the values of a=0.909 , 0.833 and 0.7692 , the total water molecules in the mixture is found to be 8; ie ., as long as the weight of Copper Ammonium Sulphate in the mixture is higher, the water molecules in each salt in the mixture is found to be that of Copper Ammonium Sulphate , ie., 4H2O ,which is shown by the percentage of water lost in each experiment; in other words each salt has four water molecules ; now CuSO4.(NH4)2 SO4. 4H2O and ZnSO4.(NH4)2 SO4. 4H2O is the formula of the mixed crystal formed. When the values of ‘a’=0.3704 , 0.1667 and 0.100, the total water molecules in the mixture is found to be 12; ie ., as long as the weight of Zinc Ammonium Sulphate in the mixture is higher, the water molecules in each salt in the mixture is found to be that of Zinc Ammonium Sulphate , ie., 6H2O ,which is shown by the percentage of water lost in each experiment; in other words each salt has seven water molecules ; now CuSO4.(NH4)2 SO4. 6H2O and ZnSO4.(NH4)2 SO4. 6H2O is the formula of the mixed crystal formed. These results are clearly shown by the “ Table - 8” ; the values of ‘a’ slowly increases from 20.697 to 26.740 through the value 23.537 ; in other words the water molecules in the mixture goes on increase from Four to Six. These findings are based on the calculation of number of water molecules lost from the mixed crystals formed as given below: |
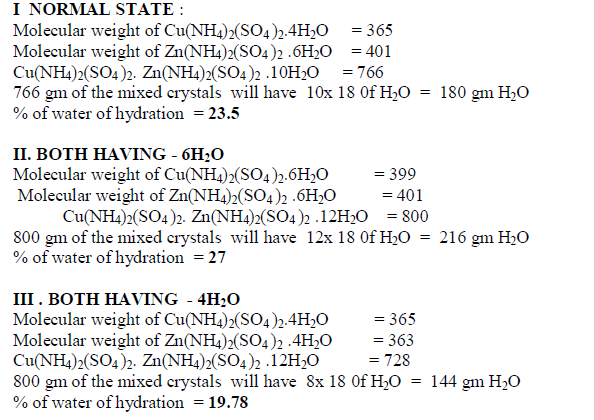 |
| The results prove that “ In a crystal containing a mixture of isomorphous substances, each substance brings its own influence, which may be made to predominate in turn according to the proportions of the mixture.” |
V.CONCLUSION |
| We have got mixed crystals of isomorphous salts with abnormal water of hydration. We know that the properties of hydrated water molecules depends on the number of water molecules also. The number of water molecules also play a vital role in the structure which in turn on the properties of the crystals. So the properties of Cu(NH4)2(SO4 )2.6H2O and Zn(NH4)2(SO4)2.4H2O will be definitely, at least to some extent , different from the molecules with the normal salts; if it is so, then those properties may be very useful and helpful to society. But we are unable to separate each crystal system; ie we did not separate Cu(NH4)2(SO4 )2.6H2O and Zn(NH4)2(SO4)2.4H2O and further, it is also not our aim and scope this Research work. If this work is taken by some Research Scholars and if they succeed to separate the crystals with the abnormal water of hydration , then it ,will make, I hope , wonderful changes in Crystal Field . |
References |
|