Laplace Transforms to KekreÃÂ¢Ãâ¬Ãâ¢s functions

H. B. Kekre; V. R. Lakshmi Gorty

Laplace Transforms to KekreÃÂ¢Ãâ¬Ãâ¢s functions

H. B. Kekre¹, V. R. Lakshmi Gorty²

Senior Professor, Department of Computer Science, SVKM’s NMIMS MPSTME, Mumbai, India
Associate Professor, Department of Computer Science, SVKM’s NMIMS MPSTME, Mumbai, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In this paper, the Kekre’s function is represented in mathematical concept. The Laplace transforms is applied to Kekre’s function and the results are obtained. The graphical representation is shown by MATLAB also to show the Kekre’s function. A generalized representation of Kekre’s function is shown in this paper. To all the assigned order N, of the Kekre’s functions, the solutions are displayed for each example. Linearity property using Laplace transforms when applied to Kekre’s function, is proved in the form of a theorem. For any positive arbitrary value, the transform of Kekre function is obtained and also shown how Kekre’s function is related to inverse Laplace transforms. At the end of examples, the generalized representation of the Laplace transforms of Kekre’s function is formulated.

Keywords

Kekre’s function, Laplace transforms, generalized representation, linearity property

INTRODUCTION

Kekre function is defined as

(1)

for any order, a = 0,1,2,3,...N and a < N.

Here N is the order of the Kekre’s function. Transform methods are typically used in many image processing applications such as compression, filtering, enhancement, feature extraction, image texture analysis etc. Using transform domain techniques, it is possible to embed a secret message in different frequency bands of the cover image. There are a number of linear transformations that prove useful in digital image processing. Most commonly used transforms are Discrete Cosine Transform (DCT), Discrete Sine Transform (DST), Walsh, Haar [15] etc. This paper proposes transforms applied to Kekre’s function [15] and can be used for various image processing applications. CBIR technology is implemented in a host of different applications which include art galleries, museums, archaeology [1],[2], architecture/engineering design [3], geographic information systems [5], weather forecast [4], medical imaging [4], trademark databases [6], criminal records [7], World Wide Web like photo sharing and video streaming sites[8]. Some of recent works on speaker identification depend on classical features including cepstrum with many variants [9], sub-band processing technique [10], Gaussian mixture models (GMM) [11], linear prediction coding [12], wavelet transform [13] and neural networks [14]. A lot of work in different applications to engineering fields has been done. But still there is lack of understanding of the mathematical interpretation using Kekre’s function is been observed. The author in the present study, proposes solution to some problems using Kekre’s function which will help further in application problems. In this paper, Kekre’s function is used to solve few problems using Laplace Transforms.

PRELIMINARY STUDY

Here the order of the Kekre’s function is ‘4’. Then the Kekre’s function can be represented as:

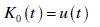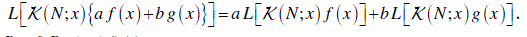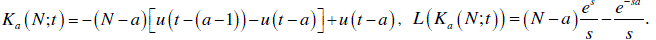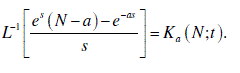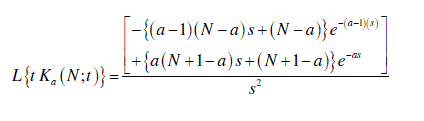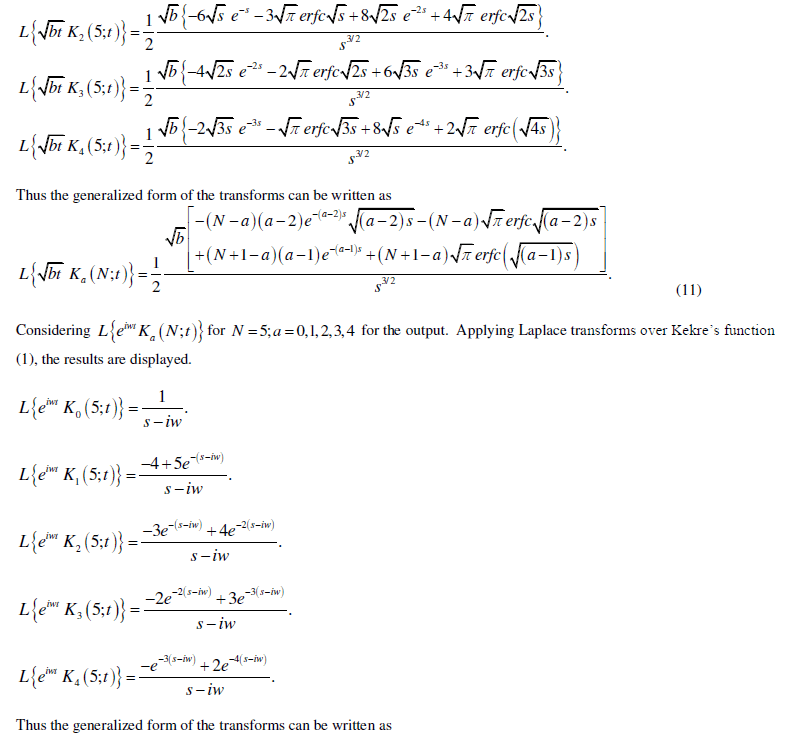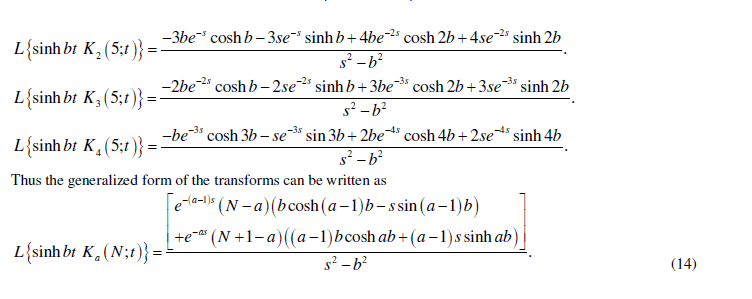RESULTS AND DISCUSSIONS

All the examples considering N = 4 or N = 5. These results can be calculated considering for any value of N . The results can be extended to complex variables. The real and imaginary parts of the function will be obtained. The formula can be proved in the similar manner. The elementary functions using Kekre’s function has been evaluated applying Laplace transforms over it. At the end of examples the generalized representation of the Laplace transforms of Kekre’s function is formulated.

CONCLUSION

Kekre’s function has been used in application to image processing and other computer engineering applications. This paper shows mathematical interpretation of Kekre’s function, such that even Mathematicians can use it efficiently. Results are displayed with their calculations and process of the existence of Kekre’s function.

FUTURE SCOPE

This evaluations and observation done by the author in this work can help researchers for the elaborate study in this direction. Evaluation and analysis can be done for higher orders. Continuous transforms of such functions can be studied. Applications to different fields of engineering can fulfill the introduction of such function and its mathematical concept. Table for all the Laplace transforms to Kekre’s function can be calculated.

References

N. Krishnan, M. Sheerin Banu, C. Callins Christiyana, “Content Based Image Retrieval using Dominant Color Identification Based on Foreground Objects”, In International Conference on Computational Intelligence and Multimedia Applications, 2007.
H. B. Kekre, Tanuja Sarode, Sudeep D. Thepade, “DCT Applied to Row Mean and Column Vectors in Fingerprint Identification”, In Proceedings of Int. Conf. on Computer Networks and Security (ICCNS), VIT, Pune, Sept. 2008.
H. B. Kekre, Sudeep D. Thepade, “Image Blending in Vista Creation using Kekre's LUV Color Space”, SPIT-IEEE Colloquium and Int. Conference, SPIT, Andheri, Mumbai, Feb 2008.
H. B. Kekre, Sudeep D. Thepade, “Boosting Block Truncation Coding using Kekre’s LUV Color Space for Image Retrieval”, WASET Int. Journal of Electrical, Computer and System Engineering (IJECSE), Vol.2, Num.3, Summer 2008. Available online at www.waset.org/ijecse/v2/v2-3-23.pdf.
Pengyu Liu, Kebin Jia, Zhuozheng Wang, Zhuoyi Lv, “A New and Effective Image Retrieval Method Based on Combined Features”, In Fourth International Conference on Image and Graphics, 2007.
H. B. Kekre, Sudeep D. Thepade, “Image Retrieval using Augmented Block Truncation Coding Techniques”, ACM Int. Conf. ICAC3-09, Mumbai (uploaded on ACM portal), Jan 2009
H. B. Kekre, Sudeep D. Thepade, “Using YUV Color Space to Hoist the Performance of Block Truncation Coding for Image Retrieval”, IEEE International Advanced Computing Conference 2009 (IACC’09), Thapar University, Patiala, INDIA, 6-7 March 2009.
H. B. Kekre, Sudeep D. Thepade, “Color Traits Transfer to Grayscale Images”, In Proc.of IEEE First International Conference on Emerging Trends in Engg. & Technology, (ICETET-08), G. H. Raisoni COE, Nagpur, INDIA, 2008.
Joseph P. Campbell, Jr., Senior Member, IEEE, “Speaker Recognition: A Tutorial”, Proceedings of the IEEE, vol. 85, no. 9, pp. 1437-1462, September 1997.
L. Besacier, J. F. Bonnastre and C. Fredouille, “Localization and Selection of Speaker-Specific Information with Statistical Modeling”, Speech Communications. 31: 89-106, 2000.
D. A. Reynolds, T. F. Quatieri and R. B. Dunn, “Speaker Verification Using Adapted Gaussian Mixture Models”, Digital Signal Processing. pp: 19-24, 2000.
Bassam A. Mustafa, B. Y. Thanoon and S. D. Al-Shamaa., “A Database System for Speaker Identification”, Proceedings of The 2nd International Conference on Information Technology, Al-Zaytoonah University of Jordan, May 2005.
L. Prina Ricotti, “Multitapering and Wavelet Variant of MFCC in Speech Recognition”, IEEE Proceedings on Vis. Image Signal Process., pp: 29- 35, 2005.
Z. Dokur, and T. Olmz, “Classification of Respiratory Sounds By using An Artificial Neural Networks”, International Journal of Pattern Recognition and artificial Intelligence. 4: 567-580, 2003.
H. B. Kekre, T. K. Sarode, Shachi J. Natu, Prachi J. Natu “Performance Comparison of Speaker Identification Using DCT, Walsh, Haar on Full and Row Mean of Spectrogram”, International Journal of Computer Applications (0975 – 8887) Volume 5– No.6, August 2010.