Keywords
|
| Non linear tank, Level process, PID controller, Control System |
INTRODUCTION
|
| Each and every industry phase the flow control and level control problem. So that canonical tank level process is used. Canonical tank level process is used. Canonical tank is the highly non-linear system. Because of this, reason sometimes output may be affected. Due to its shape, the conical tank is lead to non-linearity control of conical tank is the challenging problem so many researchers have been carried out in the level control of conical process. S. M. Giri Raj kumar, K. Ramkumar, Sanjay Sharma [1] explained Ants colony optimisation in level control of conical tank. N.S. Bhuvaneswari, G. Uma , T.R. Rangaswamy[2] carried out experiments in conical tank level control using Neural Network controllers. Swati Mohanty[3 ] designed Model Predictive Controller for floatation column . Artificial Neural Controllers are designed by Rahul Shridhar, Douglas. J. Cooper [4]. Unconstrained multivariable Tuning was proposed by R. Shridhar, D. J. Cooper [5]. The detailed description of designing MPC is explained by E. F. Camacho, Carlos Bordons[6].Conical Network modelling and multivariable Model Predictive tank is used in various process industries, food and packaging section, chemical industry, coal & mine industry and waste water management. |
| In process control industry, control of the level is very important one. Fluid level in the tank must be controlled. This is achieved by controlling the input flow into the tank. For maintaining the level in the tank, the inflow and outflow must be maintained. Proportional controller, which has more offset and error values more accuracy will not take place in this controller and take more time for settling. To reduce the offset in the process PI controller is used. It takes enormous time for achieving the set point. To reduce the time taken to reach the set point in process PID is used. PID used to reduce the oscillation, and eliminate the offset. In this tuning method, PID controller for different process based on dead time and the different order process with dead time. PID controller is common feedback controller component used for controller system. Anticipate the future error by the derivative action. In this work, control technique is deals with conical tank using Z-N tuning setting. Z-N gives better performance in tracking the set point and load changes with faster settling time. |
II. SYSTEM IDENTIFICATION
|
A. Modelling
|
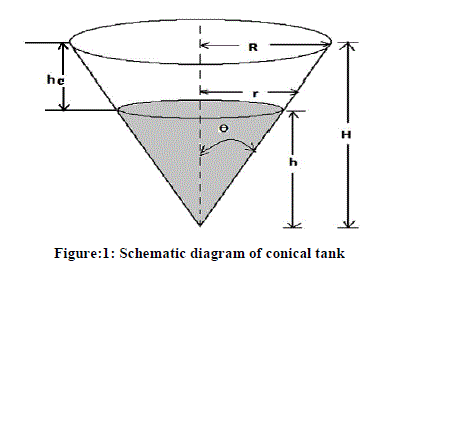
| Mathematical modelling is used to describe the process in mathematical manner. Here, mathematical model of the level process is shown in figure 1. |
The area of the conical tank is given by,  (1) (1) |
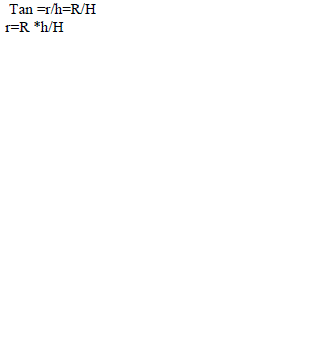 (2) (2) |
| According to law of conservation of mass, |
 |
 (4) (4) |
 (5) (5) |
| Where k is the discharge coefficient |
| Subs 5 in 4, we get |
 (6) (6) |
| Where, dh/dt-rate of change of height |
| Therefore, |
| A = (ïÃÂð * R² * h²)/H² |
| Substituting the value of A in equations, we get |
 (7) (7) |
| The above Equation describe the mathematical model for single conical tank level process, this equation is implemented in MATLAB Simulink. The basic method of identifying the system is step response method. A step change in inlet flow rate represents a process as first order transfer function with dead time. |
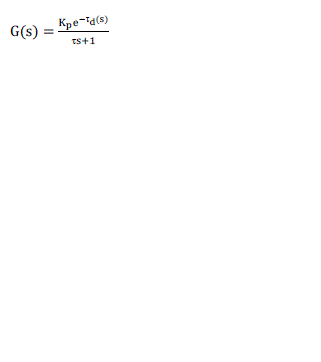 |
| Where K is the process gain; τ is the first order time constant; τd is the dead time |
III. CONTROLLER TUNING METHOD
|
| In this work, a conventional tuning is performed Ziegler-Nichols based PID controller setting and the performance is compared with CC and TL based PID controller. Specific tuning parameters are used for PIDcontroller. Some of the tuning methods are Ziegler Nichols method, and Tyreus-Luyben method, Cohn coon method. |
A.Ziegler Nichols Method
|
| This method was proposed by john G.ziegler and Nathaniel B.nichols. This popular method is frequency response analysis of the process; it is also known as ultimate gain method. Loop of this Ziegler Nichols closed loop.controlleris placed in this loop. By adjusting the gain of control system, ultimate gain (ku) can be measured and oscillation period also measured in terms of (pu) ultimate period. After measuring the ultimate gain and oscillation period values are noted. By using this ku,pu value -tr,ts,peak overshoot can be determined easily. |
B.Cohen –Coon Method
|
| In this method the process reaction curve is obtained first by applying an open loop test and then the process dynamics is approximated by a first order plus dead time model. This method is used when big delays are found in real time process. One of the disadvantage of Cohen - Coon method is that the resulting closed loop system is often more oscillatory than the desired signal. |
C.Tyreus Luyben’s Method
|
| It is similar to the Ziegler-Nichols method. The Tyreus and Luyben's tuning method Luyben and Luyben (1997) is based on oscillations as in theZiegler-Nichols' method, but with modified formulas for the controller parameters to obtain better stability |
IV. COMPARATIVE CONTROLLER ANALYSIS RESULTS
|
| Application and analysis of closed loop system is performed by implementing values available in table 5. PID controller setting values are calculated using the tuning formulas and values are shown in table 5. |
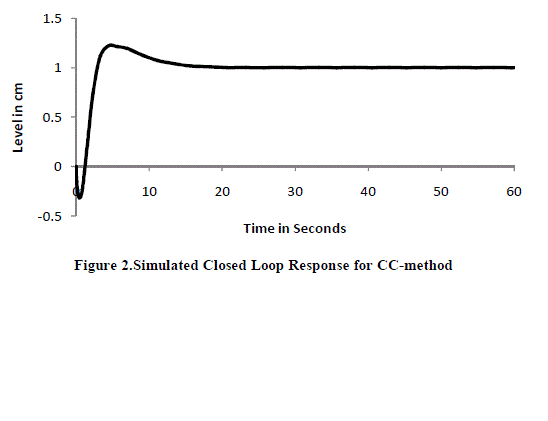
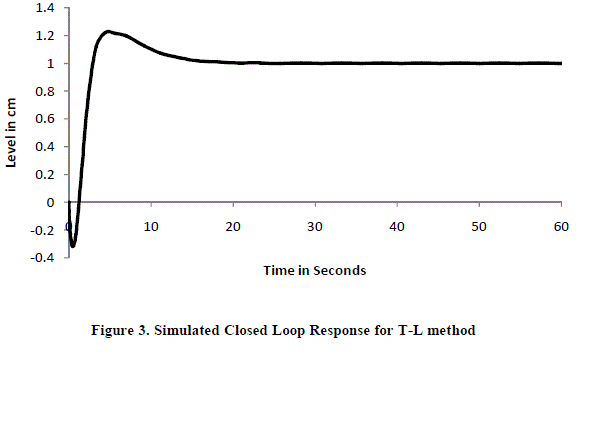
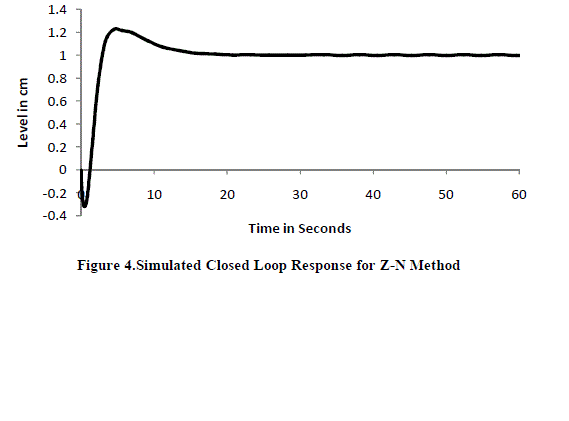
| By comparing these three methods closed loop response and time domain specifications of different controller settings are shown in figure 2, 3, 4 and table 6. Ziegler-Nichols based tuned PID controller settings method is identified as the best method based on time domain specifications. Because in this method the response get settled as soon as. That is these methods get less rising time and peak overshoot while compared to other two methods. |
V. CONCLUSION
|
| This paper has demonstrated a number of PID controller tuning methods being used to tune a Level controller for a nonlinear tank process. The obtained results confirmed that the Ziegler-Nichols method has less oscillation compared with T-L, C-C method and yield better response. The simulation responses for the model reveals the efficiency of the Ziegler-Nichols method in provision of time domain specifications by achieving minimum settling time and no overshoot. Hence from the above results it is concluded that Ziegler-Nichols method to be an improved choice for the Liquid level control of process tank than other PID controllers. |
Tables at a glance
|
|
|
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
| |
References
|
- S. M. GiriRajkumar, Dr. K. Ramkumar, Sanjay Sarma O.V," Real time application of Ants Colony Optimization," International Journal ofComputerApplications (0975 - 8887) Vol 3 - No.8, June 2010.
- N.S. Bhuvaneswari, G. Uma , T.R. Rangaswamy," Adaptive and optimal control of a non-linear process using Intelligent controllers," AppliedSoftComputing 9 , 182-190
- Swati Mohanty," Artificial neural network based system Identification and model predictive control of a flotation Column”, Journal of ProcessControl19 (2009),pp 991-999
- Rahul Shridhar, Douglas J.Cooper," A Novel Tuning For Multivariable MPC",ISA Transactions,vol - 36,No.4,pp 273- 280.
- Rahul Shridhar , Douglas J.Cooper," A Tuning Strategy for Unconstrained Multivariable MPC", Ind. Eng. Chern. Res. 1998, 37, 4003-4016.
- E. F. Camacho, Carlos Bordons “Model Predictive Control”2nd edition, Springer.
- P.Aravind, M.Valluvan, S.Ranganathan, “Modelling and Simulation of Non Linear Tank”, International Journal of Advanced Research inElectrical, Electronics and Instrumentation Engineering, Vol. 2, 2013.
|