Loss Based Distribution System Planning
Incorporating Multiple DG in Distribution Network

G.Ch; ra Prabha; S.Nagalakshmi

Loss Based Distribution System Planning Incorporating Multiple DG in Distribution Network

G.Chandra Prabha¹, S.Nagalakshmi²

PG Scholar, Dept. of EEE, Kamaraj College of Engineering and Technology, Virudhunagar, Tamil Nadu, India 1
Professor, Dept. of EEE, College of Engineering and Technology, Virudhunagar, Tamil Nadu, India 2

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Around the world, conventional power system is facing the problems of gradual depletion of fossil fuel resources, poor energy efficiency and environmental pollution. These problems have led to a new trend of generating power locally at distribution voltage level. This type of power generation is termed as distributed generation (DG) and the energy sources are termed as distributed energy resources (DERs).The distribution network becomes active with the integration of DG and hence is termed as active distribution network. DG provides several advantages such as reliability, flexibility and efficiency. Several optimization methods are utilized to find out the size and location of the DG with an objective of minimization of losses. In this paper, Differential Evolution Algorithm is used for optimal sizing and location with an objective of minimizing the power losses. The proposed method is tested on standard IEEE 33-bus test system and the results are tabulated.

Keywords

Differential Evolution (DE) algorithm, Distribution Power Flow (DPF), Distributed Generation (DG), Distribution Company (DISCO), Combined Heat and Power (CHP), Renewable Energy System (RES).

I.INTRODUCTION

The term "distributed generation" is used to refer to small-scale power generation devices that can be placed "on-site" at manufacturing plants. They range from a few KWs to a few MWs in size. DGs are located near load centres, so the transmission losses are minimized. Distributed generation allows collection of energy from many sources and gives lower environmental impacts and improved security of supply. Emerging new DG technologies include small, high efficiency internal combustion engines, mini and micro turbine generators, solar photovoltaic, wind turbine and fuel cells. Several optimization methods are utilized to find out the size and location of the DG corresponding to minimization of losses. Integration of renewable energy based distributed generation (DG) units provides potential benefits to conventional distribution systems.

II LITERATURE SURVEY

The power injections from renewable DG units located close to the load centres provide an opportunity for system voltage support, reduction in energy losses and emissions, and reliability improvement. Due to these and many other advantages, DG is expected to play a significant role in the power grid’s operation, structure, design, and upgrading planning [1]. Due to increase in penetration of DG the system is no longer passive and remains to be active [2]. A heuristic approach for DG investment planning is proposed [3] that aims to minimize the distribution company (DISCO)’s investment costs, operation costs and the costs related to system losses. It works by searching for a set of DGs that can have their marginal benefits greater than their overall installation and operation cost. In [4], analytical methods were proposed for multiple-DG placement to minimize system loss.In [5], genetic algorithm based optimization problem was proposed for loss minimization objective with an aim of increasing the profit of Disco.The optimal allocation of DG considering power losses of the system, as objective function is simulated using Monte Carlo Simulation (MCS) method using constriction factor based PSO algorithm [6]. In this paper, an optimization problem with an objective function of minimization of system losses in the distribution system incorporating multiple DG is solved using DE algorithm. The proposed work is simulated on standard IEEE 33-bus test system and results are tabulated.

III. DISTRIBUTED GENERATION

In traditional power system, the bulk of electricity is generated at central station generations and transmitted through a high- voltage transmission line to distribution networks before supplying to consumer loads. However, increase in load demand, technological innovation, environmental and aesthetic concerns and market liberalization lead to DG integration in distribution network. DG units can supply better quality of power, enhances voltage profile, and reduces congestion, reduces power losses and also delays the transmission and distribution network upgrade by making use of local resources. Based on the DG technology and the terminal characteristics, they can be classified into four types [10]:

Type 1) DG injects active power (P) only, e.g. Photo voltaic

Type 2) DG injects Reactive Power (Q) only, e.g., Synchronous compensator

Type 3) DG injects Active power but absorbs reactive power e.g. Induction Generator. The reactive power consumed by an induction generator in a simple form is given by

Type 4) DG injects both active and reactive power, e.g. Synchronous generators.

IV. OPTIMAL ALLOCATION ALGORITHM USING DIFFERENTIAL EVLOUTION

The classical DE algorithm consists of four steps namely initialization of population, mutation, crossover or recombination and selection (Storn 1997) [7],[8],[9].

(i) Initialization

DE searches for global optimum point in a D-dimensional real parameter space. The population members are randomly initialized using Equation (15).

If the trial vector yields an equal or lower value of fitness function, it replaces the corresponding target vector in next generation; otherwise the target vector is retained in the population. Hence, the population gets either better or remains the same in fitness status, but never deteriorates.

V.PROBLEM FORMULATION

The objective of the proposed optimization problem is to minimize the power losses in the system incorporating multiple DG in the distribution network. The objective function is given by,[6]

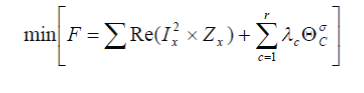Where

F- System Loss function

Ix – Branch Current

Zx- Branch Impedance

λc- Penalty function either (0 or 1)

ÃÂ¯ÃÂÃâ – penalty factor for constrain violation

The penalty factor will remove the non feasible solutions, which violate the system limits using penalty decision variable.

λC= 0 , if any constraint is violated and λC = 1, if all constraints are satisfied Subjected to ,

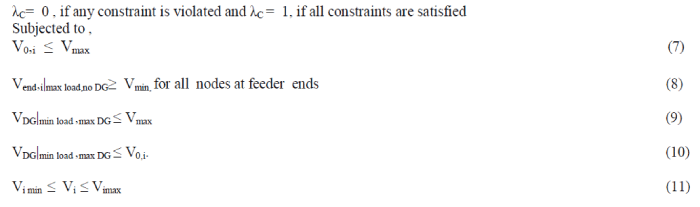The substation voltage is set to nominal (1.0 p.u.) throughout the optimization problem. In this optimal location and size of the DG is computed using DE algorithm. The proposed algorithm is tested with IEEE 33 bus distribution system[6].

VI. RESULTS AND DISCUSSION

The effect of DG in distribution system is tested for two types of DG namely, Type 1 and Type 4 DG. The penetration of DG is divided into two cases, single DG placement and multiple DG placements in distribution network. The parameters of DE algorithm used for two cases are tabulated in Table 1. For type 1 DG, the two variables are the size and location of DG and for type 4 DG, the three variables are the size, location and Power Factor of DG. The test system considered for testing is IEEE 33 bus distribution network is as shown in Figure 1.

CASE 1: LOSS REDUCTION INCORPORATING SINGLE DG PLACEMENT

In this case optimal location of single DG placement is carried out using DE algorithm. Maximum iteration considered is 200 and the size of DG considered ranges from 50 KW to 3 MW. This algorithm is tested for both type of

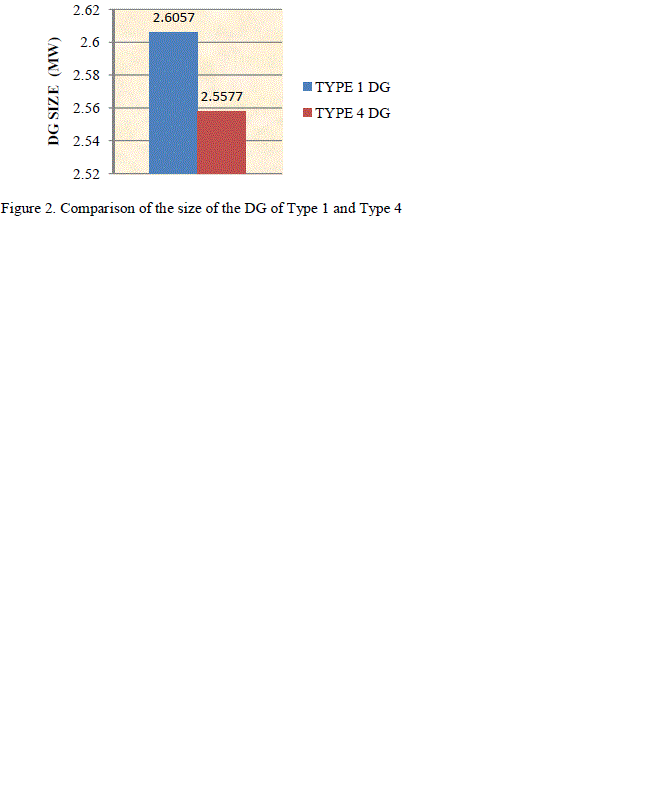
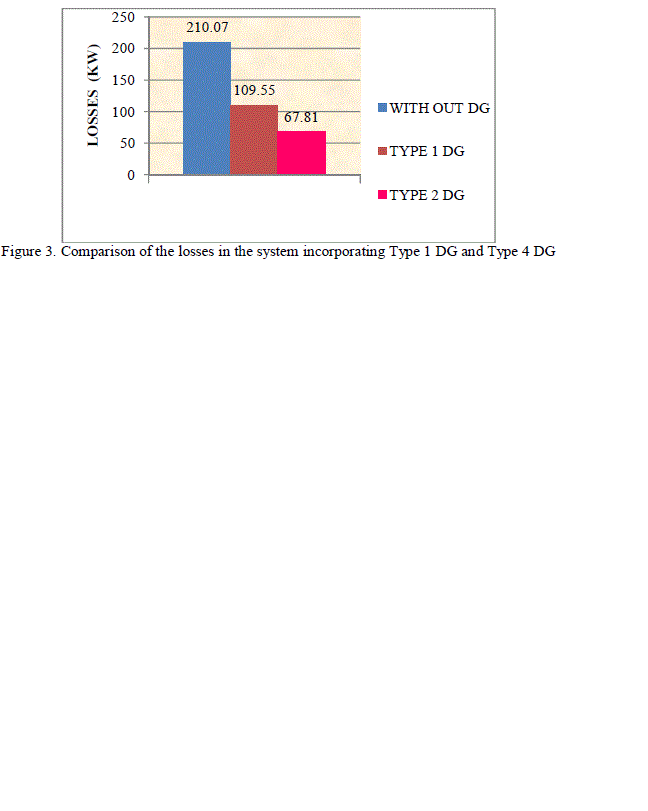
DG. When DG is of Type 1, only real power (P) support is rendered. The DG is considered as the negative load in the distribution system network, whereas in Type 4 DG both real power (P) and reactive power (Q) support is provided by the DG to the distribution network. The base case loss of the distribution network considered without incorporating DG is obtained as 210.07. Optimal DG size, location and corresponding losses of the DG obtained using DE algorithm is tabulated in the Table 2.When a DG size of 2.6057 MW of Type 1 is placed at bus number 6, losses of the distribution system reduces to half of the total losses without incorporating DG. When DG provides only the real power support (i.e. DG operating at UPF) the losses of the system reduces to 109.55 KW and the loss reduction is of 47.85%. When a DG size of 2.5577 of Type 4 is placed at bus number 6, losses of the system reduces to 67.8090 KW and the loss reduction is of 67.10%. The comparison of the size of the DG of Type 1 and Type 4 DG is as shown in Figure 2.

The comparison of the losses in the system incorporating Type 1 DG and Type 4 DG is as shown in Figure 3.

CASE 2: LOSS REDUCTION INCORPORATING TWO DG PLACEMENT

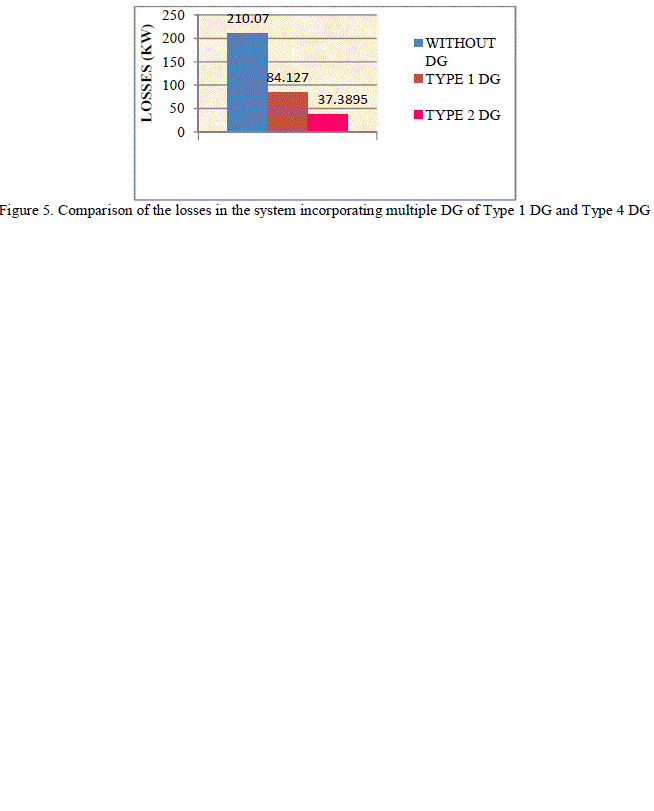
Instead of placing a single DG of larger size, multiple DG could be placed in more than one location of smaller sizes results in improved loss reduction. In this case the size of each DG is in the range of 50 KW to 1.5 MW. Optimal DG size, location and corresponding losses obtained using DE algorithm is as tabulated in Table 3. Optimal location and size of DG from DE algorithm is obtained as bus-13 and bus-30 of size 0.999 MW and 0.999 MW respectively. The loss in the system is reduced to 84.127 KW from base case loss of 210.07 KW by incorporating DGs in the distribution system and the loss reduction is about 59.95%. In case of Type 4 DG a much reduced loss of 37.3895 KW is obtained and the loss reduction is about 82.20%. The comparison of the size of the DG of Type 1 and Type 4 DG is as shown in Figure 4.The comparison of the losses in the system incorporating Type 1 DG and Type 4 DG is as shown in Figure 5.

CASE 3: LOSS REDUCTION INCORPORATING THREE DG PLACEMENT

The results of Two DG placements prove that distribution system losses reduce more in case of two DG placement than single DG placement. Hence, the results could be improved by incorporating more DG of lesser size. In this case three DGs are incorporated in the distribution system. The size range of each DG considered here is from 50 KW to 1MW. Optimal DG size, location and corresponding losses obtained using DE algorithm is as tabulated in Table 4. Optimal location and size of DG from DE algorithm is obtained as bus-13, bus-30 and bus-24 of size 0.899 MW, 1.1701 MW and 0.999 MW respectively. The loss in the system is reduced to 71.57 KW from base case loss of 210.07 KW by incorporating three DGs in the distribution system and the loss reduction is about 65.93% in Type 1 DG in case of Type DG a much reduced loss of 21.5922 KW is obtained as shown in Table 4. The comparison of the size of the DG of Type 1 and Type 4 DG is as shown in Figure 6.The comparison of the losses in the system incorporating Type 1 DG and Type 4 DG is as shown in Figure 7.

The results are compared with [6] and the overall comparison of the results obtained using proposed algorithm for Type 1 DG is as tabulated in Table 5 and the result for Type 4 DG is as tabulated in Table 6. The results prove that DE algorithm is very efficient for the objective function of loss reduction in the distribution system incorporating multiple DG in the distribution system and the obtained results are far better than the PSO based method suggested in [6].

VII. CONCLUSION

In this paper, an approach for Distribution system planning incorporating multiple DG considering system loss as objective is solved using DE algorithm. Optimal size, location and operating power factor is obtained from the DE algorithm. The results have been compared with Monte Carlo Simulation (MCS) method using constriction factor based PSO algorithm suggested in [6]. The results prove that DE is very efficient for loss reduction objective function incorporating multiple DGs. The system planning is done considering the DG technologies and their viability in the deregulated environment.

Tables at a glance


Table 1	Table 2	Table 3


Table 4	Table 5	Table 6

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4


Figure 5	Figure 6	Figure 7

References

R. C. Dugan, T. E. McDermott, and G. J. Ball, “Planning for distributed generation,” IEEE Ind. Appl. Mag., vol. 7, no. 2, pp. 80–88, Mar./Apr.2001

Griffin T, Tomsovic K, Secrest D, Law A. Placement of dispersed generation systems for reduced losses. In: Proceeding of IEEE 33rdannulHawaii international conference on systems sciences; 2000. p. 1–9.

D. Gautam and N. Mithulananthan, “Optimal dg placement in deregulated electricity market,” Elect. Power Syst. Res., vol. 77, no. 12, pp.1627–1636, 2007

D. Hung, N. Mithulananthan, and R. C. Bansal, “Multiple distributed generators placement in primary distribution networks for loss reduction,”1700 IEEE Transactions on Industrial Electronics, vol. 60, no. 4, april 2013.,

R. K. Singh and S. K. Goswami, “Optimum allocation of distributed generations based on nodal pricing for profit, loss reduction, and voltageimprovement including voltage rise issue,” Int. J. Elect. Power Energy Syst., vol. 32, no. 6, pp. 637–644, 2010

Jain .N, Singh .S.N, Srivastava S.C, “A Generalized Approach for DG Planning and Viability Analysis Under Market Scenario,” IEEETransactions on Industrial Electronics November 2013; volume 60 No 11.pp 5075-85.

K.V. Price, R. M. Storn, and J. A. Lampinen, Differential Evolution—A Practical Approach to Global Optimization. New York: Springer-Verlag Natural Computing Series, 2005

R. Storn, “On the usage of differential evolution for function optimization,” in Proc. Biennial Conf. North American Fuzzy InformationProcessing Society, Berkeley, CA, Jun. 1996

R. Storn and K. Price, Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization Over Continuous Spaces,International Computer Science Institute-TR-95-012, Mar. 1995

D. Hung, N. Mithulananthan , “Multiple Distributed Generator Placement in Primary Distribution Networks for Loss Reduction”, IEEETransactions On Industrial Electronics, Vol. 60, No. 4, April 2013.