Keywords
|
| Colour MRI and CT image compression, Curvelet transform, Lifting transform, Huffman coding, Decompression, Quality metrics parameters. |
INTRODUCTION
|
| Medical image diagnosis plays a vital role now days to save the life and cure diseases and thus usage of medical images have been drastically increased. Normally for the best quality medical images, spatial as well as colour resolutions are increased which consumes more bandwidth to store images. Emerging technological advancements to meet the memory requirements of day to day life seems not to fulfil the requirement of storage since data storage is proportionately increasing. Image compression is the ultimate solution to fulfil the storage requirements. Colour medical images such as Magnetic Resonance Images (MRI), Computed Tomography (CT) images, Ultrasound images, etc that result from radiological techniques capture volumic acquisitions of images that could be considered as succession of slices. Here any lapse in data leads to a big issue for surgical, diagnostic and telemedicine applications. So a heavy medical data accumulation is essential and this leads to the requirement of both effective lossless compression and efficient reconstruction algorithm. |
LITERATURE REVIEW
|
| Related works in the field of image compression from the recent literatures illustrate that the discrete wavelet transform, 3D integer wavelet transform[1], Daubechis wavelet transform and lifting wavelet transform in combination with the entropy encoding are used to compress medical images. These wavelet transforms are not so complex to compute but compression ratio is less. The lifting wavelet transform provides better results over other wavelet transforms [2]. The lifting transform in combination with the 1D-Daubechis wavelet transform provides a better compression ratio and bits per pixel value but tested only for the natural Images [3]. These combinations of transforms did not efficiently reconstruct the exact image after decompression process. Even though there is increased compression ratio but problem with diminishing quality of the original Image [4]. Medical images like MRI images are having large amount of details in the curved surfaces. The application of existing transforms was not able to reproduce proper information about these curved surfaces and edge information [5]. Huffman coding is a lossless coding technique and is also most suited in hybrid compression methods [6]. |
PROPOSED WORK
|
| In this paper, Curvelet transform with lifting scheme and Huffman encoding are used to compress medical images such as MRI brain and CT heart images as per the block diagram shown in Fig.1. These images are acquired and pre-processed using Weiner filter. Curvelet transform is applied over these pre-processed images. These are splitted into tiles and these tiles are resized to be grouped together and then added to get the resultant image. Further lifting is applied to the coefficients of the resultant Curvelet transformed images that results in high detailed low-low image. Then after the decomposition of medical images by Curvelet and lifting transform, Huffman encoding is used to compress. The parameters of compressed images are tabulated. The reconstruction of the medical images is done by applying the inverse lifting transform and inverse Curvelet transform and it matches with the original one.Figure.1 interprets the proposed methodology. |
| A. Curvelet transform |
| Curvelet transform was designed to represent edges and other singularities along curves much more efficiently than the traditional transforms using fewer coefficients with accuracy of reconstruction [7]. To represent an edge to squared error 1/N requires 1/N wavelets and only about 1/√N for Curvelets. Unlike the wavelet transform, it has directional parameter and the Curvelet pyramid contains elements with a very high degree of directional specificity [8], [9]. Among the two approaches of discrete Curvelet transform, wrapping method is faster and easier to implement than the UnequiSpaced Fast Fourier Transform (USFFT) method while having the same result as USFFT method [10]. |
| Hence wrapping method is employed in this work which assumes a regular rectangular grid to wrap the object. The idea is to first decompose the image into a set of frequency bands and to analyse each band by a Curvelet transform. The block size can be changed at each scale level. The discrete Curvelet transform is applied as splitting the image into three primary colour bands (i.e., Red, Green, and Blue) as shown in Fig.3,4 and 5 respectively and for each colour band the following wrapping algorithm is applied. |
| • Compute the Fast Fourier Transform(FFT) of the image |
| • Divide FFT into collection of digital tiles |
| • For each tile |
| (a) Translate the tile to the origin |
| (b) Wrap the parallelogram shaped support of the tile around a rectangle centered at the origin. |
| (c) Take the inverse FFT of the wrapped support. Add the Curvelet array to the collection of Curvelet coefficients as shown in Fig.5. |
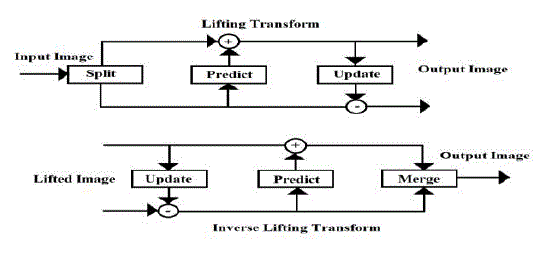
| B. Lifting wavelet transform |
| Lifting scheme as shown in Fig.6 is a rather new method for constructing wavelets [1]. The main difference with the classical constructions is that it does not rely on the Fourier Transform. In this way, lifting can be used to construct secondgeneration wavelets. The basic idea behind the lifting scheme is the usage of correlation in the data to remove redundancy. |
| In split phase, the data is split into odd samples and even samples. N even samples are used to predict the value of neighbouring odd value in predict phase. This updates the even samples using the newly calculated odd samples such that the desired property is preserved. |
Splitting: (3) (3) |
| Π – Total samples of input data; S – Even Samples of input data; d – Odd Samples of input data |
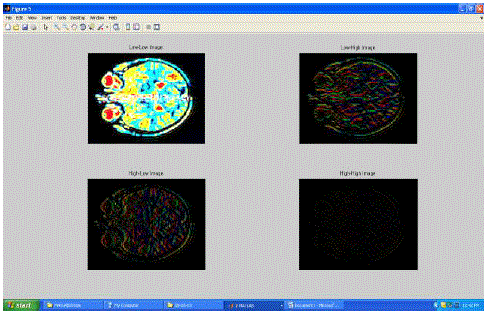
| Fig.7 shows one of the lifted images which has low-low, low-high, high-low and high-high images and it is evident that low-low image has high details. |
STEPS IN MRI AND CT IMAGE COMPRESSION
|
| • Acquisition of medical images and pre-process by using median and Wiener filters |
| • Applying Curvelet transform to the pre-processed images and decomposing them. |
| • Performing lifting scheme and extracting the high detailed Low-Low image. |
| • Applying Huffman coding to compress images. |
| • The reconstruction of the image is done by performing inverse lifting and Curvelet transforms |
| • Compression ratio and other quality metrics parameters are computed using appropriate formulae. |
| Inverse wrapping algorithm: |
| • For each Curvelet coefficient array |
| (a) Take FFT of the array |
| (b) Unwrap the rectangular support to the original shape. |
| (c) Translate to the original position |
| (d) Store the translated array |
| • Add all the translated Curvelet arrays |
| • Take the inverse FFT to reconstruct the image |
QUALITY METRICS
|
| A. Mean square error |
| In the image coding, the most frequently used measures are deviations between the original and coded images of which the mean square error (MSE) or signal to noise ratio (SNR) being the most common measures. The effectiveness of the coder is optimised by having minimum MSE. |
 ( 4) ( 4) |
| B. Peak signal to noise ratio |
| Larger PSNR indicate a smaller difference between the original (without noise) and compressed image. This is the most widely used objective image quality or distortion measure. The main advantage of this measure is ease of computation but it does not reflect perceptual quality. |
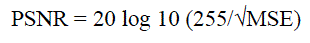 (5) (5) |
| C. Structural Correlation |
| Structural correlation (SC) estimates the similarity of the structure of two signals. This measure effectively compares the total weight of an original signal to that of a coded or given. A large value of structural correlation means that the image is of poor quality. |
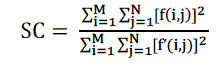 (6) (6) |
| D. Normalised Correlation |
| The closeness between two digital images can also be quantified in terms of Normalized Correlation (NK) function. These measures measure the similarity between two images, hence in this sense they are complementary to the difference based measures. |
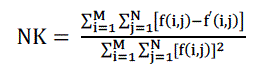 (7) (7) |
| E. Average difference |
| A lower value of Average Difference (AD) gives a cleaner image as more noise is reduced and it is computed as |
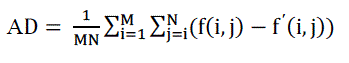 ( 8) ( 8) |
RESULTS AND DISCUSSIONS
|
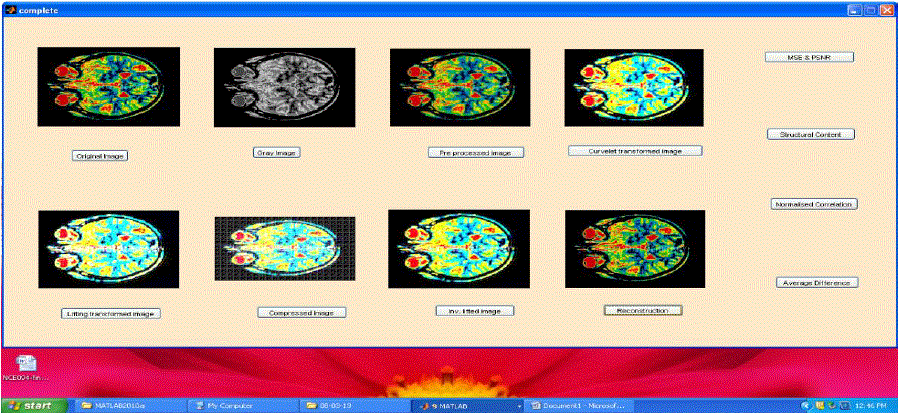
| The transformation is performed on CT and MRI images with varying pixel sizes and obtained from various portions of the body. Compression ratio (CR) is computed from the ratio of original file size to the length of output bit stream and Bits per Pixel (BPP) is also calculated. Fig. 8 show the snapshots of MRI brain image compression and decompression processes and quality metrics parameters. They show the original image acquired, gray converted, pre-processed image, curvelet transformed image, lifted one, compressed image, inverse lifted and decompressed image. MSE and PSNR, SC, NK and AD are computed and displayed in the window by clicking the corresponding bar shown in figures 8. The results are tabulated in Tables 1, 2 and 3. |
| • As per the Table.1, Compression ratio is improved much than the existing methods for colour medical images. Bits per pixel value are less than two and it ensures optimum storage requirement. The PSNR value is around 70% and it seems to be better than the existing values. |
| • Table.2 reveals that the Structural content is less than one and seems to be optimum. Normalized Correlation is also very close to one which shows the similarity between original image and reconstructed image. |
| • As per the Table.3, MSE with mean of 0.08 is within acceptable limit. Average difference shows minimum value and ensures high quality. |
SUMMARY AND CONCLUSION
|
| Thus colour medical image compression by Curvelet transform with lifting and Huffmann coding alleviate memory problem by increasing the compression ratio without degrading its original quality. It works well for variety of images with different sizes. The proposed method gives higher compression ratio when compared to other compression schemes with perfect post reconstruction quality. It finds applications in telemetry and telemedicine. |
Tables at a glance
|
|
|
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
Figure 8 |
|
| |
References
|
- Victor Sanchez, Rafeef Abugharbieh and Panos Nasiopoulos:”3-D Scalable Medical Image Compression with Optimized volume of Interest coding”- IEEE Transactions on Medical Imaging, Oct 2010. Vol.29 NO.10.
- Aree A.Mohammad and Loay E.George: “Intraframe Compression Using Lifting Scheme Wavelet-Based Transformation (9/7-Tap Filter)”- Journal of Zankoy, Sulaimani, Dec 2008.
- V.S.Vora, Prof. A.C.Suthar, Y.N.Makwana and S.J.Davda: “Analysis of Compression Image Quality Assessments” – International journal of Advanced Engineering and Applications, Jan 2010.
- Jonathan Taquet,Claude Labit, “Optimized decomposition basis using Lanczos filters for lossless compression of biomedical images” – IEEE Transactions on Biomedical Engineering, Oct 2010.
- Emmanuel Candes, Laurent Demanet, David Donoho and Lexing Ying: “Fast Discrete Curvelet Transforms”-Mar 2006.
- Dr.Y.Venkataramani,S.ParveenBanu:“AnEfficient Hybrid Image Compression Scheme based on Correlation of Pixels for Storage and transmission of Images”-International Journal of Computer Applications , Mar 2011.Vol 18,No.3.
- Truong T. Nguyen and Herve Chauris : “Uniform Discrete Curvelet Transform”- IEEE Transactions on Signal Processing, July 2010, Vol. 58, NO.
- Mohammad Saleh Miri, Ali Mahloojifar: “Retinal Image Analysis using Curvelet Transform and Multistructure Elements Morphology by Reconstruction” – IEEE Transactions on Biomedical Engineering, May 2011,Vol. 58 No.5 (1183-1192)
- D. L. Donoho and M. R. Duncan: “Digital Curvelet transform- Strategy, implementation and experiments”, Proc SPIE, 2000,vol. 4056, pp. 12–29
- Yuancheng Li, Qiu Yang, Runhai Jiao: “A Novel Image Compression Algorithm using the Second Generation of Curvelet Transform and SVM” –Global Congress on Intelligent Systems-IEEE Computer Society, Nov. 2009. (117-125)
- Nishat Kanvel. T.M.T., and DR. Elwin Chandra Monie: “Performance Measure of Different Wavelets for A Shuffled Image Compression Scheme”, International Journal of Computer Science and Network Security ,Mar. 2009, 215-221.
|